コンピュータの基礎第4講
種々の内部表現
【第4講のポイント】
前項では、整数データの内部表現について学んだ。では、その他の様々なデータをコンピュータ内部ではどのように表現しているのだろうか。本講では、同じデータでも解釈によって内部表現が異なること、そして、整数以外の小数点数(倍精度実数)・文(文字列)・画像・音声の内部表現について学ぶ。
【第4講の目標】学習後、以下のことが身についたかチェックしよう。
- 同じデータに対する解釈による内部表現の違いを理解する
- 小数点数の内部表現を理解し、近似計算にともなう誤算について理解する
- 16進数が扱える
- 文字の内部表現を理解し、整数と同じように扱えることを理解する
- 画像のデジタル化および非圧縮形式の符号化(内部表現)について理解する
- 動画のデジタル化法と圧縮の必要性について理解する
- 音声のデジタル化および非圧縮形式の符号化(内部表現)について理解する
- 標本化定理について理解する
【第4講の構成】
- 解釈による内部表現の違い
- 小数点数の内部表現
- 16進数
- 文字の内部表現
- 画像(フルカラー)と動画
- AD変換と音声
第1節 解釈による内部表現の違い
以下の欄でデータは解釈によってその内部表現が異なることを確認しよう。コンピュータでの内部表現の違いは処理や計算結果の違いにつながるので、そのことを理解・意識することが大切である。
|
第2節 実数の内部表現
実数は一般に無限の桁数を持ち、完全なモデルを作ることは不可能だから、0.31415926×1011 のような、仮数部×基数指数部 の形の浮動小数点数として近似表現される。コンピュータに10進浮動小数点形式で入力する際は、例えば 0.31415926e11 のように 仮数部e指数部(仮数部E指数部)の形で表す。(以下簡単のために、基数=10 の 10進表現で説明するが、コンピュータ内部では 基数=2 の 2進浮動小数点数である。)
計算は仮数部の有効桁数内での近似計算になるので、誤差が避けられない。通常は 64ビットの倍精度浮動小数点数が使われ、仮数部の有効桁数は 10進 15~16桁(2進52桁)である。以下の浮動小数点電卓で実験しよう。
|
1.のように、2進表現で無限(循環)小数を有限桁で丸めることから生じる誤差を丸め誤差という。分数(有理数)が無限(循環)少数になるか否かは基数によって異なり、10進数の 0.1 は2進数では無限小数 0.000110011… である。
一方、3.では、(相対的に)大きな小数点数に小さな小数点数を加えても値は増えない(正しく計算できない)。相対的に小さな値の情報が無視されてしまうことから、これを情報落ちという。
| コラム.足し算は順番で結果が異なる? |
|
an=8/(1×3)+8/(5×7)+8/(9×11)+…+8/((4n-3)(4n-1)) と bn=8/((4n-3)(4n-1))+8/((4n-7)(4n-5))+…+8/(1×3) とは 足し算の順番が異なるだけで数学的には等しく、n を大きくするとともに円周率πに収束する。しかしコンピュータでは計算結果が異なる。 右のアプリで n=60000000, 80000000, 100000000 での計算結果を求めて比較せよ。 8/((4k-3)(4k-1)) の値を大きい順に(kの値の小さい順に)加えた an で計算したπの値は、n の値がある程度以上になると情報落ちが生じるため、精度が上がらない(値が一定になってしまう)。 この例のように非常に多くの数の和を求める際は、(絶対値の)小さな数から順に加える等の工夫が必要になる。 |
第3節 16進数
| 2進 | 10進 | 16進 |
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
1×162+4×16+11=256+64+11=331
あるいは
(1×16+4)×16+11=331
である。
逆に10進数を16進数に変換するには、2進数のときと同様に、16 で割った余りを求めることを繰り返し、得られた余りを逆順に並べればよい。
計算例
16)331
16) 20 … 11(B)
16) 1 … 4
0 … 1↑ 答.14B
一方、16=24 なので、16進法は右表のように2進4桁( 4 ビット)をまとめて 1 文字で表す
ために使われることも多い。その場合対応する2進表示では、頭の 0 を消さず、4桁ごとに区切りの空白をいれて表示する。次節以降の内部表現の記述には、この意味で16進数表示が用いられる。
例.16進数 5A ⇔ 2進数 0101 1010
|
第4節 文字の内部表現
英数字(半角文字)は 1バイト(8ビット)のASCII符号で、漢字やひらがな(全角文字)は 2バイト(16ビット)のシフトJIS符号で符号化されることが標準的であったが、最近は世界中のすべての文字を(2バイト以上の)複数バイトで符号化するユニコードが普及している。絵文字😂🎄・・・もコード化され、アプリが対応していれば表示される。文字の表現に使われている符号を誤認すれば 文字化けを起こす。このページを表示しているブラウザで「文字エンコーディング」を変更してみよ。
|
| 実習.文字と整数の関係(C言語) |
paiza.ioのサイトを開き、4行目(カーソル位置)に次の命令を入力し【実行】してみよう
|
第5節 画像(フルカラー)と動画
画像は、格子状の細かなドット(ピクセル、画素)ごとに光の3原色(RGB)それぞれの輝度(明るさ)を1バイト(0~255)で指定することによって内部表現される。右のカラーパレットで代表的な色(赤、青、緑、黄、紫、白、黒、…)とRGB値の関係を調べよ。
例.(横)800×(縦)600画素の(非圧縮)画像のデータ量は 800×600×3=1,440,000B=1.44MB(メガバイト) になる。
動画
動画は、毎秒30枚程度の画像を、音声データと同期をとって連続的に表示させ、残像効果により動いているように見せている。毎秒の画像の表示枚数を fps (Frames Per Second)で表す。参考:愛知県総合教育センター教科情報 生徒実習課題例の動画の仕組み
|
この問からもわかるように、画像や動画(音声)のデータ量は圧縮しないと膨大になる。圧縮については次講で解説する。
第6節 AD変換と音声
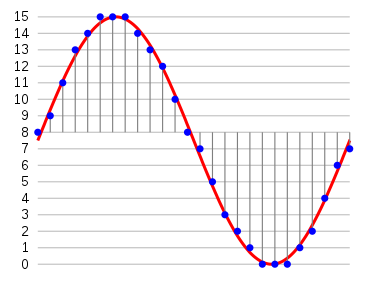
音波のAD変換(Wikipedia)
AD変換
画像や音声のような本来連続的なアナログデータを、コンピュータで扱える離散的なデジタルデータに変換することをAD変換という。AD変換の手順は、標本化、量子化、符号化の3段階に分かれる。- 標本化
- アナログデータを細かな区間に分けて、それぞれの区間での値(標本値)をとる。画像ではドット(画素)ごとの色をとることが、CD音楽では(約)44KHzで(1/44000秒ごとに)波形の高さをとることが、標本化にあたる。標本値は基本的に連続量である。
- 量子化
- 標本化で得た標本値を、あらかじめ定められたレベルに分けて離散数値(量子値)化する。カラー画像では光の3原色ごとに各々256段階に、CD音楽では 65536=216 段階に量子化している。
- 符号化
- 量子値を0,1の列で表す。カラー画像の量子値(色)は3バイト、CD音楽の量子値は2バイトの符号で表される。
| コラム.単純なAD変換 |
|
画像や音声を例にとってAD変換の手順を説明したが、長さを物差しで測り目盛を読む(というAD変換の)場合、標本化は無く直接量子化していることになる。水銀体温計の場合、体温というアナログデータ(情報)を水銀柱の長さというアナログデータで表し、目盛を読取るという量子化を行っている。 一般的に言えば、連続関数 y=f(x) のAD変換(離散化)において、(独立)変数 xの離散化を標本化といい、(従属)変数 yの離散化を量子化という。 |
| 1時間分のステレオ音楽のCDデータを、44KHzで標本化し、標本値を2バイトで符号化(量子化)するとき、何バイトになるか。 |
標本化定理
標本化周波数(単位あたりの標本数)の1/2の周波数(未満)までを忠実に再現できる(もとにもどせる)。人の可聴域が20Hzから20000Hz程度であることから、音楽CDの標本化周波数を44100Hz(≧2×20000Hz)にしている。 音のデジタル化(愛知県総合教育センター教科情報 生徒実習課題例)を参考にせよ。
| 音楽CDの標本化周波数が44.1KHzである理由を述べよ |
| コラム.ベクタ形式とMIDI |
| 画像や音声にはここで説明したのとは別の表現がある。 |