コンピュータの基礎第10講
データファイル
【第10講のポイント】
問題を解く手順(解法)をアルゴリズムといい、その手順をコンピュータ上で実現したものをプログラムという。本講では、データファイルに対するレコードの編成法と探索、追加、削除アルゴリズムについて学ぶ。 その準備としてまず、アルゴリズム(プログラム)の巧拙によって、計算時間(やメモリー量等)が大きく異なることを学ぶ。問題を解決するための効率のよいアルゴリズムを開発することはコンピュータサイエンスの重要な課題である。
【第10講の目標】学習後、以下のことが身についたかチェックしよう。
- アルゴリズムの巧拙によって、計算時間の大きな差が出ることを理解する
- 計算時間を見積もる原理がわかる
- 順編成アルゴリズムを理解している
- 整列順編成アルゴリズムを理解している
- 直接編成アルゴリズムを理解している
- 索引順編成アルゴリズムを理解している
- 2分探索木についてしている
【第10講の構成】
- アルゴリズムの巧拙
- データベースファイル
- 順編成アルゴリズム
- 整列順編成アルゴリズム
- 直接編成アルゴリズム
- 索引順編成アルゴリズム
- 2分探索木アルゴリズム
第1節 アルゴリズムの巧拙
問題を解く手順(解法)をアルゴリズムといい、その手順をコンピュータ上で実現したものをプログラムという。アルゴリズム(プログラム)の評価には、分かりやすさ(単純さ)、計算時間、使用メモリー量等の基準が考えられる。本節では、アルゴリズムの巧拙で計算時間に大きな差ができることを体験的に学ぶとともに、その評価で重要な働きをするオーダーの概念を理解する。オーダー
アルゴリズムの計算時間をどのようにの評価すればよいだろうか。アルゴリズムを実装したプログラムの実際の計算時間は、使用したプログラミング言語によって異なるし、実行するコンピュータ(さらには実行時の環境)によっても異なるので現実的ではない。さらにそもそも、計算時間は入力データのサイズによって異なる。手がかりとなるのは、適切な演算を指標にして、その実行回数を数えることである。指標としてどの演算を選ぶかは問題(アルゴリズム)によって異なるが、適切に選べば計算時間がその実行回数に比例するようにできる。そして、演算の実行回数を入力サイズの関数として表すことができれば、次ページの表のように、小さなサイズのサンプル入力に対する計算時間から、実際の入力(サイズ)での計算時間を見積もることができる。
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
計算時間の増え方や基準サイズの計算時間の何倍になるかを問題にする立場では、例えばサイズnの入力に対する演算回数が 2n2+5n であるとき、nがある程度大きくなると、5nの項はn2に比べて無視できるし、n2の係数2も無関係である。このとき、 2n2+5n のオーダーは n2 であるという。
このように、(1変数)関数がいくつかの項の和で表されているときに、(変数の増加に伴う)増え方のもっとも大きな項を取り出し、その定数係数を無視したものを、その関数のオーダーという。
|
ベキ乗計算アルゴリズム
yのx乗(yx)の素朴な計算法は、y, y2,y3, ・・・, yx, とyを順に掛けていく方法であろう。この方法では、(x-1)回の掛け算が必要だから、その計算にはオーダー x の時間がかかり、桁数が1増えると10倍の時間がかかる。一方Binary法と呼ばれる高速計算法では、yxの計算に、xの2進表示と、y1, y2, y4, y8,… の値を利用する。例えば15の2進表示は1111なので、y15=y8+4+2+1=y8・y4・y2・y1である。このとき、y2, y4, y8 の計算は2乗計算の繰り返しで掛け算3回、 さらに、y8・y4・y2・y1の計算が掛け算3回でできる。y22ならば、22は2進5桁の10110なので、y22=y16+4+2=y16・y4・y2である。このとき、y2, y4, y8, y16 の計算は2乗計算の繰り返しで掛け算4回、さらに、y16・y4・y2の計算が掛け算2回なので、計6回の掛け算でできる。
この方法での yx の計算は、xが2進k桁のとき、y1, y2, y4, … y2k-1の系列を計算するのに掛け算 k-1回、これらを組み合わせてyxを計算するのに(最大) k-1 回の掛け算、都合、2k-2回の掛け算で計算できる。そのオーダーは log2 x であり、素朴な計算法に比べて圧倒的に速い(オーダーの表を参照せよ)。
|
注意.電卓に入力するとき3ケタ毎の区切りのカンマは入力しない。 MOD電卓では、MOD欄の値で割った余り(上の場合下7桁)が表示される。
|
整列(ソーティング)
整列(ソーティング)は、データを大きさの順に並べ替えることで、表計算やデータベース管理システムにも基本機能として実装されている。ここでは直観的に理解しやすい選択ソートと、高速整列法として知られるクイックソートについて、基本的なアイディアと計算時間について体験的に理解しよう。
(他の整列法も実験できる。興味のある人は試してみよう。)
選択ソートでは、
未整列部(赤字)から最大値を選択してその右端に移動させる(青字)
ということを繰り返す。計算時間は、デモ表示される赤字の個数に比例するから、オーダーn2である。これはデータ数が2倍になると計算時間がほぼ4倍になり、データ数が10倍になれば計算時間がほぼ100倍になることを意味する(オーダーの表を参照せよ)。
クイックソートは、
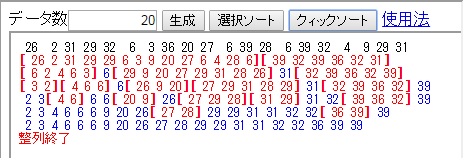
クイックソートの計算時間は分割にかかる時間(赤字数)の総和で、その評価は(入力データによって異なり)実は難しいが、平均してオーダー n・log2n であることが知られており、データ数が10倍になるとほぼ10倍になる(オーダーの表を参照せよ)。
未整列部([赤字])の右端の値を基準に、基準値以下の未整列部分([赤字])と基準値以上の未整列部([赤字])に分割する
ということを繰り返す。
クイックソートの計算時間は分割にかかる時間(赤字数)の総和で、その評価は(入力データによって異なり)実は難しいが、平均してオーダー n・log2n であることが知られており、データ数が10倍になるとほぼ10倍になる(オーダーの表を参照せよ)。
注意.①データ数を入力するときは、3ケタ毎の区切りのカンマは入力してはいけない。②整列の前に、必ず【生成】ボタンでランダムなデータを生成しておく。
|
第2節 データファイル
データファイルはレコードの集まりで、レコードは各フィールド(項目)に対する値の組である。通常、レコードが持つフィールドは一定で、キーフィールドと呼ばれるその値からレコードが一意に定まるフィールドを持つ。| フィールド名 | 【番号】 | 【氏名】 | 【住所】 |
| レコード | 001 | 青森健太 | 青森県青森市… |
| 002 | 宮城遼 | 宮城県仙台市… | |
| 003 | 長野愛子 | 長野県長野市… | |
| … | … | … |
データファイルに対する基本的な操作はレコードの探索・追加・削除で、キーフィールドはその際の手がかりとなるフィールドである。これらの操作を効率よく行うために、様々な編成法が考案されている。以下の節で基本的なファイル編成法について学ぶ。以下、簡単のため、レコードはキー値のみとし、レコードの追加で重複のチェックは行わないものとする。
次の表は、これから学ぶ編成法の計算時間(ステップ数)である。これを見ると直接編成が一番効率が良いが、後で見るように、特別な条件のもとでしか成立しない。
(レコード数N=1,000,000の時の平均ステップ数)
1は定数ステップの意味なので、+1はステップ数としての意味はない
(レコード数N=1,000,000の時の平均ステップ数)
| 編成法 | 探索 | 追加 | 削除 | 備考 |
| 順編成 | N/2 (500,000) | 1 | N/2+1 (500,000+1) | |
| 整列順編成 | log2N (20) | N/2 (500,000) | log2N+N/2 (20+500,000) | |
| 直接編成 | 1 | 1 | 1 | 衝突が生じない場合 |
| 索引順編成 | 1+N/M/2 (1+500) | 1+1 | 1+N/M/2 (1+500) |
ブロック数M=1,000とした。 |
| 2分探索木 | log2N (20) | log2N+1 (20+1) | log2N+1 (20+1) |
第3節 順編成アルゴリズム
順編成はレコード(データ)を単に1列にならべて管理する(Nはレコード数)。探索:頭から順に探す。(順探索)
追加:レコード列の最後に追加する。
削除:削除レコードを順探索し、削除後、最後のデータをそこに移す。
以下のアプリでは【生成】ボタンでレコードを生成し、レコード欄に指定されたデータの【探索】【追加】【削除】過程が表示される。
注.デモで、操作のステップ数は赤字の個数に等しい
| 探索、追加、削除にかかる(平均あるいは最悪の)ステップ数を示し、理由を説明せよ。 |
第4節 整列順編成アルゴリズム
整列順編成はレコード(データ)をキーで整列して管理する(Nはレコード数)。探索:2分探索法
探索範囲の中央値(赤字)と比べて、
小さければ前半を、大きければ後半を新たな探索範囲(青字)とする
ということを繰り返す
削除: レコードを2分探索し削除後、後のデータを順に詰める
追加: より大きなレコードを後にずらしながら、挿入場所を探す。
注.デモで、操作のステップ数は赤字の個数に等しい
| 探索、追加、削除にかかる(平均あるいは最悪の)ステップ数を示し、理由を説明せよ。 |
第5節 直接編成アルゴリズム
直接編成は、ハッシュ関数と呼ばれる、キーの値からレコードの格納位置(番地)を直接計算する関数を利用する。キーの値 ⇒【ハッシュ関数】⇒ レコードの格納位置
ハッシュ関数があれば、探索、追加、削除は、格納位置が(関数計算の)1ステップでわかり、そこで存在確認・追加・削除を行うだけなので、全体でも1(定数)ステップですむ。
例.学生ファイル
2016年入学生(300名以下)の学生番号が2016001~2016300ならば、ハッシュ関数をh(n)=n-2016000とし、レコードを1~300の番地(位置)に置けば、学生番号から直接(1ステップで)レコードの格納位置がわかる。
適当なハッシュ関数があるとは限らない
最初に注意すべきは、キー値の候補数はレコード格納番地数に比べ、通常莫大なことである。上の例でも、これまで入学した全学生を対象に学生番号をそのままレコード番地(h(n)=n)にしたら、番地のほとんどにレコードが存在しないことになって、現実的でない。10文字の英数字(26+10=36通り)からなるユーザIDをキーとする場合であれば、キーの候補数は3610≒3656兆となり、ユーザ数が3656人ならその1兆倍である。さらに、学生番号と違って、実際のレコードの分布が、あらかじめ(探索せずに)わかるということはないだろう。
したがって、通常、ハッシュ関数は、異なるキー(の候補値)に対し、同じ値を割り当てることになる。すると、現実に存在するレコード(のキー値)にハッシュ関数が同じ値を割り当ててしまうこと(衝突)が避けられない。そして、衝突が避けられなければ直接編成法は使えない。
その解決策が、次節で述べる索引順編成である。
| コラム.ハッシュという言葉の意味 |
| ハッシュ(hash)は、本来(肉を)切り刻むという意味で、ハヤシライスのハヤシ(hashed beef)の語源でもある。ハッシュ関数は、衝突をさけるため、単純な関数ではなく、もとのキー値を分解した(切り刻んだ)各部分が関数値に影響するように作る必要があることから付けられた名前である。 |
第6節 索引順編成アルゴリズム
索引順編成は、ハッシュ関数(直接編成)における衝突の解決策として考えられた。レコードの格納領域は、ハッシュ値ごとのブロックに分けられ(索引部)、ブロック内でレコードは順編成される。ブロックの探索:直接探索
ブロック内の探索、追加、削除:順編成の探索、追加、削除
以下のデモでは簡単のため、5で割った余りをハッシュ値にしている。
| 探索、追加、削除にかかる(平均あるいは最悪の)ステップ数を示し、理由を説明せよ。 |
第7節 2分探索木
2分探索木は、2分探索と探索後に定数ステップでの追加・削除が可能な木構造である。各節点は左子と右子を(該当レコードがあれば)持ち、次の条件を満たす
左子の値<節点の値<右子の値
探索:木の根(最上節点)から始めて、次を繰り返す
見つかれば、終了
節点の値より小⇒左部分木を探す
節点の値より大⇒右部分木を探す
追加:探索で場所を見つけそこに追加する
削除:削除節点 n を探索。n の子が
1子以下なら、子を n の位置に移動する
2子なら
左部分木中の最大値節点を削除し
その最大値を n に代入する
| 探索、追加、削除にかかる平均のステップ数を示し、理由を説明せよ。 |
注.このアプリでは、これまでの例と異なり、データの重複を禁止している。