コンピュータの基礎第２講
情報とデータ
【第２講のポイント】
この章では、情報とは何かについて考え、それがどのようにコンピュータで処理可能な形に表現されるかについて学ぶ。(参考：川合慧著「情報」東大出版会)
【第２講の目標】学習後、以下のことが身についたかチェックしよう。
- 「情報」、「データ」、「符号」という術語の意味がわかる
- 「情報量」の定義が分かり、ビットが情報量の単位であることを理解する
- モデルが、「完全」、「一意」、「忠実」、「整合」、「冗長」であることの意味が言える
- 以下の情報モデルを理解する
- ネットワークモデル
- 階層モデル
- 関係モデル
- 集合・論理モデル
【第２講の構成】
- 情報・データ・符号
- 情報量とビット
- 情報のモデル化
- モデルのタイプ
1
第１節 情報・データ・符号
情報とデータ
「情報」と「データ」とは、区別にあいまいなところがあり、意味が必ずしも一定していないが、ここでは次のように定めておこう。- 情報
- 「事物・出来事などの内容・様子。また，その知らせ。」(大辞林)とあるように、何らかの伝えるべき内容を包含するもの。
- データ
- 情報の表現であって、伝達、解釈または処理に適するように形式化され、再度情報として解釈できるもの（情報処理用語・基本用語）であり、音や絵、長さ、重さ、時間のような連続値を持つアナログデータと文字や整数のような離散的な値のデジタルデータがある。
この定義では、情報はそれ自身必ずしも形を持たない抽象的な「概念」であり、「データ」として表現されて、初めて形を持ち処理・伝達される。データを(それが表す）の解釈が可能になるためには、データが存在する文脈、すなわち、データ表現に関する規約が必要である。
例えば、一方が日本語を話しているつもりで、他方が英語を聞いているつもりでいれば、当然意味は通じない(情報は伝達されない)。それほど極端な例でなくても、伝言ゲームのように、データが送り手と受け手で異なった情報として解釈されることは、むしろ普通のことである。以下の図は「四角」というデータによって情報が(誤)伝達される様子を図示している。
| 情報： □ | 情報伝達 | 情報： ■ |
| 表現↓ |
解釈↑ |
|
| データ： 四角 |
伝達 ――→ |
データ： 四角 |
符号
さらに、この授業では、データをコンピュータで処理するために 0,1 の列で表現したものを符号と呼ぶ。2
アナログとデジタル
データには、アナログデータとデジタルデータがある。アナログデータは、連続的に変化する情報(データ)を、連続的な形式で表現(記録)したデータである。例えばフィルム写真や絵画、テープに記録された音声、時間を表す時計の針(の位置)、水銀体温計の水銀柱の長さ等はアナログデータである。デジタルデータは、数字や文字・記号によって(離散的に)表現されたデータをいう。（岡本先生のパワーポイント）
アナログデータをデジタルデータに変換する操作をAD変換という。例えば、重さ、長さ、温度などを測定し目盛を読んで数値化することや、デジタルカメラで写真をとることはAD変換である。一方、AD変換によって得られたデジタルデータから元のアナログデータを復元する操作をDA変換という。
デジタルデータやアナログデータの特徴をまとめておこう。
アナログデータ
- デジタル化の際に生じる誤差がない
- 複製・通信・再生の際に雑音の影響を受け劣化する
- データ処理には、処理ごとに異なる機器や電気回路が必要
レンズ(フィルター)、イコライザー、など
- デジタル化の際に誤差が生じる
- 複製・通信が容易で情報が失われない ⇒ コピー・著作権の問題が生じる
- データ処理はプログラム(コンピュータ)で自由にできる
- データを圧縮できる
アナログデータのままデジタル化せずに処理する簡単な例として
|
|
3
情報処理
コンピュータの発達に伴い、コンピュータによる情報(データ)処理が様々な場面で使われるようになった。コンピュータは 0,1 で動くので、コンピュータで処理するためには、情報を最終的には 0,1 で表現しなければならない。情報がデジタルデータで表現されれば、それを 0,1 で符号化すればよいが、アナログデータで表現されている場合、アナログデータをデジタルデータに変換(AD変換)してから 符号化しなければならない。データをコンピュータ内部でどのように符号化(表現)するかについては、後で詳しく解説する。
| 情報 | 表現→ ←解釈 |
(アナログ データ) |
(AD変換→) (←DA変換) |
デジタル データ |
表現→ ←解釈 |
符号 (0,1) |
以下は、データ処理の簡単な例として白黒の絵(アナログデータ)を、コンピュータで(白と黒を)反転する過程を模式的に表したものである。
- Aという文字が書かれた(白黒の)絵を、スキャナーで取り込み、画素(格子のマス)ごとの白黒データに変換する(AD変換)
- スキャナーが白を0、黒を1で表したデータ(符号)を作る(符号化)
- コンピュータが符号中の0を1に、1を0に置き換える(データ処理)
- プリンタが0を白、黒を1に解釈して、印刷する(DA変換)
| スキャナ | コンピュータ | プリンタ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A (絵) |
AD変換 ―→ |
|
符号化 ―→ |
|
データ処理 ―→ (0,1反転) |
|
解釈 ―→ |
|
DA変換 ―→ (印刷) |
A (絵) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
結局のところ、コンピュータ本体が行うデータ(情報)処理は、0,1の列(符号)から別の0,1の列(符号)を得ることに他ならない。
4
第２節 情報量とビット
情報には大事な(価値のある)情報もあればそうでないものもある。一方、同じ情報でもそれを表すデータの量は、表し方で異なる。では、情報それ自体の量はどうすれば定義できるだろうか。直感的には、めったにないこと「宝くじの一等に当たった」「交通事故にあった」等の情報量は大きく、よくあること「雨に降られた」等の情報量は小さいだろう。シャノンは情報の大きさ(価値)を表す情報量を次の条件から定義した。
- 情報量f(p)はその情報が知らせる事柄の生起確率 p から定まる
- 確率 p が小さいほど情報量f(p)は大きい
- 独立に生起する２つの事柄をともに知らせる情報量は、各々の情報量の和になる
- 最少の情報は、等確率でおこる2つの値(ON/OFF、真/偽、左/右、0/1、等々)のどちらかであるという情報で、その情報量を f(1/2)=1 (ビット)とする
|
| コラム．対数関数 |
| 指数法則 ay×ay'＝ay+y' では、aのべき乗の積がaの指数の和になる。aのべき乗x=ayに対しaの指数yを出力する関数を y=loga(x) と表し(底aの)対数関数という。即ち y=loga(x)⇔x=ay で、loga(xx')=loga(x)+loga(x') が成立つ。よって f(p)=loga(p) は条件3を満たす。さらに log2(1/2)=-1 なので、f(p)=-log2(p) とすれば条件4や2も満たす。 また、対数の表があると積が和で求まる。この原理を利用したのが計算尺である（シミュレータ）。 |
5
第３節 情報のモデル化
対象のモデル化
われはわれは抽象的な対象であれ、具体的な対象であれ、対象をそのまままるごと認識できるわけではない。何らかのモデルを援用して対象を認識し、情報を抽出し、データとして表現・理解(し、さらにはコンピュータ処理のために0，1で符号化)する。ここではその過程を３つのレベルに分けて整理しておこう。- 概念モデル
対象を認識する際に援用するモデル。言い換えると、人は(意識するしないに関わらず)何らかの概念モデルを用いて、対象の特定の側面を抽出し、概念を形成する。情報はこのレベルに対応すると考えられる。 - 論理モデル
対象(の概念モデル)を言葉や文字、記号で表現する際のモデル。対象の論理的構造や対象間の関係が記号的に表現され、処理や操作が可能になる。通常、われわれは、このレベルのデータ(情報)を処理・操作し、互いに交換している。 - 物理モデル
物理的な表現レベルのモデル。例えば、コンピュータ内部でのデータ表現(符号)がこれにあたり、機械的な操作を問題にする際に援用する。
6
モデル化の性質
一般にモデルを構築し操作する際、元となる対象(世界)との次の様な関連が問題となる。- 完全性
- 対象とする世界の全要素に対して、モデル内に対応する表現がある時、モデルは完全であるという。例えば、「さいころの目」のように要素が有限個ならば、1～6までの自然数で完全に表現できるが、アナログ(連続値)データをデジタル(離散値)データで表現する(AD変換)場合に、完全なモデルを作ることは困難であり、DA変換で戻しても、元のアナログデータの近似値にしかならない。
- 一意性
- モデルの表現が表す要素(解釈)が一つに定まるモデルは一意的であるといい、そうでないモデルはあいまいであるという。例えば、各個人をその氏名で表すモデルは、同姓同名の人がいた場合にあいまいになる。その場合、住所を付加して一意なモデルが作るようなことが行われる。
- 忠実性
- 一意性の逆で、対象の１要素に対して、モデルの１表現が対応する場合、そのモデルは忠実であるという。忠実でないモデルでは、対象のある要素が複数の表現を持ち、モデル内の操作は(どちらの表現を操作するか不明なため)複雑になる。したがって、忠実でないモデルにおいては、表現の標準化を行って、忠実なモデルに変換することが行われる。例えば、有理数に対する分数表現は1/2=2/4=3/6=・・・のように忠実でないが、分母が正の既約分数に限れば(標準化すれば)、忠実なモデルとなる。
- 整合性
- モデルが表現する世界では通常、各要素が孤立して存在するのではなく、要素間の何らかの関係や操作(演算)が定義され、その関係や操作が満たす規則(性質)が存在する。このような関係や操作はモデルの世界にも移行されることになるが、その際、対象の世界で成り立つ規則(性質)がモデルの世界でも成り立つとき、モデルは整合的であるという。例えば、実数の世界では(1/3)×3＝1であるが、それを小数点以下４桁までで表現した(あいまいな)モデルでは(1/3)×3＝0.3333×3＝0.9999≠1となり、整合的ではない。
7
- 冗長性
- 本質的に同じ情報(データ)が表現中の複数箇所に現れたり、本質的でない表現が含まれるモデル(表現)は冗長であるという。通常われわれが用いる表現(言語、絵画、音楽等)は冗長であり、それゆえその一部が欠落したとしても、情報が正しく伝達されることが多い。それに対して冗長でない表現は、短く効率的ではあるが、一部でも欠落すると情報が正しく伝わらない。例えば、答案用紙で解答者を学籍番号と氏名で表現するのは、誤りを防ぐ、あるいは誤りがあっても情報が正しく伝わるように、冗長性を利用している。
| 実数は原理的に無限の桁数を持つから、各々の実数にその表現を作成することはできない。したがって実数の論理モデルは一般的に【 】である。 有理数の分数表示は【 】でない(-1/2=2/(-4)=…)ので、(分母が正の)既約分数表示に標準化することによって、【 】なモデルが構成される。 通常コンピュータでは実数を有限桁数で表現している。仮に、(何桁でも同様だが)小数点以下4桁で四捨五入するとしよう。その場合、0.3325以上0.3335未満の数はすべて0.333と表現されるので【 】ではない。また、実数の世界では成り立つ規則1/3×3=1が、モデル(表現)の世界では成り立たず(1/3×3=0.333×3=0.999≠1)【 】ではない。 |
このように、コンピュータで処理されるデータモデルは、もとの対象（情報）を正しく表現しているとは限らないので、注意が必要である。
8
第４節 モデルのタイプ
対象の論理モデルを構築する際には、対象に対する深い理解のもとに適切な表現（モデル）を選択する必要がある。ここでは、よく用いられるモデルの代表的なタイプを紹介する。グラフモデル
対象を○や□で、対象の間の関係を実線や矢印で、図式的に表現したモデルをグラフモデル、あるいはネットワークモデルという。例えば路線図や会社の組織図など、グラフモデルは、実生活の様々な場面で使われている。インターネット上のWebページとその間のリンクや、ゲームの局面と(指し手による)その間の移動なども、グラフでモデル化できる。
例．東京メトロ路線図、ウォルトディズニーの戦略図(日経BP社)
例．東京メトロ路線図、ウォルトディズニーの戦略図(日経BP社)
| Stanley Milgram は、アメリカの人間を対象にした友人ネットワークグラフで、人間の間の距離(到達に要する実線の数の最小値)の最大値がそれほど大きくないことを発見し、スモールワールド現象と呼んだ。その値はいくつか。言い換えると、友達の友達の友達の・・・というように、友達関係を最少何人たどればアメリカ人同士が友達になれるか。 |
階層モデル
対象の分類(クラス分け)とその間の包含・所属関係を表現したグラフモデルを階層モデルという。分類図、住所、組織図等、実生活でもよく使われる。通常、根元(出発点)となる一つの要素から次々に枝分かれしていくことから、木構造とも呼ばれる。また、階層モデルは、出発点を持ち、矢印や実線の列が閉じて(交わって)いないグラフモデルでもある。例えば、局面が循環することのないゲームは初期局面を出発点とする木構造でモデル化できる(ゲーム木)。コンピュータのファイルシステムは、ドライブ(記憶装置)を出発点とする階層モデルである(エクスプローラを起動し、表示→ナビゲーションウィンドウを表示させてみよ)。さらに、条件判断を重ねて行われる意思決定の全体をモデル化した木構造は、決定木と呼ばれる。また、右図はヘッケルの系統樹 (Wikipedia)である。
9
| グラフモデルと階層モデルの違いを述べよ。 |
関係モデル
例えば、(学籍番号、名前、住所、連絡先)などのように、いくつかの項目の値の組みの集まりを関係(表)という。情報をいくつかの関係(表)の集まりで表現するモデルを関係モデルという。関係モデルについては、データベースの章で詳しく議論する。
例．
学生の表
成績の表
例．
学生の表
| 学籍番号 | 名前 | 住所 | 連絡先 |
| 1234567a | 田中 花子 | 東京都多摩市唐木田１－２ | 090-5555-1111 |
| 2341156c | 山口 花子 | 東京都立川市１２３－４５ | 042-567-4321 |
| ・・・ | ・・・ | ・・・ | ・・・ |
成績の表
| 科目名 | 教員名 | 年度 | 学期 | 学籍番号 | 点数 |
| コンピュータの基礎 | 山崎 秀記 | 2010 | 夏 | 1234567a | 90 |
| 英語 | 大妻 タカ | 2009 | 冬 | 2341156c | 75 |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
|
10
集合(論理)モデル
対象が何らかの要素の集まりからなるとき、それを集合と捉えるのが一般的である。例えば 素数(の集合)＝{x|xの約数はxと1のみ}というように、集合はそれを規定する条件と同一視できることから、論理モデルと考えることもできる。集合(論理)モデルは、基礎的なモデルとして、他のモデルと組み合わせて使われることも多い。
集合間の操作としては、積(∩ 共通部分)、和(∪)、否定(~ 全体集合との差)があり、それぞれ論理演算子の、かつ(∧ 論理積)、または(∨ 論理和)、否定(￢)に対応する。また、これらの集合操作(論理演算子)の組み合わせですべての集合(論理)演算が定義できることが知られている。
例．論理式検索では、複数のキーワードに対して、それ(を含むという条件)の かつ(単に並べる)、または(OR)、否定(-)、の組み合わせで検索条件を指定できる。
集合間の操作としては、積(∩ 共通部分)、和(∪)、否定(~ 全体集合との差)があり、それぞれ論理演算子の、かつ(∧ 論理積)、または(∨ 論理和)、否定(￢)に対応する。また、これらの集合操作(論理演算子)の組み合わせですべての集合(論理)演算が定義できることが知られている。
例．論理式検索では、複数のキーワードに対して、それ(を含むという条件)の かつ(単に並べる)、または(OR)、否定(-)、の組み合わせで検索条件を指定できる。
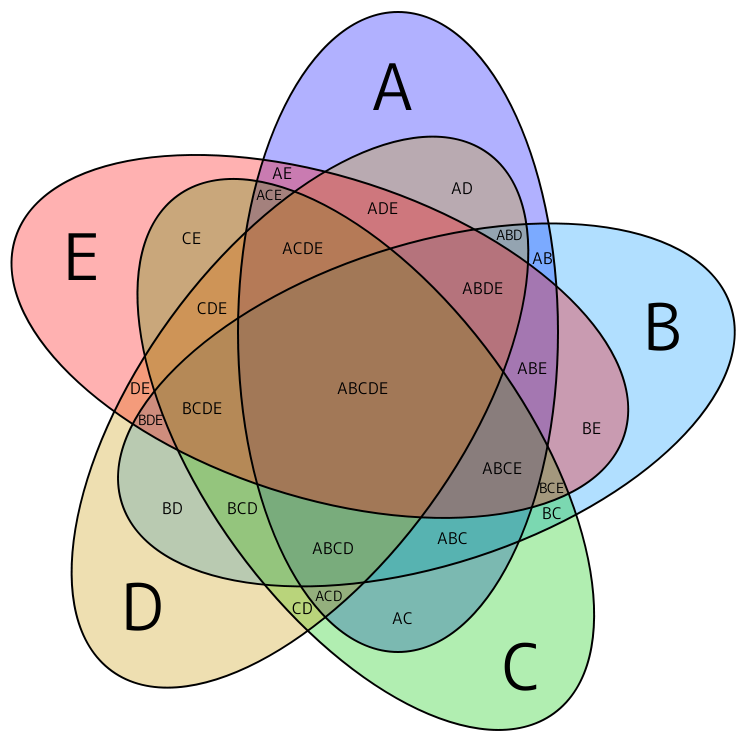いくつかの集合の関係を図示したものをベン図という。５集合までは、ベン図を２次元平面上に何とか描くことができる（右図）が、６個以上では簡明に描くことは難しい。しかし、集合(条件)がいくつであっても、次の問いの議論から、それらの組み合わせで表される集合(条件)はすべて、もとの集合(条件)から∩、∪、~(∧、∨、￢)演算の組み合わせで表現できる。これを∩、∪、~ (∧、∨、￢)の完全性という。11
１．右図は、集合A、B、C のベン図である。0 から 7 までの番号を付けた集合(条件)を表す集合演算式(論理式)を下表の空欄に記述せよ。また、A の欄には、対応する集合が A に含まれない場合は 0 を A に含まれる場合は 1 を入れ、B、C の欄にも同様に記入せよ。
２．集合(条件)A、B、Cで区分けされる集合(条件)はすべて、0から7までの番号づけられた集合(条件)の和集合(論理和)で表されるから、A、B、Cから∩、∪、~(∧、∨、￢)の組み合わせで表される。 １)１と３と５の和集合(論理和)を表す集合演算式(および論理式)を求めよ。 ２)１と３と５の和集合(論理和)を表す集合演算式(および論理式)をできるだけ簡単な形で表せ。 ３．5集合ベン図では、全体集合がいくつの集合(領域)に分割されているか。 |
12
Previous
Next