第７講　CPUの仕組みと演算回路　 1講 2講 3講 4講 5講 6講　 8講 9講 10講 11講 12講 13講 14講

コンピュータの基礎第７講
CPUの仕組みと演算回路


【第７講のポイント】
本講では、CPUの構成と動作の仕組みについて学ぶとともに、コンピュータを直接動かすアセンブリ命令がどのようなものかについて学ぶ。さらに、CPUの演算回路の設計原理について学び、コンピュータがどんどん小さくなっている秘密についても原理的に理解する。

【第７講の目標】
学習後、以下のことが身についたかチェックしよう。
  1. 次の言葉の意味がわかる
    命令カウンタ、命令レジスタ、汎用レジスタ
  2. クロック周波数とflopsの違いを理解する
  3. CPUの基本動作サイクルを理解している
  4. CPUが実行する基本的な命令の種類が分かる
  5. アセンブリプログラムの基本を理解する
  6. 演算回路の設計原理を理解している
  7. 演算回路が基本論理素子(AND、OR、NOT)から構成できることがわかる
  8. 演算回路が１種類のスイッチ素子から構成できることがわかる
  9. コンピュータの基本部品が、歴史的にリレー、真空管、トランジスタ、集積回路と変化してきたことを理解している
  10. 集積回路について理解している

【第７講の構成】
  1. CPUの基本動作
  2. CPUの命令の種類
  3. アセンブリ言語超入門
  4. 演算(論理)回路
  5. 加算器(回路)の設計
  6. 集積回路

第１節　CPUの基本動作

CPU 　CPU(Central Processing Unit、中央演算処理装置)は、コンピュータの頭脳部で計算や制御をつかさどる。CPUは、クロック、命令カウンタ、命令レジスタ、命令デコーダ、（複数の）汎用レジスタ、演算回路等の部品から構成される。各部品はクロックに同期して(タイミングを合わせて)動作するが、その頻度をクロック周波数という。２GHｚ(ギガヘルツ)であれば毎秒2ギガ(20億)回動作する。
　同種のCPUであればクロック周波数が大きいほど処理速度が速くなるが、異種のCPUの比較では大きい方が速いとは限らない。
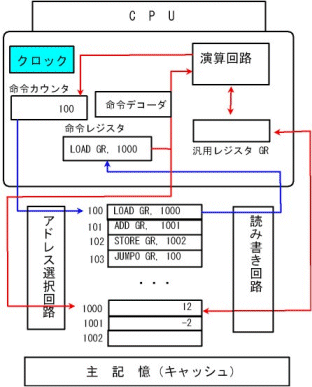CPUの動作の図 　コンピュータ(CPU)はメモリーに貯えたプログラム(命令の列)を逐次実行する。CPUの基本動作サイクルを簡単に説明すると以下のようになる。
  1. 命令カウンタ中の番地をアドレス選択回路に送る。
  2. アドレス選択回路が選んだ番地の内容(命令)を、読み書き回路が命令レジスタに送る。
  3. 命令カウンタの値が1(命令が占める領域分)増やされる。
  4. 命令デコーダが命令を解読する。
  5. 演算回路、汎用レジスタ等を用いて、解釈された命令が実行される。
　最初にこの方式のコンピュータの設計にたずさわったノイマン(Von Neumann)に因んで、プログラム内蔵方式(ノイマン型コンピュータ)と呼ばれ、現在までその基本原理は変わっていない。

*問７．１．CPU内の次の部品の役割・機能を説明せよ。 （ヒント）
　1．クロック　　　2．命令カウンタ　　3．命令レジスタ　　
　4．命令デコーダ　5．汎用レジスタ　　6．演算回路
　CPUの能力を、flops(FLoating-point Operations Per Second)という1秒あたりの浮動小数点(実数)演算回数で計ることもある。手元のパソコンのflops値を計測するにはIntel®MKLベンチマークパッケージ中のLINPACKベンチマークを利用するとよい。日本語で、Windows対応ソフトのダウンロード⇒実行やMac対応ソフトのダウンロード⇒実行の手順説明がある。
　また、CPUが一度に処理するビットサイズ(2進桁数)によって、32ビットマシーン、64ビットマシーンなどという。

問７．２． （ヒント）
  1. クロック周波数とflopsの違いを説明せよ
  2. 自分のパソコンのflops数を調べよ
  3. 自分のパソコンが何ビットマシーン(のOS)かを調べよ
    　　（ヒント：コンピュータのプロパティを見るとよい）

コラム．　マルチコア(cores)、マルチスレッド(threads)
私のノートパソコンのflops測定結果をこちらに示す。終了前に止めたが、クロック周波数(CPU frequency)2.6GHzに対し平均82G(ギガ)Flopsでている。実は最近のCPUは前ページで説明したCPU(演算ユニット、コア)を複数備えており、複数の処理(スレッド)を並行させたり、1クロックの間に複数の浮動小数点演算を行うなど様々な工夫が可能な場合のflopsを測っている。
　因みに、姫野ベンチマーク(Macでの実行は難しい)では、2.16GFlopsと、これらの工夫が除かれた数値が得られる。

コラム．　コンピュータの遂次性と局所性
コンピュータは高速大容量である。しかし、大量データを一瞬のうちに処理でき(るように見え)てもそれらを同時並列的に処理できるわけではない。CPUは、64(32)ビットの極めて小さなデータに対する単純な命令を逐次的に実行する。そのデータサイズは画像なら1,2点の色情報に過ぎない。
　人は、画像全体を眺めて｢空の絵｣や｢青っぽい｣等と判断する。コンピュータが｢青っぽい｣と判断するには、画像の点を一つ一つ調べ、青い点が何パーセント以上含まれる、といった計算が必要になるだろう。一般に、与えられた画像が何の絵かを正確に判断すること（画像認識）はコンピュータにとって容易ではなく、ＡＩ（人工知能）の主要テーマでもある。
　コンピュータ処理の局所性は、キャッシュがうまく働く理由にもなっている。人が大きな画像全体を眺めるときのように、メモリー全体に散らばっているデータをランダムに読み書きするとキャッシュ中のデータの置き換えが頻繁に生じて効率は著しく低下するが、通常そのようなことは起きない。
　コンピュータ処理のこのような逐次性と局所性を理解することは、コンピュータと付き合う上で重要なポイントである。これについては梅津信幸著「あなたはコンピュータを理解していますか」(技術評論社) を薦める。

第２節　CPUの命令の種類

CPUが実行する基本的な命令には以下のようなものがある。
  1. 取り出し(LOAD)命令
    LD GR,2000（2000番地の内容を汎用レジスタGRに取り出せ）なら、
    番地(2000)をアドレス選択回路に送り、読み書き回路を通して、その内容を汎用レジスタに入れる。
  2. 格納(STORE)命令
    ST GR,2002（汎用レジスタGRの内容を2002番地に格納せよ）なら、
    番地(2002)をアドレス選択回路に送り、読み書き回路を通して、汎用レジスタの内容をメモリーに格納する。
  3. 演算命令、比較命令
    ADD GR,2001（2001番地の内容を汎用レジスタGRに加えよ）なら、
    番地(2001)をアドレス選択回路に送り、読み書き回路を通してその内容を取り出し、演算回路を使って汎用レジスタに加える。
  4. 分岐命令：次に実行する命令(の番地)を指定する
    JPL GR,1001（GRの内容が正なら1001番地に飛べ）なら、
    汎用レジスタの値が正の値なら番地(1001)を命令カウンタに入れる。
  5. 入出力命令：IN, OUTなど
  6. その他：START, ENDなど
などがある。他にも種々あるが、詳しくはCASLII(情報処理技術者試験で使用されるアセンブリ言語)をCASLII入門講座で調べてみよ。

機械語とアセンブリ言語

コンピュータは 0，1で動くので、実は上のような（文字等で表された）命令を直接実行できるわけではない。CPUが直接理解(実行)できる形の命令(0,1の列)を機械語といい、それを上のような形で(人間に分かりやすいように)文字や記号で表現したものをアセンブリ言語という。機械語の命令とアセンブリ言語の命令は原則１対１に対応し、アセンブリ言語を機械語に翻訳するプログラムをアセンブラという。

第３節　アセンブリ言語超入門

　本節では、アセンブリ言語がどんなものか体験的に理解するために、簡単なアセンブリプログラムを読み解いてみよう。

番地内容
1000LD GR 2000
1001ADD GR 2001
1002ST GR 2002
…・・・
2000500
200150
2002
…
　メモリ内に左表のようにアセンブリ命令とデータ(実際は機械語と2進データ)が格納されていて、命令カウンタの値が1000のときの、コンピュータ(CPU)の動作を考えてみよう。
　計算過程における命令カウンタ、命令、汎用レジスタ、メモリの値の変化は下表のようになる。（10進表示しているが本来は2進表示）
カウンタ　命令　 GR 200020012002備考
11000LD GR 200050050050
21001ADD GR 200155050050550=500+50
31002ST GR 200255050050550

　これらの例題や次ページの問からもわかるように、アセンブリ言語によるプログラム(プログラミング)も人間にとって必ずしも分かりやすいものではない。そこで、より分かりやすい表現を目指して、高級言語が開発された。詳しくは後述するが、最初の高級言語FORTRANは FORmula TRANslation の略で、プログラム中に数式が書けるようにしていた。
CPUの実行サイクルは、計算過程の表で説明すると、以下の手順を繰返す。
  1. (命令)カウンタ中の番地にある命令を命令欄(レジスタ)に送る
  2. 次のサイクル用に、(命令)カウンタの値を1増やして次行に記入する
  3. 命令にしたがって、GRや各メモリー番地、JPL等のジャンプ命令では次行のカウンタ、の内容を更新する

*問７．３． （ヒント）
　メモリ内に左図のプログラムとデータがあり、命令カウンタの値が1000であるとする。
1. 上記説明や前ページの例にならって、コンピュータ(CPU)の計算過程を示し、END(終了)命令に到達したときの2002番地の値を求めよ。ただし新たな命令の意味は以下の通りであるとする。
　SUB GR 2001 はGRから2001番地の値を引く命令
　JPL GR 1001 はGRの値が正ならば命令カウンタの値を1001にする命令
番地内容
1000LD GR 2000
1001SUB GR 2001
1002JPL GR 1001
1003ADD GR 2001
1004ST GR 2002
1005END
…・・・
20008
20013
2002
…
カウンタ　　　命令　　　 GR 200020012002
1100083
2
3
4
5
6
7
8
9
10
11

2. 2000番地の値が 35で 2001番地の値が 4のとき、END命令に到達したときの 2002番地の値はいくつか。

第４節　演算(論理)回路

　CPUでの演算は、加算でも他の演算でも、結局のところ与えられた複数の32ビット入力列から32ビット出力列を求めることに他ならない。ここでは、CPUの演算回路が AND, OR, NOT という3種類の論理素子からすべて構成できることをみてゆこう(第２講の集合・論理モデルの項を参照)。
X￢X
01
10
X YX∧YX∨Y
0 000
0 101
1 001
1 111

AND、OR、NOT 素子とその真理値表

　∧(AND)、∨(OR)、￢(NOT) の素子は右の真理値表を持つ。ここで 0⇔偽、1⇔真と対応させたとき、それぞれ、￢(NOT)は真偽を反転、∧(AND)は入力がともに1(真)のときのみ1(真)、∨(OR)は入力のどちらかが1(真)のときに真、という働きをもつ。

実習．Kazuhiko Arase 氏による論理回路シミュレータSimcirJS
{"width":320, "height":250, "showToolbox":true, "toolbox":[ {"type":"NOT"},{"type":"AND"},{"type":"OR"}, {"type":"DC"},{"type":"LED"},{"type":"Toggle","label":"x"},{"type":"Toggle","label":"y"} ], "devices":[ {"type":"DC","id":"dev0","x":8,"y":16,"label":"DC"}, {"type":"LED","id":"dev1","x":160,"y":16,"label":"LED"}, {"type":"Toggle","label":"X","id":"dev2","x":56,"y":16,"state":{"on":false}}, {"type":"DC","id":"dev3","x":8,"y":80,"label":"DC"}, {"type":"Toggle","label":"X","id":"dev4","x":56,"y":80,"state":{"on":false}}, {"type":"LED","id":"dev5","x":160,"y":80,"label":"LED"}, {"type":"NOT","id":"dev6","x":112,"y":80,"label":"NOT"}, {"type":"Toggle","label":"X","id":"dev7","x":56,"y":136,"state":{"on":false}}, {"type":"Toggle","label":"Y","id":"dev8","x":56,"y":192,"state":{"on":false}}, {"type":"AND","id":"dev9","x":120,"y":160,"label":"AND"}, {"type":"LED","id":"dev10","x":168,"y":160,"label":"LED"}, {"type":"DC","id":"dev11","x":8,"y":160,"label":"DC"} ], "connectors":[ {"from":"dev1.in0","to":"dev2.out0"}, {"from":"dev2.in0","to":"dev0.out0"}, {"from":"dev4.in0","to":"dev3.out0"}, {"from":"dev5.in0","to":"dev6.out0"}, {"from":"dev6.in0","to":"dev4.out0"}, {"from":"dev7.in0","to":"dev11.out0"}, {"from":"dev8.in0","to":"dev11.out0"}, {"from":"dev9.in0","to":"dev7.out0"}, {"from":"dev9.in1","to":"dev8.out0"}, {"from":"dev10.in0","to":"dev9.out0"} ] }
右のシミュレータでは、電源(DC)につながった入力ボタン(X,Y)をクリックすると、そのON(1)/OFF(0)に応じて回路の出力LEDが点(1)滅(0)する。
① NOT素子とAND素子の働きを調べよう。
② AND素子をOR素子に置き換えてその働きを調べよう

双対な論理式

X￢X
10
01
X YX∨YX∧Y
1 111
1 010
0 110
0 000
　∧と∨の真理値表において、変数X,Yの値も含めて0と1を交換すると、∧が∨になり∨が∧になる。さらに、￢の真理値表は0と1を交換しても変わらない。（右の表）
　そこで、∧、∨、￢から構成される論理式に対して、0と1、∧と∨を交換した論理式を双対論理式と呼ぶ。双対論理式という概念は双対的で、双対論理式の双対論理式はもとの論理式と一致する。
論理式の等式⇔双対論理式の等式
X∧￢X＝0⇔X∨￢X＝１
X∨(X∧Y)＝X⇔X∧(X∨Y)＝X
　2つの論理式が等しければ、それらの双対論理式同士も等しい。これを論理式の双対性という。

第５節　加算器（回路）の設計

演算回路で行われる様々な演算を実現する原理を見てゆこう。本節では、加算回路の設計を例に説明するが、他の演算でも同様である。
A BA+Bの
上の桁C		A+Bの
下の桁S
0 000
0 101
1 001
1 110

半加算器の論理式と回路

　1ビットの加算を行なう半加算器（回路）を考えよう。加算の結果は、桁上がりを含めた上下の桁を表にすると右表になる。上の桁はANDそのものであるが、下の桁はどのような回路を組めばよいだろうか。
　与えられた真理値表を持つ論理式あるいは回路を作る手順を考えよう。ここでは、入出力ともに1ビットで2変数の場合を考えているが、ビット数や変数が増えても同様である。
  1. 真理値表で値が1の行に対し、その行でだけ1で他はすべて0である真理値表を持つ論理式を求める。そのために、A=0を意味(真偽が一致)する論理式が￢Aであり、A=1を意味する論理式がAであることに注目しよう。したがって、求める論理式を得るには、値が1である行において、入力値が0の変数には￢(NOT)を付けた上で、すべての変数を∧(AND)で結ぶ。
  2. 与えられた真理値表を持つ論理式を得るには、値が1である行において上で求めた論理式を、∨(OR)で結ぶ。
その結果得られる論理式を下表に記述している。確認してみよう。
A BA+Bの
上の桁C		A+Bの
下の桁S		その行でだけ1
になる論理式
0 000￢A∧￢B
0 101￢A∧B
1 001A∧￢B
1 110A∧B
論理式C=A∧BS=(￢A∧B)∨(A∧￢B)
実験．論理式の真理値表
　右の欄に論理式を入力して[評価]を押すと真理値表が表示される。論理記号は &(∧), |(∨), !(￢) を用い、例えば (￢x∧y)∨(x∧￢y) は !x&y|x&!y と表せる。
　以下の論理式を入力して、上の議論を確かめてみよ。
  1. !x&y
  2. x&!y
  3. !x&y|x&!y

前ページで求めた論理式から、回路を構成すると下のようになる。A, B のボタンを ON/OFF して、C S に A+B が求まることを確認しよう。
{ "width":450, "height":200, "showToolbox":true, "toolbox":[ {"type":"NOT"}, {"type":"AND"}, {"type":"OR"}, {"type":"DC"}, {"type":"LED"}, {"type":"Toggle"} ], "devices":[ {"type":"DC","id":"dev0","x":8,"y":48,"label":"DC"}, {"type":"NOT","id":"dev1","x":136,"y":8,"label":"NOT"}, {"type":"AND","id":"dev2","x":144,"y":136,"label":"AND"}, {"type":"AND","id":"dev3","x":192,"y":16,"label":"AND"}, {"type":"Toggle","id":"dev4","x":64,"y":8,"label":"A","state":{"on":false}}, {"type":"AND","id":"dev5","x":192,"y":72,"label":"AND"}, {"type":"NOT","id":"dev6","x":136,"y":80,"label":"NOT"}, {"type":"Toggle","id":"dev7","x":64,"y":80,"label":"B","state":{"on":false}}, {"type":"LED","id":"dev8","x":248,"y":136,"label":"C"}, {"type":"OR","id":"dev9","x":240,"y":40,"label":"OR"}, {"type":"LED","id":"dev10","x":296,"y":136,"label":"S"} ], "connectors":[ {"from":"dev1.in0","to":"dev4.out0"}, {"from":"dev2.in0","to":"dev4.out0"}, {"from":"dev2.in1","to":"dev7.out0"}, {"from":"dev3.in0","to":"dev1.out0"}, {"from":"dev3.in1","to":"dev7.out0"}, {"from":"dev4.in0","to":"dev0.out0"}, {"from":"dev5.in0","to":"dev4.out0"}, {"from":"dev5.in1","to":"dev6.out0"}, {"from":"dev6.in0","to":"dev7.out0"}, {"from":"dev7.in0","to":"dev0.out0"}, {"from":"dev8.in0","to":"dev2.out0"}, {"from":"dev9.in0","to":"dev3.out0"}, {"from":"dev9.in1","to":"dev5.out0"}, {"from":"dev10.in0","to":"dev9.out0"} ] }

　このように、コンピュータの演算回路はAND(∧)、OR(∨)、NOT(￢)の素子があれば組み立てられることがわかる。

全加算論理式

複数桁の加算では、桁上がりを含めた３変数の加算（全加算という）を考慮する必要がある。全加算を実現する論理式がわかれば、それから（原理的には）全加算器（回路）を構成することができる。

*問７．４．全加算器を実現する論理式 （ヒント）
A B CinA+B+Cinの
上の桁Cout		A+B+Cinの
下の桁S		その行だけ
1の論理式
0 0 000
0 0 101￢A∧￢B∧Cin
0 1 00￢A∧B∧￢Cin
0 1 110￢A∧B∧Cin
1 0 001A∧￢B∧￢Cin
1 0 110A∧￢B∧Cin
1 1 01
1 1 11A∧B∧Cin
論理式Cout=
S=
　右表は桁上がりCの項も含めた全加算器の真理値表である。
  1. 空欄を埋めよ
  2. 上の桁Coutを表す論理式を求めよ
  3. 下の桁Sを表す論理式を求めよ
ヒント：第２講の集合(論理)モデルを参考にせよ

この真理値表から、直接論理回路を構成することができるが、実際には、次に説明するような手法で段階的に構成される。

加算回路

　半加算器(１桁目)と全加算器(残りの桁)をつなげれば、加算回路が実現できる。

*問７．５．以下の問で加算器を HA1, FA1 等と略記し、つなぎ方を Cin→HA2のA のように記述せよ （ヒント）
  1. 半加算器2器とOR素子を使って全加算器を構成するつなぎ方を記述せよ
  2. 半加算器1器と全加算器3器を使って、2進4桁の加算器（回路）を構成するつなぎ方を記述せよ

{ "width":450, "height":460, "showToolbox":true, "toolbox":[ {"type":"HalfAdder"}, {"type":"FullAdder"}, {"type":"OR"}, {"type":"NOT"}, {"type":"AND"}, {"type":"DC"}, {"type":"LED"}, {"type":"Toggle"}, {"type":"4bitAdder"} ], "devices":[ {"type":"DC","id":"dev0","x":0,"y":64,"label":"DC"}, {"type":"Toggle","id":"dev1","x":56,"y":192,"label":"A0","state":{"on":false}}, {"type":"Toggle","id":"dev2","x":56,"y":248,"label":"A1","state":{"on":false}}, {"type":"Toggle","id":"dev3","x":56,"y":352,"label":"A3","state":{"on":false}}, {"type":"Toggle","id":"dev4","x":56,"y":304,"label":"A2","state":{"on":false}}, {"type":"Toggle","id":"dev5","x":112,"y":336,"label":"B2","state":{"on":false}}, {"type":"Toggle","id":"dev6","x":112,"y":400,"label":"B3","state":{"on":false}}, {"type":"Toggle","id":"dev7","x":112,"y":280,"label":"B1","state":{"on":false}}, {"type":"Toggle","id":"dev8","x":112,"y":216,"label":"B0","state":{"on":false}}, {"type":"DC","id":"dev9","x":0,"y":280,"label":"DC"}, {"type":"Toggle","id":"dev10","x":48,"y":64,"label":"A","state":{"on":false}}, {"type":"Toggle","id":"dev11","x":48,"y":0,"label":"Cin","state":{"on":false}}, {"type":"Toggle","id":"dev12","x":48,"y":120,"label":"B","state":{"on":false}}, {"type":"HalfAdder","id":"dev13","x":96,"y":88,"label":"HalfAdder1"}, {"type":"HalfAdder","id":"dev14","x":152,"y":16,"label":"HalfAdder2"}, {"type":"OR","id":"dev15","x":240,"y":80,"label":"OR"}, {"type":"LED","id":"dev16","x":304,"y":16,"label":"S"}, {"type":"LED","id":"dev17","x":304,"y":80,"label":"Cout"}, {"type":"HalfAdder","id":"dev18","x":184,"y":184,"label":"HalfAdder"}, {"type":"FullAdder","id":"dev19","x":184,"y":248,"label":"FullAdder1"}, {"type":"LED","id":"dev20","x":304,"y":184,"label":"S0"}, {"type":"FullAdder","id":"dev21","x":184,"y":320,"label":"FullAdder2"}, {"type":"FullAdder","id":"dev22","x":184,"y":392,"label":"FullAdder3"}, {"type":"LED","id":"dev23","x":304,"y":416,"label":"Cout"}, {"type":"LED","id":"dev24","x":304,"y":240,"label":"S1"}, {"type":"LED","id":"dev25","x":304,"y":304,"label":"S2"}, {"type":"LED","id":"dev26","x":304,"y":360,"label":"S3"} ], "connectors":[ {"from":"dev1.in0","to":"dev9.out0"}, {"from":"dev2.in0","to":"dev9.out0"}, {"from":"dev3.in0","to":"dev9.out0"}, {"from":"dev4.in0","to":"dev9.out0"}, {"from":"dev5.in0","to":"dev9.out0"}, {"from":"dev6.in0","to":"dev9.out0"}, {"from":"dev7.in0","to":"dev9.out0"}, {"from":"dev8.in0","to":"dev9.out0"}, {"from":"dev10.in0","to":"dev0.out0"}, {"from":"dev11.in0","to":"dev0.out0"}, {"from":"dev12.in0","to":"dev0.out0"} ] }

第６節　集積回路

　すべての演算(論理)回路はAND, OR, NOTの3種類の素子から組み立てられることはわかった。では、CPUの演算回路は、これら3種類の素子を多量にかつ複雑に配置してつないでいるのだろうか。実はこれらの素子は、１種類のスイッチ素子から組み立てられる。
　CPUで 0, 1 は、電流の ON(1) と OFF(0) で表される。そこで、一方の電流の ON, OFF によって、もう一方の電流の ON, OFFを制御するスイッチがあれば、次ページの問からも分かるように、任意の論理回路が構成できる。歴史的には、このようなスイッチにリレースイッチ、真空管、トランジスタ(半導体)などが使われてきた（第１講第１節）。
　このように、スイッチ素子のつなぎ方だけを変えることで、AND, OR, NOT素子が実現でき、ひいては任意の演算回路が実現できる。したがってきわめて単純化して言えば、スイッチ素子を格子状に並べておいて、その間の配線を工夫すれば演算回路(CPU)が実現できる。半導体を使って一枚の基板上にスイッチ素子を配線とともに直接作りこもうというのが集積回路のアイディアである。集積回路は格子間隔を細かくすればするほど小さくする(集積度を上げる)ことができる。

コラム．ティンカートイ コンピュータ
Tinkertoy Computer 　電子(電気)部品でなくとも、一方のON/OFFで他方のON/OFFが制御できればコンピュータを作れる。ティンカートイ(tinkertoy、木組みのおもちゃ)で、三目並べをするコンピュータをどうやって作るかに関するDewdneyの記事(SCIENTIFIC AMERICAN October 1989)を見よ。
問７．６．AND、OR、NOT素子の設計：シミュレータを使って1～３を確かめ４に答えよ。 （ヒント）
  1. スイッチ素子は、Xに電圧がかかる(X=1)とYとZが遮断され、X=0のときYとZがつながって電流が流れる
  2. Yに電圧をかける(Y＝1)と、X＝1のときZ=0でX＝0のときZ=1だから、NOTの働きをする
  3. スイッチ素子を直列につないで右の￢につなぐと、￢(￢X∧￢Y)=X∨YなのでORができる
  4. スイッチ素子を使ってAND素子を構成するつなぎ方を記述せよ
    ヒント：スイッチ素子の働きは￢X∧Yなので、Switch2のX端子に￢Xをつなぐ。

{ "width":450, "height":320, "showToolbox":true, "toolbox":[ {"type":"DC"}, {"type":"LED"}, {"type":"Toggle"}, {"type":"Switch"}, {"type":"NOT"}, {"type":"AND"}, {"type":"OR"} ], "devices":[ {"type":"Toggle","id":"dev0","x":48,"y":0,"label":"X","state":{"on":false}}, {"type":"DC","id":"dev1","x":0,"y":184,"label":"DC"}, {"type":"Toggle","id":"dev2","x":56,"y":216,"label":"X","state":{"on":false}}, {"type":"DC","id":"dev3","x":0,"y":248,"label":"DC"}, {"type":"Toggle","id":"dev4","x":56,"y":272,"label":"Y","state":{"on":false}}, {"type":"Toggle","id":"dev5","x":40,"y":104,"label":"X","state":{"on":false}}, {"type":"Toggle","id":"dev6","x":88,"y":104,"label":"Y","state":{"on":false}}, {"type":"Switch","id":"dev7","x":80,"y":152,"label":"Switch"}, {"type":"LED","id":"dev8","x":184,"y":8,"label":"LED"}, {"type":"DC","id":"dev9","x":0,"y":24,"label":"DC"}, {"type":"Toggle","id":"dev10","x":48,"y":48,"label":"Y","state":{"on":false}}, {"type":"Switch","id":"dev11","x":96,"y":16,"label":"Switch"}, {"type":"LED","id":"dev12","x":304,"y":96,"label":"￢X"}, {"type":"Switch","id":"dev13","x":224,"y":96,"label":"Switch"}, {"type":"Toggle","id":"dev14","x":184,"y":56,"label":"X","state":{"on":false}}, {"type":"DC","id":"dev15","x":136,"y":80,"label":"DC"}, {"type":"LED","id":"dev16","x":304,"y":176,"label":"X∨Y"}, {"type":"Switch","id":"dev17","x":224,"y":176,"label":"Switch"}, {"type":"Switch","id":"dev18","x":152,"y":128,"label":"Switch"}, {"type":"Switch","id":"dev19","x":112,"y":240,"label":"Switch1"}, {"type":"Switch","id":"dev20","x":200,"y":264,"label":"Switch2"}, {"type":"LED","id":"dev21","x":304,"y":264,"label":"X∧Y"} ], "connectors":[ {"from":"dev0.in0","to":"dev9.out0"}, {"from":"dev2.in0","to":"dev3.out0"}, {"from":"dev4.in0","to":"dev3.out0"}, {"from":"dev5.in0","to":"dev1.out0"}, {"from":"dev6.in0","to":"dev1.out0"}, {"from":"dev7.in0","to":"dev5.out0"}, {"from":"dev7.in1","to":"dev1.out0"}, {"from":"dev8.in0","to":"dev11.out0"}, {"from":"dev10.in0","to":"dev9.out0"}, {"from":"dev11.in0","to":"dev0.out0"}, {"from":"dev11.in1","to":"dev10.out0"}, {"from":"dev12.in0","to":"dev13.out0"}, {"from":"dev13.in0","to":"dev14.out0"}, {"from":"dev13.in1","to":"dev15.out0"}, {"from":"dev14.in0","to":"dev15.out0"}, {"from":"dev16.in0","to":"dev17.out0"}, {"from":"dev17.in0","to":"dev18.out0"}, {"from":"dev17.in1","to":"dev1.out0"}, {"from":"dev18.in0","to":"dev6.out0"}, {"from":"dev18.in1","to":"dev7.out0"} ] }