問２．８．

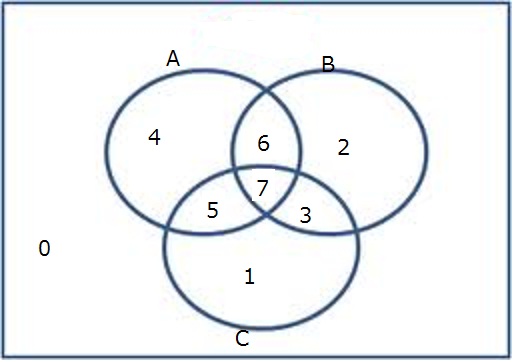
１．右図は、集合A、B、C のベン図である。0 から 7 までの番号を付けた集合(条件)を表す集合演算式(論理式)を下表の空欄に記述せよ。 また、A の欄には、対応する集合が A に含まれない場合は 0 を A に含まれる場合は 1 を入れ、B、C の欄にも同様に記入せよ。 ＞∩や∧の読みは「あんど」、∪や∨の読みは「おあ」でかな漢字変換できます。各番号の領域が A、B、C の各々に属す・属さないにしたがって、１・０ の値や論理式、集合演算式を記述する。例を参考に考えてみよう。 領域番号 集合演算式 A B C 論理式 0 A~∩B~∩C~ 0 0 0 ￢A∧￢B∧￢C 1 2 3 A~∩B∩C 0 1 1 ￢A∧B∧C 4 5 6 A∩B∩C~ 1 1 0 A∧B∧￢C 7 ２．集合(条件)A、B、Cで区分けされる集合(条件)はすべて、0から7までの番号づけられた集合(条件)の和集合(論理和)で表されるから、A、B、Cから∩、∪、~(∧、∨、￢)の組み合わせで表される。 １)１と３と５の和集合(論理和)を表す集合演算式(および論理式)を求めよ。 ＞１と３と５の領域を表す集合演算式（論理式）を∪（∨）でつなげればよい。 ２)１と３と５の和集合(論理和)を表す集合演算式(および論理式)をできるだけ簡単な形で表せ。 ＞１と３と５を合わせた領域は C から A と B の共通部分を除いた領域です ３．5集合ベン図では、全体集合がいくつの集合(領域)に分割されているか。 ＞数えるのは面倒です。３集合ベン図では２×２×２＝８個の領域に分割されていることに注目します。