概要
・正則（正規）言語の諸性質を学びます・言語が正則言語であるための必要十分条件を学びます
・非正則言語の例を示します
・正則言語に対する正則表現を求めます
この授業では、オートマトンの動作や文法の導出のデモにJFLAPを利用します
コラム．正則か正規か
数学分野での訳語としては regular：正則、normal：正規 が定着している。ここでは、regular language を正則言語と呼んでいるが、正規言語という言い方も一般的である。
有限オートマトン（FA）
|
- 状態の有限集合 $Q$
- 入力アルファベット $\Sigma$
- 遷移の集合 $\delta\subseteq Q\times\Sigma^?\times Q$
- 開始状態 $q_0\in Q$
- 受理状態の集合 $F\subseteq Q$
例．有限オートマトンを図示するには、右図のように、状態を〇で囲み、開始状態に$\rhd$を付け、受理状態を◎で囲み、遷移$(p,a,q)\in\delta$をラベル付き矢印$\circled{p}\labelarrow{a}\circled{q}$で表す。
$\delta\subseteq Q\times\Sigma^?\times Q$ に対し $\delta^*\subseteq Q\times\Sigma^*\times Q$ を帰納的に以下で定義し、
- $q\in Q\drarrow (q,\varepsilon,q)\in \delta^*$
- $(p,\vect{v},q)\in \delta^* \wedge a{\in}\Sigma \wedge (q,a,r){\in}\delta \drarrow (p,\vect{v}a,r)\in \delta^*$
- $(p,\vect{w},q)\in \delta^* \wedge (q,\varepsilon,r)\in \delta \drarrow (p,\vect{w},r)\in \delta^*$
与えられた$\vect{w}$に対し$(p,\vect{w},q)\in \delta^*$を求めるには、$\vect{w}=\varepsilon$ の場合には1.を基礎に3.を繰返し、$\vect{w}=\vect{v}a,\ a{\in}\Sigma$ の場合には$\vect{v}$に対する2.を基礎に3.を繰返す。
$\delta^*(q_0,\vect{w})\cap F\ne\emptyset$のとき、$M$は$\vect{w}$を受理(認識)するといい、$\mathcal{L}(M):=\{\vect{w} \mid \delta^*(q_0,\vect{w})\cap F\ne\emptyset\}\subseteq \Sigma^*$ を$M$が認識(受理)する言語という。
時点表示
オートマトンの動作状況の表示を一般に時点表示という。オートマトンのある動作で時点表示が$\alpha$から$\beta$に移ることを$\alpha\vdash\beta$と表し、$\vdash$の$0$回以上の繰返し$\VDASH{}{*}$を帰納的に 1.$\alpha\VDASH{}{*}\alpha,$ 2.$\alpha\VDASH{}{*}\beta\vdash\gamma \drarrow \alpha\VDASH{}{*}\gamma$ で定義する。
有限オートマトンの時点表示は 状態と未読文字列の連接 で表され、$(p,a,q)\in \delta \drarrow pa\vect{w}\vdash q\vect{w}$ である。このとき、$p\vect{w}\VDASH{}{*}q \darrow{\rightarrow}{\leftarrow} (p,\vect{w},q)\in \delta^* \darrow{\rightarrow}{\leftarrow} q\in \delta^*(p,\vect{w})$
が成立つ。特に、$\varepsilon$遷移 $(q,\varepsilon,r)\in \delta$ は無入力による状態遷移を意味し、
$(p,\vect{w},q){\in}\delta^*\wedge (q,\varepsilon,r){\in}\delta \drarrow (p,\vect{w},r){\in}\delta^*$ であり、
$(q,\varepsilon,r){\in}\delta \drarrow q\vect{v} \vdash r\vect{v}$ である。
例．右図の有限オートマトンで、入力$1001$に対する時点表示列(複数ある)の$1$例は、
$q_01001\vdash q_0001\vdash q_001\vdash q_11\vdash q_2$
より、$q_01001\VDASH{}{*}q_2$で、$1001$は受理される。
パズル．右上図の有限オートマトンについて
①$1001$に対する可能な動作列をすべて調べよ 答
②どのような文字列を受理するか
オートマトンの動作状況の表示を一般に時点表示という。オートマトンのある動作で時点表示が$\alpha$から$\beta$に移ることを$\alpha\vdash\beta$と表し、$\vdash$の$0$回以上の繰返し$\VDASH{}{*}$を帰納的に 1.$\alpha\VDASH{}{*}\alpha,$ 2.$\alpha\VDASH{}{*}\beta\vdash\gamma \drarrow \alpha\VDASH{}{*}\gamma$ で定義する。
有限オートマトンの時点表示は 状態と未読文字列の連接 で表され、$(p,a,q)\in \delta \drarrow pa\vect{w}\vdash q\vect{w}$ である。このとき、
$(p,\vect{w},q){\in}\delta^*\wedge (q,\varepsilon,r){\in}\delta \drarrow (p,\vect{w},r){\in}\delta^*$ であり、
$(q,\varepsilon,r){\in}\delta \drarrow q\vect{v} \vdash r\vect{v}$ である。
例．右図の有限オートマトンで、入力$1001$に対する時点表示列(複数ある)の$1$例は、
$q_01001\vdash q_0001\vdash q_001\vdash q_11\vdash q_2$より、$q_01001\VDASH{}{*}q_2$で、$1001$は受理される。
パズル．右上図の有限オートマトンについて
①$1001$に対する可能な動作列をすべて調べよ 答
②どのような文字列を受理するか
有限オートマトンの例
渡船パズル有限オートマトンの例として、パズルを考えてみよう。狼と羊を連れキャベツの籠を持つ農夫が小舟で川を渡りたいが、
- 舟は農夫の他１頭(籠)しか乗れず
- 農夫がいないと、オオカミはヤギを食べ、ヤギはキャベツを食べる。
このパズルは有限オートマトンで表現して解ける。"状態"を両岸にいる(ある)ものの配置とし縦棒で区切って表し、"遷移"を農夫が小舟で運ぶもの w(狼), g(羊), c(キャベツ)、f(無し)で表すと右図のようになる。(狼が羊を食べたり、羊がキャベツを食べる状態への遷移は除く)
このとき、開始状態${\rhd}\circled{\text{fwgc|}}$から受理状態$\dcircled{\text{|fwgc}}$へ至る遷移列が、パズルの解になる。
パズル．農夫パズルの解を２つ示せ。
$M{=}(Q,\Sigma,\delta,q_0,F)$に対し $\vect{v}\vect{w}\in \mathcal{L}(M)\darrow{\rightarrow}{\leftarrow} \exists p{\in}\delta^*(q_0,\vect{v})\ \ \delta^*(p,\vect{w})\cap F\ne\emptyset$ より
$\mathcal{L}(M,p):=\{\vect{v}\mid p\in\delta^*(q_0,\vect{v})\}$：初期状態から$p$に至る入力列の集合
$\mathcal{L}(p,M):=\{\vect{w}\mid \delta^*(p,\vect{v})\cap F\ne\emptyset\}$：$p$から受理状態に至る入力列の集合
と定義すれば、$\mathcal{L}(M)=\bigcup_{p\in Q}\mathcal{L}(M,p)\mathcal{L}(p,M)$が成立つ。以下の2例はそれぞれ$\mathcal{L}(M,p),\ \mathcal{L}(p,M)$に着目して設計される。
3で割切れる2進数
$3$で割切れる$2$進数を受理する有限オートマトン$M$を考えてみよう。
基本的なアイディアは、3で割った余りを状態$q_0,q_1,q_2$で区別し、
$\vect{w}\in\mathcal{L}(M,q_k)\darrow{\rightarrow}{\leftarrow}\,$2進数$\vect{w}$の値を$3$で割った余りが$k$
とすることである。これができれば、開始状態と受理状態をともに$q_0$とした有限オートマトンは3で割切れる2進数を受理する。
パズル．上のアイディアに沿って、有限オートマトンを描け。
ヒント．$2$進数$\vect{w}$の値を$[\vect{w}]_2$で表すと、$[\vect{w}0]_2=2[\vect{w}]_2,\ [\vect{w}1]_2=2[\vect{w}]_2+1$。
答 JFLAPファイル
符号付小数
符号付小数(整数を含む)を認識するFA $M$ を構成するには状態 $q$ を $\mathcal{L}(q,M)$ で意味づけるとよい。
$\mathcal{L}(q_0,M)={}$符号付小数
$\mathcal{L}(q_1,M)={}$符号無小数
$\mathcal{L}(q_4,M)={}$小数部
とおくと、整数部は 0 か、1～9 で始まる 0～9 の列で、小数部は 1～9 で終わる 0～9 の列なので、上のFAを得る。（整数は$q_2,q_3$で受理される）
問．上のFAを 0 は受理されるが +0 や -0 は受理されないように改良せよ。
$3$で割切れる$2$進数を受理する有限オートマトン$M$を考えてみよう。
基本的なアイディアは、3で割った余りを状態$q_0,q_1,q_2$で区別し、
$\vect{w}\in\mathcal{L}(M,q_k)\darrow{\rightarrow}{\leftarrow}\,$2進数$\vect{w}$の値を$3$で割った余りが$k$
とすることである。これができれば、開始状態と受理状態をともに$q_0$とした有限オートマトンは3で割切れる2進数を受理する。
パズル．上のアイディアに沿って、有限オートマトンを描け。
ヒント．$2$進数$\vect{w}$の値を$[\vect{w}]_2$で表すと、$[\vect{w}0]_2=2[\vect{w}]_2,\ [\vect{w}1]_2=2[\vect{w}]_2+1$。
答 JFLAPファイル
符号付小数符号付小数(整数を含む)を認識するFA $M$ を構成するには状態 $q$ を $\mathcal{L}(q,M)$ で意味づけるとよい。
$\mathcal{L}(q_0,M)={}$符号付小数
$\mathcal{L}(q_1,M)={}$符号無小数
$\mathcal{L}(q_4,M)={}$小数部
とおくと、整数部は 0 か、1～9 で始まる 0～9 の列で、小数部は 1～9 で終わる 0～9 の列なので、上のFAを得る。（整数は$q_2,q_3$で受理される）
問．上のFAを 0 は受理されるが +0 や -0 は受理されないように改良せよ。
決定性有限オートマトン（DFA）
有限オートマトン$M=(Q,\Sigma,\delta,q_0,F)$は次の条件を満たすとき決定性有限オートマトン(DFA, Determinisitic Finite Automaton)1)という。- $\delta\subseteq Q\times\Sigma\times Q$：$\varepsilon$遷移を持たない
- $(p,a)\in Q\times\Sigma\drarrow |\delta^*(p,a)|=1$：状態と文字の組に対し遷移先の状態が常に1つ定まる
このとき明らかに、$(p,\vect{w})\in Q\times\Sigma^*$ に対し $|\delta^*(p,\vect{w})|=1$ だから、$\{q\}$と$q$を同一視し、$\delta^*(p,\vect{w})=\{q\}$ を $\delta^*(p,\vect{w})=q$ と表す。したがって、決定性有限オートマトンでは $\mathcal{L}(M)=\{w\mid \delta^*(q_0,\vect{w})\in F\}$ と書ける。
また、決定性を問題にするときは、有限オートマトンを非決定性有限オートマトン(NFA, Nondeterministic Finite Automaton)2)ということもある。
例．3で割切れる2進数の答で示したFAはDFAである。農夫パズルのFAは、(状態,文字)の組に対する遷移先は、高々1状態だが、ない場合もあり、DFAでない。符号付小数のFAは$\varepsilon$遷移を持ち、$\delta^*(q_4,1)=\{q_4,q_5\}$でもあるのでDFAでなく、最初の例$M_1$は、$\varepsilon$遷移はないが、$\delta^*(q_0,0)=\{q_0,q_1\}$よりDFAでない。
問．DFA$M=(Q,\Sigma,\delta,q_0,F)$に対し。$M^\complement:=(Q,\Sigma,\delta,q_0,Q-F)$ とおけば、$\mathcal{L}(M^\complement)=\mathcal{L}(M)^\complement=\Sigma^*-\mathcal{L}(M)$ であることを示せ。
注．1) DFAの定義において、渡船パズルのFAのように遷移先の状態がないことを許す場合もある。その場合は死状態（そこでループする非受理状態）への遷移を省略していると考えればよい
2) 状態と文字の組に対し複数の遷移を許すものをNFA、$\varepsilon$ラベルの遷移まで許すものを$\varepsilon$NFAと区別することもある。このテキストでのFAは$\varepsilon$NFAである。
FAからDFAへの変換
$L\subseteq \Sigma^*,\ \vect{w}\in\Sigma^*$に対し $\vect{w}\backslash L:=\{\vect{v}\mid \vect{w}\vect{v}\in L\}$ と定義する。定理． $L\subseteq \Sigma^*$ がFAで認識されるならば、
- $\{\vect{w}\backslash L\mid \vect{w}\in\Sigma^*\}$は有限集合
- $L$は、DFA $L_D:=(\{\vect{w}\backslash L\mid \vect{w}\in\Sigma^*\},\Sigma,\varDelta,L,\{\vect{w}\backslash L \mid \vect{w}\in L\})$、$\varDelta:=\{(\vect{w}\backslash L,a,(\vect{w}a)\backslash L)\mid \vect{w}\in\Sigma^*,\ a\in\Sigma\}$ で認識される
- 上の$L_D$は、$L$を受理するDFA中、状態数最少である。
2. $(\vect{w}\vect{v})\backslash L{=}\vect{v}\backslash(\vect{w}\backslash L)$より、$\mathcal{L}_D$はDFAで$\vect{w}\backslash L{=}\mathcal{L}(\vect{w}\backslash L,L_D)$。故に$\mathcal{L}(L_D){=}L$。
3. 1.で$M$がDFAなら、$\forall \vect{w}\ |\delta^*(q_0,\vect{w})|=1$で$\vect{w}\backslash L=\mathcal{L}(\delta^*(q_0,\vect{w}),M)$だから、$|\{\vect{w}\backslash L\mid \vect{w}\in\Sigma^*\}|\le |Q|$
与えられたFAに等しい最小(状態数最少)のDFAを構成する手順を考えてみよう。
FAからDFAの構成
$M{=}(Q,\Sigma,\delta,q_0,F)$に対し $Q_\vect{w}{:=}\delta^*(q_0,\vect{w}),$ $\varDelta{:=}\{(Q_\vect{w},a,Q_{\vect{w}a})\mid \vect{w}{\in}\Sigma^*,a{\in}\Sigma\},$ $M_D{:=}(\{Q_\vect{w}\mid \vect{w}{\in}\Sigma^*\},\Sigma,\varDelta,Q_\varepsilon,\{Q_\vect{w} \mid Q_\vect{w}{\cap}F{\ne}\emptyset\})$とおく。$\{Q_\vect{w}\mid \vect{w}{\in}\Sigma^*\}\subseteq\vect{2}^Q$は有限集合で$M_D$はDFA。$\varDelta^*(Q_\varepsilon,\vect{w}){=}Q_\vect{w}{=}\delta^*(q_0,\vect{w})$より$\mathcal{L}(M_D)=\{\vect{w} \mid \varDelta^*(Q_\varepsilon,\vect{w}){\cap}F{\ne}\emptyset\}=\{\vect{w} \mid \delta^*(q_0,\vect{w}){\cap}F{\ne}\emptyset\}=\mathcal{L}(M)$。
実際に$M$から$M_D$を構成する際、$Q_\vect{w}$はその帰納的定義
- $q_0 \in Q_{\varepsilon}$
- $p{\in}Q_\vect{v} \wedge a{\in}\Sigma \wedge (p,a,q){\in}\delta \drarrow q{\in}Q_{\vect{v}a}$
- $p{\in}Q_\vect{w} \wedge (p,\varepsilon,q){\in}\delta \drarrow q{\in}Q_{\vect{w}}$
例．符号と小数点を含む$2$進数を認識するFA(左図)とDFA(右図)。右図では$Q_\vect{w}$を改めて$q_i$で表し($q_0:Q_{\varepsilon},\ q_1:Q_{1},\ q_2:Q_{.},\ q_3:Q_{+},\ q_4:Q_{1.},\ q_5:Q_{.1}$)、四角内にFA(左図)の状態$q_k\in Q_\vect{w}$の番号$k$を表示している。また、死状態$Q_\vect{w}=\emptyset$とそこへの遷移を省略している。
$n$状態のFAからDFAを構成する上記の方法(Subset Construction)は一般に、$2^n$状態のDFAを構成する。実際にそのオーダーの状態数が必要な例として、末尾から$n$番目が$1$である$\Sigma=\{0,1\}$上の言語 $\Sigma^*\{1\}\Sigma^{n-1}$ がある。$n=4$の例を下図に示すが、DFAの状態は $\{\{q_0\}\cup P\mid P\subseteq \{q_1,q_2,q_3,q_4\}\}$ となる。
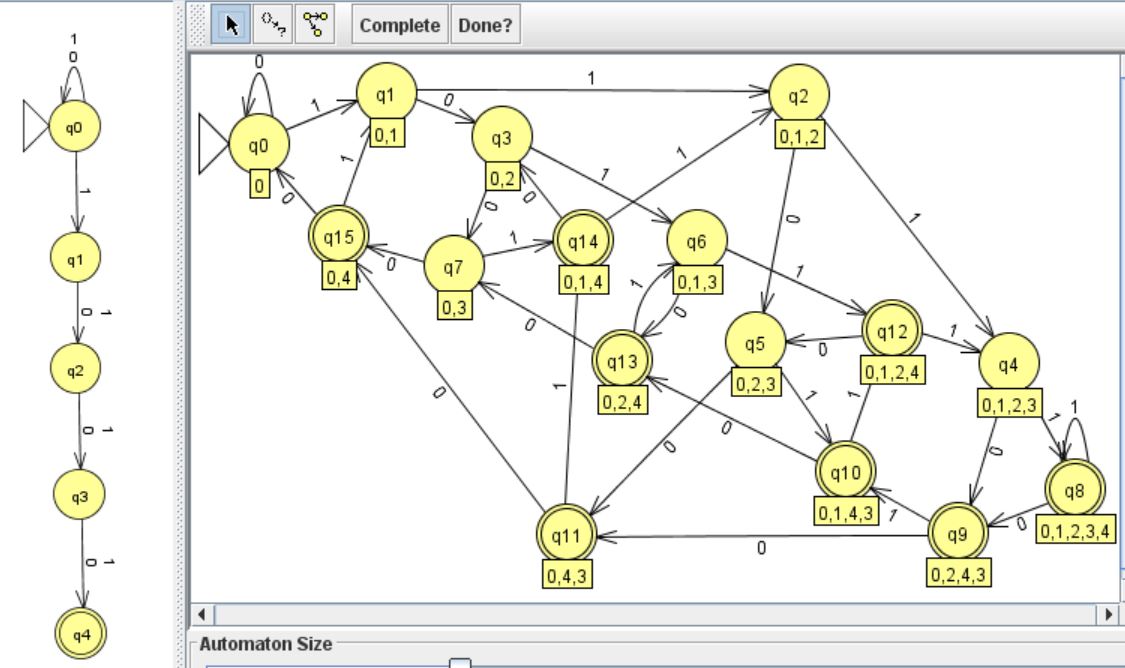
パズル．$\Sigma:=\{0,1\},\ L_n:=\Sigma^*\{1\}\Sigma^{n-1}$とおく。
パズル．$\Sigma:=\{0,1\},\ L_n:=\Sigma^*\{1\}\Sigma^{n-1}$とおく。
- $\vect{v},\vect{w}\in\Sigma^n$に対し、$\vect{v}\ne \vect{w} \Rightarrow (\vect{v}\backslash L_n)\cap \{0\}^*\ne (\vect{w}\backslash L_n)\cap \{0\}^*$ を示せ。
- $\vect{w}\in\Sigma^n,\ \vect{u},\vect{v}\in\Sigma^*$に対し $\vect{u}\vect{w}\backslash L_n=\vect{v}\vect{w}\backslash L_n$ を示せ。
- $|\{\vect{w}\backslash L_n\mid \vect{w}\in\Sigma^*\}|=|\Sigma^n|=2^n$を示せ。
ところで、FA$M$から作成したDFA$M_D$は、$\mathcal{L}(M)$を認識する最小のDFAとは限らない。実際、$Q_\vect{w}{\ne}Q_{\vect{w}'} \wedge \mathcal{L}(Q_\vect{w},M){=}\mathcal{L}(Q_{\vect{w}'},M)$となる可能性がある。
DFAの最小化
DFA $M{=}(Q,\Sigma,\delta,q_0,F)$ の最小化の問題を考えよう。$Q$の同値類を $[p]:=\{q\mid \mathcal{L}(p,M){=}\mathcal{L}(q,M)\}$ で定義すれば、$\forall a{\in}\Sigma\, \delta^*(p,a){\in}[\delta^*(q,a)]\rightleftarrows p{\in}[q],$ $[p]{\subseteq}F \vee [p]{\subseteq}F^\complement$ が成立つ。よって$\Delta:=\{([q],a,[\delta^*(q,a)]\mid q{\in}Q,a{\in}\Sigma\}$とおいた $M'=(\{[\delta(q_0,\vect{w})]\mid \vect{w}{\in}\Sigma^*\},\Sigma,\Delta,[q_0],\{[q]\mid q{\in}F\})$ は$M$と等しい最小DFAである。
DFA $M=(Q,\Sigma,\delta,q_0,F)$から最小DFA$M'$を構成するには、開始状態から到達不能な状態を除き、関係$p\not\in [q]$を再帰的に次で求めればよい。状態$p\ne q$に対し
DFA（左図）とその最小化（右図）：左図の状態q3は開始状態から到達不能なので除かれる(中央図)。
DFAの最小化
DFA $M{=}(Q,\Sigma,\delta,q_0,F)$ の最小化の問題を考えよう。$Q$の同値類を $[p]:=\{q\mid \mathcal{L}(p,M){=}\mathcal{L}(q,M)\}$ で定義すれば、$\forall a{\in}\Sigma\, \delta^*(p,a){\in}[\delta^*(q,a)]\rightleftarrows p{\in}[q],$ $[p]{\subseteq}F \vee [p]{\subseteq}F^\complement$ が成立つ。よって$\Delta:=\{([q],a,[\delta^*(q,a)]\mid q{\in}Q,a{\in}\Sigma\}$とおいた $M'=(\{[\delta(q_0,\vect{w})]\mid \vect{w}{\in}\Sigma^*\},\Sigma,\Delta,[q_0],\{[q]\mid q{\in}F\})$ は$M$と等しい最小DFAである。
DFA $M=(Q,\Sigma,\delta,q_0,F)$から最小DFA$M'$を構成するには、開始状態から到達不能な状態を除き、関係$p\not\in [q]$を再帰的に次で求めればよい。状態$p\ne q$に対し
- $|\{p,q\}{\cap}F|=1 \drarrow p \not\in [q]$
- ある$a\in\Sigma$に対し$\delta(p,a)\not\in[\delta(q,a)] \drarrow p\not\in[q]$
|
 |
正則文法（RG）
文法 $G=(\Gamma,\Sigma,P,S)$は、- 非終端アルファベット $\Gamma$
- 終端アルファベット $\Sigma,\ \ \Sigma\cap\Gamma=\emptyset$
- 規則の有限集合 $P$
- 開始記号 $S\in \Gamma$
文法の規則 $\alpha\to\beta$ を適用して、文形式 $\xi\alpha\zeta\in(\Sigma\cup\Gamma)^*$ を $\xi\beta\zeta\in(\Sigma\cup\Gamma)^*$ に置き換えることを導出といい、$\xi\alpha\zeta \Rightarrow \xi\beta\zeta$ と表す。導出$\Rightarrow$の$0$回以上の繰返し$\overset{*}\Rightarrow$を帰納的に 1.$\xi\overset{*}\Rightarrow \xi$、2.$\xi\overset{*}\Rightarrow\eta\Rightarrow\zeta \drarrow \xi\overset{*}\Rightarrow \zeta$ で定義する。
$\alpha\in(\Sigma\dot\cup\Gamma)^*$に対し$\alpha\overset{*}\Rightarrow \vect{w}\in \Sigma^*$ となるとき、文法$G$で$\alpha$が終端記号列$\vect{w}$を生成(導出)するといい、$\mathcal{L}(\alpha,G):=\{\vect{w}\mid \alpha\overset{*}\Rightarrow \vect{w}\in\Sigma^*\}$を$G$で$\alpha$が生成する言語、$\mathcal{L}(G):=\mathcal{L}(S,G)$ を$G$が生成する言語という。
正則文法では、規則の形は $A\to \vect{w}B$（$\vect{w}\in \Sigma^*,\ B\in \Gamma^?$）なので、導出列は
また、$\mathcal{L}(A,G),\ A{\in}\Gamma$は同時帰納的に、1.$A{\to}\vect{w}\in P \drarrow \vect{w}\in \mathcal{L}(A,G)$, 2.$A{\to}\vect{w}B\in P \wedge \vect{v}\in \mathcal{L}(B,G)\drarrow \vect{wv}\in \mathcal{L}(A,G)$でも定義できる。
例．RG S→1S|0S|0A、A→1 の導出例：$S\Rightarrow 1S\Rightarrow 10A\Rightarrow 101$
パズル．①上の文法が文字列1001を生成する($S$から導出される)ことを示せ
②上の文法で生成されるのはどのような文字列か。
RGとFAの相互変換
定理．正則文法は、規則の右辺を $aB,\ \varepsilon$（$a\in \Sigma^?,\ B\in \Gamma$）の形に制限しても、その生成能力が変わらない。証明．規則 $A\to a_1a_2\cdots a_kB,\ k\ge 1,\ B\in\Gamma^?$ を$(k+1)$個の規則
定理の形の正則文法 $G=(\Gamma,\Sigma,P,S)$ は、規則の次の解釈により有限オートマトン $M=(\Gamma,\Sigma,\delta,S,\Lambda)$ と見なせ、逆も成立つ。
定理．次の同値な$３$条件を満たす言語を正則言語という。
① DFAで認識される$\darrow{\rightarrow}{\leftarrow}$② FAで認識される$\darrow{\rightarrow}{\leftarrow}$③ RGで生成される
|
|
正則言語の諸性質
定理．．$L_1,L_2\subseteq \Sigma^*$が正則言語ならば、以下も正則言語である。① $L_1\cup L_2$ ② $L_1\cap L_2$ ③ $L_1^\complement$ ④ $L_1^R$ ⑤ $L_1L_2$ ⑥ $L_1^*$
準同型写像$h$に対し、⑦ $h(L_1)$ ⑧ $h ^{-1}(L_1):=\{\vect{w}\mid h(\vect{w}){\in}L_1\}$
略証．③$L_1$を認識するDFAで状態の受理・非受理を入替えればよい。
以下、$L_1,\ L_2$を生成するRG$G_1,\ G_2$の非終端記号は互いに素であるとし、開始記号をそれぞれ$S_1,\ S_2$とする。
①規則$S{\to} S_1｜S_2$ を追加すれば、$S$から生成される。
②$L_1\cap L_2=(L_1^\complement\cup L_2^\complement)^\complement$より明らか。
⑤$G_1$の規則$A{\to}\vect{w}$を$A{\to}\vect{w}S_2$に入換えれば$S_1$から生成される。
⑥$G_1$の規則$A{\to}\vect{w}$を$A{\to}\vect{w}S_1$に入換え$S_1{\to}\varepsilon$を加えれば$S_1$から生成される。
⑦$G_1$の規則$A{\to}\vect{w}B$を$A{\to}h(\vect{w})B$に入換えれば$S_1$から生成される。
⑧$L_1$を認識するDFA$M$で、遷移$\delta$を$\{(q,a,\delta^*(q,h(a))) \mid q{\in}Q,a{\in}\Sigma\}$に置き換える。
パズル．$L$が正則集合ならその反転$L^R$も正則集合であることを示せ。
反復補題．$L\ (\subseteq\Sigma^*)$ が正則言語ならば、$L$の十分長い文字列は$\vect{w}=\vect{x}\vect{y}\vect{z},\ \vect{y}\ne\varepsilon$と書け、$\{\vect{x}\}\{\vect{y}\}^*\{\vect{z}\}\subseteq L$。証明．$L$を認識するDFA$M=(Q,\Sigma,\delta,q_0,F)$において、$|\vect{w}|\ge|Q|$ならば、$\vect{w}$による遷移中に同じ状態$q$が現れる(鳩ノ巣原理)から$\vect{w}=\vect{x}\vect{y}\vect{z},\ \vect{y}\ne\varepsilon$と分割でき、$\delta^*(q_0,\vect{x})=\delta^*(q_0,\vect{x}\vect{y})$が成立つ。このとき、$\vect{w}\in L$ならば$\{\vect{x}\}\{\vect{y}\}^*\{\vect{z}\}\subseteq L$。
応用．$L=\{0^n1^n|n\in\mathbb{N}\}$は正則言語ではない。
証明1．$0^k\backslash L=\{0^n1^{n+k}|n\in\mathbb{N}\}$は$k$毎に異なり、$\{\vect{w}\backslash L|\vect{w}\in\{0,1\}^*\}$は有限集合でない。
証明2．$L$の十分長い文字列 $\vect{x}\vect{y}\vect{z}$ に対し、$\varepsilon\ne \vect{y}=0^j,\ 0^j1^k,\ 1^k$ のどの場合も $\vect{x}\vect{y}^2\vect{z}\not\in L$ であるから、反復補題に矛盾する。
正則言語の判定問題
有限オートマトン、正則文法、正規表現等で与えられた正則言語に関わる様々な判定問題が判定可能であることを示す。
定理．正則言語$L,L'\subseteq\Sigma^*$と語$\vect{w}\in\Sigma^*$に対し、次が成立つか否かを判定するアルゴリズムが存在する。
１．$L=\emptyset,\ L=\Sigma^*,\ L\subseteq L'$
２．$\vect{w}\in L$
証明．$L=\emptyset$か否かは$L$を認識するDFAに開始状態から受理状態へ至る路があるか否かで判定できる。以下、$L=\Sigma^*\darrow{\rightarrow}{\leftarrow}L^\complement=\emptyset,\ L\subseteq L'\darrow{\rightarrow}{\leftarrow}L-L'=\emptyset,\ \vect{w}\in L\darrow{\rightarrow}{\leftarrow}\{\vect{w}\}-L=\emptyset$
であるから、いずれも判定可能である。
証明1．$0^k\backslash L=\{0^n1^{n+k}|n\in\mathbb{N}\}$は$k$毎に異なり、$\{\vect{w}\backslash L|\vect{w}\in\{0,1\}^*\}$は有限集合でない。
証明2．$L$の十分長い文字列 $\vect{x}\vect{y}\vect{z}$ に対し、$\varepsilon\ne \vect{y}=0^j,\ 0^j1^k,\ 1^k$ のどの場合も $\vect{x}\vect{y}^2\vect{z}\not\in L$ であるから、反復補題に矛盾する。
正則言語の判定問題
有限オートマトン、正則文法、正規表現等で与えられた正則言語に関わる様々な判定問題が判定可能であることを示す。
定理．正則言語$L,L'\subseteq\Sigma^*$と語$\vect{w}\in\Sigma^*$に対し、次が成立つか否かを判定するアルゴリズムが存在する。
１．$L=\emptyset,\ L=\Sigma^*,\ L\subseteq L'$
２．$\vect{w}\in L$
証明．$L=\emptyset$か否かは$L$を認識するDFAに開始状態から受理状態へ至る路があるか否かで判定できる。以下、