この章の概要
正則言語の応用では、正規(正則)表現で与えられた正則言語に属する文字列を検索(認識)し、その文字列に対し、定義された置換やアクションを行う事例を扱った。それができるのは、正規表現をDFA(認識プログラム)に変換できるからである。本章では、CFGをPDAに変換できるという事実が、どのように応用されるかを見ていく。前章でも少し触れたが、CFGは、導出木を介して、生成文字列に対しその意味を解析する手がかりを与える。生成文字列に対しその導出木を求める作業を構文解析といい、本章では導出木を構文木と呼ぶ。前章でも述べたように、最左(右)導出は、構文木と1対1対応するから、構文木を求めることと最左(右)導出を求めることは本質的に同じである。
CFL(CFG)には必然的にあいまい性が伴い、決定性PDAは非決定性PDAより能力が低い。しかし、構文解析の観点からはマシーン(プログラム)は決定性である必要があるため、様々な工夫を必要とする。本章では、アイディアのみ紹介し、与えられた(非決定性)構文解析器が決定性であるための詳細については省略するが、詳しくは、構文解析の専門書を参考にして欲しい。
・プログラミング言語の記述への応用について学ぶ
・コンパイラコンパイラについて学ぶ
・XMLの記述への応用について学ぶ
CFGの応用
本節では、CFGの応用例として、HTMLプロセッサー(Webブラウザ)とプログラム言語のコンパイラを簡単に紹介しよう。これらはいわば、言語の文字列(Webページの記述やプログラム)を解釈・実行するオートマトンであるが、基本は、言語の骨格がCFGで記述される点にある。HTML
HTML(Hyper Text Markup Language)はWebページの記述言語であり、タグと呼ばれる<要素名>要素内容</要素名>の形をした括弧構造を持つ。ブラウザはタグ情報を解釈して要素内容をそれに適した形式で表示する。
| HTMLの例(リスト) | ブラウザによる表示 |
<ol><li>リストの第1項</li> <li>リストの第2項</li></ol> |
|
HTMLの文法はCFGで記述できる。以下はその一部で、斜体は非終端記号(文法要素)を表す。
Char → a | A |・・・ (文字)
Text → ε|Char Text (文字列)
Doc → ε|Element Doc (要素列)
Element → Text | <EM>Doc</EM> | <OL>List</OL> | ・・・ (要素)
List → ε| <LI>Doc</LI> List (OL要素:リスト)
プログラミング言語の記述
前の章ではCFGの例として挙げた簡単な数式に限らず、プログラミング言語(の骨格)はあいまいでないCFGで記述できる。実際、プログラミング言語は多くの括弧構造を持ち、RGでは記述できない。
C,Java:( ), [ ], { }, /* */, if else
Pascal:( ), [ ], begin end, { }
簡単な例題として、iC, Java におけるif elseは緩やかな括弧構造ではelseを伴わないifも許され、例えば以下のように記述できる。
$S \to $if ($C$) $S$ else $S$ | if ($C$) $S$
パズル.上記の文法はあいまいで
if ($C$) if ($C$) $S$ else $S$
は複数の構文木(解釈)を持つ。それを示せ。
elseが直前のifと対をなすことを反映した曖昧でない文法は次の通り。
$S \to$ if ($C$) $S_{ie}$ else $S$ | if ($C$) $S$ | …(その他の規則)
$S_{ie} \to$ if ($C$) $S_{ie}$ else $S$ | …(その他の規則)
構文解析
以下、文脈自由文法を$G{=}(\Gamma,\Sigma,P,S)$とする。$\vect{w}\in\Sigma^*$の構文解析には、2つの考え方があり、$\vect{w}$を左から右に読みながら、1. $\vect{w}$の最左導出、即ち構文木を上から下へ(Top Down)構成する
2. $\vect{w}$の最右導出の逆順、即ち構文木を下から上へ(Bottom Up)構成する
導出の逆を還元という。(最右)導出$S\overset{*}{\Rightarrow}\vect{w}$の逆順は$\vect{w}$から$S$への(最左)還元列である。
例.$G:E\to E{+}E\mid E{*}E\mid(E)\mid a\mid b$での $a{+}b{*}a$ の導出例を考える。
最左導出:$S\Rightarrow E{+}E\Rightarrow a{+}E\Rightarrow a{+}E{*}E\Rightarrow a{+}b{*}E\Rightarrow a{+}b{*}a$
最右導出の逆順:$a{+}b{*}a\Leftarrow E{+}b{*}a\Leftarrow E{+}E{*}a\Leftarrow E{+}E{*}E\Leftarrow E{+}E\Leftarrow E$
問.例に示した導出(の逆)順にしたがって各々構文木を構成せよ。
LL構文解析
前章でCFG$\,G{=}(\Gamma,\Sigma,P,S)$から構成した$\varepsilon$受理PDA$M{=}(\{q\},\Sigma,\Sigma\dot\cup\Gamma,\delta_c\dot\cup\delta_d,q,S,\emptyset),$
$\delta_c{=}\{(q,a,a;\varepsilon,q)\mid a\in\Sigma\},\ \delta_d{=}\{(q,\varepsilon,A;\alpha,q)\mid A\to\alpha \in P\}$ は、
例.$G:E\to E{+}E\mid E{*}E\mid(E)\mid a\mid b$での $a{+}b{*}a$ のLL構文解析を考える。
状態$q$は省略すると、以下の$\delta_d$の動作順(赤と茶色)は各々最左導出を与える。
- $E]a{+}b{*}a \textcolor{red}{\boldsymbol\vdash} E{+}E]a{+}b{*}a \textcolor{red}{\boldsymbol\vdash} a{+}E]a{+}b{*}a \vdash {+}E]{+}b{*}a \vdash E]b{*}a\\ \textcolor{red}{\boldsymbol\vdash} E{*}E]b{*}a \textcolor{red}{\boldsymbol\vdash} b{*}E]b{*}a \vdash {*}E]{*}a \vdash E]a \textcolor{red}{\boldsymbol\vdash} a]a \vdash {]}$
- $E]a{+}b{*}a \textcolor{brown}{\boldsymbol\vdash} E{*}E]a{+}b{*}a \textcolor{brown}{\boldsymbol\vdash} E{+}E{*}E]a{+}b{*}a \textcolor{brown}{\boldsymbol\vdash}a{+}E{*}E]a{+}b{*}a\\ \vdash {+}E{*}E]{+}b{*}a \vdash E{*}E]b{*}a \textcolor{brown}{\boldsymbol\vdash} b{*}E]b{*}a \vdash {*}E]{*}a \vdash E]a \textcolor{brown}{\boldsymbol\vdash} a]a \vdash {]}$
上で述べたPDAは非決定的な$\delta_d$動作を含むから、その対処が必要である。特に応用上重要なのは$\delta_d$動作を決定的に選択する仕組みで、入力の$k$文字の先読み機能を付け加えることで動作が決定できる文法をLL($k$)文法といい、先読みDFAを付け加えて動作が決定できる文法をLL(*)文法という。文脈自由言語は本質的にあいまいだから、これらの文法は生成言語の制限になっているが。応用上重要な文法として広く研究されている。詳細は構文解析の教科書等を参照して欲しい。
再帰下降法
規則$A\to X_1X_2\cdots X_k$に対し$A$を根とする構文木(最左導出)の構成は、それぞれ$X_1,\ X_2,\dots,\ X_k$を根とする構文木(最左導出)の(この順の)構成に分解できる。
各$a\in\Sigma^?$に対し関数$a(x)$を以下で定義する
$a(x):=\begin{cases} \vect{v} & \dlarrow x=a\vect{v}\\ 失敗 & それ以外 \end{cases}$
各$A\in\Gamma$に対し関数$A(x)$を、右表の$\sqcup$を用いて以下で定義する。
$A(x):=\begin{cases} 失敗 & \dlarrow x=失敗\\ \displaystyle\bigsqcup_{A\to X_1X_2\cdots X_k\in P} X_k(\cdots X_2(X_1(x))\cdots) & それ以外 \end{cases}$
$X\in \Sigma^?\dot\cup\Gamma$に対し、$X(\vect{w})=\varepsilon \drarrow X\overset{*}{\Rightarrow}\vect{w}\wedge X(\vect{w}\vect{v})=\vect{v}$が成立ち、
$G(x):=\displaystyle\bigvee_{S\to X_1X_2\cdots X_k\in P} X_k(\cdots X_2(X_1(x))\cdots)=\varepsilon$
とおけば、$G(\vect{w})=真 \drarrow \vect{w}\in \mathcal{L}(G)$である。
例.$G:E\to a\mid b\mid E{+}E\mid E{*}E\mid(E)$での $a{+}b{*}a$を考える。上の定義で、規則をこの順に試すと、真(成功)に至る以下の道筋から最左導出(構文木)を得る。
$G(a+b*a):{}^①E(+(E(a+b*a)))=E(+(a(a+b*a)))=E(+(+b*a))\\
=E(b*a)=E(*(E(b*a)))=E(*(b(b*a)))=E(*(*a))=E(a)=a(a)=\varepsilon$
① $a(a+b*a)=+b*a\ne\varepsilon,\ b(a+b*a)=失敗$より。以下同様。
問.1.$G:E\to a\mid E{-}E$での$G(a{-}a{-}a)$の計算で得られる構文木は適切か。
2. 規則の順序を$G:E\to E{-}E\mid a$とした場合$G(a{-}a{-}a)$の計算はどうなるか
問にも見られるように、この定義(手法)には以下のような問題がある
問.$G:\begin{cases} E \to T \mid E+T \mid E-T\\ T \to F \mid T*F \mid T/F\\ F \to a \mid b \mid (E) \end{cases}$ に対し、上で述べた再帰下降法は適切な構文木を与えることをいくつかの例で確認せよ。
注.$E,T$に対し各々規則$E\to T,\ T\to F$を最初に試すので計算は循環しないが、バックトラックを含むので効率は悪い。
規則$A\to X_1X_2\cdots X_k$に対し$A$を根とする構文木(最左導出)の構成は、それぞれ$X_1,\ X_2,\dots,\ X_k$を根とする構文木(最左導出)の(この順の)構成に分解できる。
| $x_1\backslash x_2$ | $\vect{w}_2$ | 失敗 |
| $\vect{w}_1$ | $\vect{w}_1$ | $\vect{w}_1$ |
| 失敗 | $\vect{w}_2$ | 失敗 |
$a(x):=\begin{cases} \vect{v} & \dlarrow x=a\vect{v}\\ 失敗 & それ以外 \end{cases}$
各$A\in\Gamma$に対し関数$A(x)$を、右表の$\sqcup$を用いて以下で定義する。
$A(x):=\begin{cases} 失敗 & \dlarrow x=失敗\\ \displaystyle\bigsqcup_{A\to X_1X_2\cdots X_k\in P} X_k(\cdots X_2(X_1(x))\cdots) & それ以外 \end{cases}$
$X\in \Sigma^?\dot\cup\Gamma$に対し、$X(\vect{w})=\varepsilon \drarrow X\overset{*}{\Rightarrow}\vect{w}\wedge X(\vect{w}\vect{v})=\vect{v}$が成立ち、
$G(x):=\displaystyle\bigvee_{S\to X_1X_2\cdots X_k\in P} X_k(\cdots X_2(X_1(x))\cdots)=\varepsilon$
とおけば、$G(\vect{w})=真 \drarrow \vect{w}\in \mathcal{L}(G)$である。
例.$G:E\to a\mid b\mid E{+}E\mid E{*}E\mid(E)$での $a{+}b{*}a$を考える。上の定義で、規則をこの順に試すと、真(成功)に至る以下の道筋から最左導出(構文木)を得る。
問.1.$G:E\to a\mid E{-}E$での$G(a{-}a{-}a)$の計算で得られる構文木は適切か。
2. 規則の順序を$G:E\to E{-}E\mid a$とした場合$G(a{-}a{-}a)$の計算はどうなるか
問にも見られるように、この定義(手法)には以下のような問題がある
- 失敗の際は戻って他の規則を試すバックトラックを含み一般に効率が悪い
- $A\overset{*}{\Rightarrow}A\alpha$となるとき、$A$の定義(計算)が循環する場合がある
- 文法が曖昧な場合、上の定義で求まる最左導出が適切とは限らない
- 計算の際の規則$A\to X_1X_2\cdots X_k\in P$の適用順序で求まる構文木が異なる
問.$G:\begin{cases} E \to T \mid E+T \mid E-T\\ T \to F \mid T*F \mid T/F\\ F \to a \mid b \mid (E) \end{cases}$ に対し、上で述べた再帰下降法は適切な構文木を与えることをいくつかの例で確認せよ。
注.$E,T$に対し各々規則$E\to T,\ T\to F$を最初に試すので計算は循環しないが、バックトラックを含むので効率は悪い。
Earley法
文法を制限せず。ダイナミックプログラミングの手法により構文木(最左導出)をすべて求めるEarley法を紹介しよう。与えられたCFG$\,G=(\Gamma,\Sigma,P,S)$と語$\vect{w}=a_0a_1\cdots a_{n-1}\in\Sigma^*$に対し、Earley法では・付き規則$A{\to}\alpha\cdot\beta,\ A{\to}\alpha\beta{\in}P$の集合の表$S(j,k),\ 0{\le}j{\le}k{\le}n$を構成する。ここで、$A{\to}\alpha\cdot\beta\in S(j,k)$は、$\vect{w}$の部分語$a_j\cdots a_{k-1}$や$\varepsilon\ (j{=}k)$が規則$A\to\alpha\beta$の$\alpha$から生成されうることを意味する。
Earley法のアルゴリズムは次の【基礎】から始め、
【基礎】$S{\to}\alpha \in P \drarrow S{\to}\cdot\alpha\in S(0,0)$
・の左が$\to,\Sigma,\Gamma$かに対応した次の操作を各$S(j,k)$が増えなくなるまで繰り返す。
【予測${\to}\cdot$】$X{\to}\alpha\cdot Y\beta\in S(j,k)\wedge Y{\to}\gamma \in P \drarrow Y{\to}\cdot\gamma\in S(k,k)$
【走査$\Sigma\cdot$】$X{\to}\alpha\cdot a_k\beta\in S(j,k)\drarrow X{\to}\alpha a_k\cdot\beta\in S(j,k{+}1)$
【完了$\Gamma\cdot$】$X{\to}\alpha\cdot Y\beta\in S(i,j)\wedge Y{\to}\gamma\cdot{}\in S(j,k) \drarrow X{\to}\alpha Y\cdot\beta\in S(i,k)$
最終的に、$S{\to}\alpha\cdot{}\in S(0,n)\darrow{\rightarrow}{\leftarrow}\vect{w}\in \mathcal{L}(G)$であり、その構成過程(【完了】の適用)を追跡すれば$\vect{w}$の構文木が得られる。
例.$G:E\to E{+}E\mid E{*}E\mid(E)\mid a\mid b$での $a{+}b{*}a$ を考える。Earley法では
$S(0,0)=\{E\to \cdot E+E\mid \cdot E*E\mid \cdot (E) \mid \cdot a \mid \cdot b\}$
$a_1=a:\ S(0,1)=\{E\to a\cdot \mid E\cdot +E\mid E\cdot *E\},\ S(1,1)=\emptyset$
$a_2={+}:\ S(0,2)=\{E\to E+\cdot E\},\ S(1,2)=\emptyset,$
$S(2,2)=\{E\to \cdot E+E\mid \cdot E*E\mid \cdot (E) \mid \cdot a \mid \cdot b\}$
$a_3=b:\ S(0,3)=\{E\to E+E\cdot \mid E\cdot +E\mid E\cdot *E\},\ S(1,3)=\emptyset,$
$S(2,3)=\{E\to b\cdot\mid E\cdot +E\mid E\cdot *E\},\ S(3,3)=\emptyset$
$a_4={*}:\ S(0,4)=\{E\to E*\cdot E\},\ S(1,4)=\emptyset,\ S(2,4)=\{E\to E*\cdot E\},$
$S(3,4)=\emptyset,\ S(4,4)=\{E\to \cdot E+E\mid \cdot E*E\mid \cdot (E) \mid \cdot a \mid \cdot b \}$
$a_5=a:\ S(0,5)=\{E\to E*E\cdot \mid E\cdot +E\mid E\cdot *E \mid E+E\cdot \}$
$S(1,5)=\emptyset,\ S(2,5)=\{E\to E*E\cdot \mid E\cdot +E \mid E\cdot *E \},$
$S(3,5)=\emptyset,\ S(4,5)=\{E\to a\cdot \mid E\cdot +E\mid E\cdot *E\},\ S(5,5)=\emptyset$
となり、$S(0,5)$に1.$E\to E+E\cdot$、2.$E\to E*E\cdot$の2導出が示されている。
以下、各導出に関わる・付き規則を、予測、完了での$j$の値を付けて示す。
1. $S(0,0)=\{E\to \cdot E+E\mid \cdot a \}$
$a_1{=}a:\ S(0,1){=}\{E\to a\cdot \mid E\cdot +E;0\}$
$a_2{=}{+}:\ S(0,2){=}\{E\to \textcolor{red}{E+\cdot E}\},\ S(2,2){=}\{E\to \cdot E*E;0\mid \cdot b;0\}$
$a_3{=}b:\ S(2,3){=}\{E\to b\cdot\mid E\cdot *E;2 \}$
$a_4{=}{*}:\ S(2,4){=}\{E\to E*\cdot E \},\ S(4,4){=}\{E\to \cdot a;2 \},$
$a_5{=}a:\ S(4,5){=}\{E\to a\cdot\},\ S(2,5){=}\{E\to \textcolor{red}{E*E\cdot};4\},\ S(0,5){=}\{E\to \textcolor{red}{E+E\cdot;2} \}$
2. $S(0,0)=\{E\to \cdot E+E\mid \textcolor{brown}{\cdot E*E} \mid \cdot a \}$
$a_1{=}a:\ S(0,1){=}\{E\to a\cdot \mid E\cdot +E;0\}$
$a_2{=}{+}:\ S(0,2){=}\{E\to E+\cdot E\},\ S(2,2){=}\{E\to \cdot b;2\}$
$a_3{=}b:\ S(2,3){=}\{E\to b\cdot \},\ S(0,3){=}\{E\to \textcolor{brown}{E+E\cdot};2 \mid \textcolor{brown}{E\cdot *E;0}\}$
$a_4{=}{*}:\ S(0,4){=}\{E\to E*\cdot E\},\ S(4,4){=}\{E\to \cdot a;0 \}$
$a_5{=}a:\ S(4,5){=}\{E\to a\cdot\},\ S(0,5){=}\{E\to E*E\cdot;4 \}$
問.上の例から、各々の最左導出(導出木)を構成せよ。
ヒント:ポイントなる箇所を赤・茶色で示した。
文法を制限せず。ダイナミックプログラミングの手法により構文木(最左導出)をすべて求めるEarley法を紹介しよう。与えられたCFG$\,G=(\Gamma,\Sigma,P,S)$と語$\vect{w}=a_0a_1\cdots a_{n-1}\in\Sigma^*$に対し、Earley法では・付き規則$A{\to}\alpha\cdot\beta,\ A{\to}\alpha\beta{\in}P$の集合の表$S(j,k),\ 0{\le}j{\le}k{\le}n$を構成する。ここで、$A{\to}\alpha\cdot\beta\in S(j,k)$は、$\vect{w}$の部分語$a_j\cdots a_{k-1}$や$\varepsilon\ (j{=}k)$が規則$A\to\alpha\beta$の$\alpha$から生成されうることを意味する。
Earley法のアルゴリズムは次の【基礎】から始め、
【基礎】$S{\to}\alpha \in P \drarrow S{\to}\cdot\alpha\in S(0,0)$
・の左が$\to,\Sigma,\Gamma$かに対応した次の操作を各$S(j,k)$が増えなくなるまで繰り返す。
【予測${\to}\cdot$】$X{\to}\alpha\cdot Y\beta\in S(j,k)\wedge Y{\to}\gamma \in P \drarrow Y{\to}\cdot\gamma\in S(k,k)$
【走査$\Sigma\cdot$】$X{\to}\alpha\cdot a_k\beta\in S(j,k)\drarrow X{\to}\alpha a_k\cdot\beta\in S(j,k{+}1)$
【完了$\Gamma\cdot$】$X{\to}\alpha\cdot Y\beta\in S(i,j)\wedge Y{\to}\gamma\cdot{}\in S(j,k) \drarrow X{\to}\alpha Y\cdot\beta\in S(i,k)$
最終的に、$S{\to}\alpha\cdot{}\in S(0,n)\darrow{\rightarrow}{\leftarrow}\vect{w}\in \mathcal{L}(G)$であり、その構成過程(【完了】の適用)を追跡すれば$\vect{w}$の構文木が得られる。
例.$G:E\to E{+}E\mid E{*}E\mid(E)\mid a\mid b$での $a{+}b{*}a$ を考える。Earley法では
$S(0,0)=\{E\to \cdot E+E\mid \cdot E*E\mid \cdot (E) \mid \cdot a \mid \cdot b\}$
$a_1=a:\ S(0,1)=\{E\to a\cdot \mid E\cdot +E\mid E\cdot *E\},\ S(1,1)=\emptyset$
$a_2={+}:\ S(0,2)=\{E\to E+\cdot E\},\ S(1,2)=\emptyset,$
$S(2,2)=\{E\to \cdot E+E\mid \cdot E*E\mid \cdot (E) \mid \cdot a \mid \cdot b\}$
$a_3=b:\ S(0,3)=\{E\to E+E\cdot \mid E\cdot +E\mid E\cdot *E\},\ S(1,3)=\emptyset,$
$S(2,3)=\{E\to b\cdot\mid E\cdot +E\mid E\cdot *E\},\ S(3,3)=\emptyset$
$a_4={*}:\ S(0,4)=\{E\to E*\cdot E\},\ S(1,4)=\emptyset,\ S(2,4)=\{E\to E*\cdot E\},$
$S(3,4)=\emptyset,\ S(4,4)=\{E\to \cdot E+E\mid \cdot E*E\mid \cdot (E) \mid \cdot a \mid \cdot b \}$
$a_5=a:\ S(0,5)=\{E\to E*E\cdot \mid E\cdot +E\mid E\cdot *E \mid E+E\cdot \}$
$S(1,5)=\emptyset,\ S(2,5)=\{E\to E*E\cdot \mid E\cdot +E \mid E\cdot *E \},$
$S(3,5)=\emptyset,\ S(4,5)=\{E\to a\cdot \mid E\cdot +E\mid E\cdot *E\},\ S(5,5)=\emptyset$
となり、$S(0,5)$に1.$E\to E+E\cdot$、2.$E\to E*E\cdot$の2導出が示されている。
以下、各導出に関わる・付き規則を、予測、完了での$j$の値を付けて示す。
1. $S(0,0)=\{E\to \cdot E+E\mid \cdot a \}$
$a_1{=}a:\ S(0,1){=}\{E\to a\cdot \mid E\cdot +E;0\}$
$a_2{=}{+}:\ S(0,2){=}\{E\to \textcolor{red}{E+\cdot E}\},\ S(2,2){=}\{E\to \cdot E*E;0\mid \cdot b;0\}$
$a_3{=}b:\ S(2,3){=}\{E\to b\cdot\mid E\cdot *E;2 \}$
$a_4{=}{*}:\ S(2,4){=}\{E\to E*\cdot E \},\ S(4,4){=}\{E\to \cdot a;2 \},$
$a_5{=}a:\ S(4,5){=}\{E\to a\cdot\},\ S(2,5){=}\{E\to \textcolor{red}{E*E\cdot};4\},\ S(0,5){=}\{E\to \textcolor{red}{E+E\cdot;2} \}$
2. $S(0,0)=\{E\to \cdot E+E\mid \textcolor{brown}{\cdot E*E} \mid \cdot a \}$
$a_1{=}a:\ S(0,1){=}\{E\to a\cdot \mid E\cdot +E;0\}$
$a_2{=}{+}:\ S(0,2){=}\{E\to E+\cdot E\},\ S(2,2){=}\{E\to \cdot b;2\}$
$a_3{=}b:\ S(2,3){=}\{E\to b\cdot \},\ S(0,3){=}\{E\to \textcolor{brown}{E+E\cdot};2 \mid \textcolor{brown}{E\cdot *E;0}\}$
$a_4{=}{*}:\ S(0,4){=}\{E\to E*\cdot E\},\ S(4,4){=}\{E\to \cdot a;0 \}$
$a_5{=}a:\ S(4,5){=}\{E\to a\cdot\},\ S(0,5){=}\{E\to E*E\cdot;4 \}$
問.上の例から、各々の最左導出(導出木)を構成せよ。
ヒント:ポイントなる箇所を赤・茶色で示した。
LR構文解析
入力を左から右に読み(Left to right)、最右導出(Right-most derivation)の逆順(最左還元)を構成するLR構文解析器の動作を理解するためには、時点表示$\alpha]q\vect{w}$のスタックを逆順にして$q\vect{w}\{\alpha^R$と表すと都合がよい。即ち、条件$Z]q\vect{w} \VDASH{}{*} \beta^R Z]q \darrow{\rightarrow}{\leftarrow}q\vect{w}\{Z \VDASH{}{*} q\{Z\beta \darrow{\rightarrow}{\leftarrow}{}$最右導出で$\beta\overset{*}{\Rightarrow}\vect{w}$
を満たす$\varepsilon$受理(拡張)PDA$M{:=}(\{q\},\Sigma,\Sigma\dot\cup\Gamma\dot\cup\{Z\},\delta_s\dot\cup\delta_r\dot\cup\{(q,\varepsilon,SZ;\varepsilon,q)\},q,Z,\emptyset)$を、$\delta_s{:=}\{(q,a,\varepsilon;a,q)\mid a\in \Sigma\},\
\delta_r{:=}\{(q,\varepsilon,\alpha^R;A,q)\mid A\to\alpha\in P\}$と定義する。ここで$\delta_r$の動作は還元と呼ばれ、スタック上部にある(長さ$1$以上の)記号列$\alpha^R$をまとめて$A$に置き換えるという(本質的ではない)拡張機能である。【還元動作はPDAの複数の動作に分解できる】
$\begin{cases}
(q,a,\varepsilon;a,q)\in \delta_s & \darrow{\rightarrow}{\leftarrow}
\alpha^R]qa\vect{w} \vdash a\alpha^A]q\vect{w} & \darrow{\rightarrow}{\leftarrow}
qa\vect{w}\{\alpha \vdash q\vect{w}\{\alpha a\\
(q,\varepsilon,\alpha^R;A,q)\in \delta_r & \darrow{\rightarrow}{\leftarrow}
\alpha^R\beta^R]q\vect{w} \vdash A\beta^R]q\vect{w} & \darrow{\rightarrow}{\leftarrow}
q\vect{w}\{\beta\alpha \vdash q\vect{w}\{\beta A
\end{cases}$
だから、CFG$G$の最右導出と$M$の動作列との間には、次の関係が成立つ。
$\begin{cases}
\beta a\overset{*}\Rightarrow \vect{w}a \darrow{\rightarrow}{\leftarrow} \beta \overset{*}\Rightarrow \vect{w} & \darrow{\rightarrow}{\leftarrow} q\vect{w}a\{Z \VDASH{}{*} qa\{Z\beta \vdash q\{Z\beta a\\
\beta A \Rightarrow \beta\alpha \overset{*}\Rightarrow \vect{w} & \darrow{\rightarrow}{\leftarrow} q\vect{w}\{Z \VDASH{}{*} q\{Z\beta\alpha \vdash q\{Z\beta A \end{cases}$
よって $q\vect{w}\{Z \VDASH{}{*} q\{ZS \vdash q{[} \darrow{\rightarrow}{\leftarrow} S\overset{*}{\Rightarrow}\vect{w}$ が成立ち、$\vect{w}$の受理動作列から$\delta_r$の動作を取り出せば、$S\overset{*}\Rightarrow\vect{w}$の最右導出の逆順が得られる。
$\delta_s$の動作をシフトと言い、このタイプのPDAをシフト還元機械という。
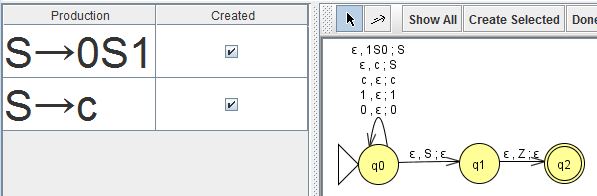 例.JFLAPによるCFGのシフト還元機械(PDA(LR))への変換とその動作例。
例.JFLAPによるCFGのシフト還元機械(PDA(LR))への変換とその動作例。
(スタック$SZ]$の処理はテキストと異なる)
$Z]q_00c1 \vdash 0Z]q_0c1 \vdash c0Z]q_01 \vdash S0Z]q_01 \vdash 1S0Z]q_0 \vdash SZ]q_0 \VDASH{}{*} {]}q_2$
($q_00c1\{Z \vdash q_0c1\{Z0 \vdash q_01\{Z0c \vdash q_01\{Z0S \vdash q_0\{Z0S1 \vdash q_0\{ZS \VDASH{}{*} q_2\{$)
例.$G:E\to E{+}E\mid E{*}E\mid(E)\mid a\mid b$での $a{+}b{*}a$ のLR構文解析を考える。
状態$q$を省略した次の動作列中の$\delta_r$の動作の逆順は最右導出(構文木)を与える。1. $a{+}b{*}a\{Z \vdash {+}b{*}a\{Za \textcolor{red}{\boldsymbol\vdash}{+}b{*}a\{ZE \vdash b{*}a\{ZE{+} \vdash {*}a\{ZE{+}b \textcolor{red}{\boldsymbol\vdash} {*}a\{ZE{+}E\\
\vdash a\{ZE{+}E{*} \vdash \{ZE{+}E{*}a \textcolor{red}{\boldsymbol\vdash} \{ZE{+}E{*}E \textcolor{red}{\boldsymbol\vdash} \{ZE{+}E \textcolor{red}{\boldsymbol\vdash}\{ZE \vdash {\{}$
2. $a{+}b{*}a\{Z \vdash {+}b{*}a\{Za \textcolor{brown}{\boldsymbol\vdash} {+}b{*}a\{ZE \vdash b{*}a\{ZE{+} \vdash {*}a\{ZE{+}b \textcolor{brown}{\boldsymbol\vdash} {*}a\{ZE{+}E\\
\textcolor{brown}{\boldsymbol\vdash} {*}a\{ZE \vdash a\{ZE{*}\vdash \{ZE{*}a \textcolor{brown}{\boldsymbol\vdash} \{ZE{*}E \textcolor{brown}{\boldsymbol\vdash} \{ZE \vdash {\{}$
入力の$k$文字の先読み機能を付け加えることで動作が決定できる文法をLR($k$)文法といい、他にも様々な工夫が知られている。LR構文解析における遷移選択の仕組みは、規則右辺の情報が使えるので左辺から選ぶLL構文解析より簡単になる。そのため、以下に述べるコンパイラ・コンパイラ等に応用されている。
入力を左から右に読み(Left to right)、最右導出(Right-most derivation)の逆順(最左還元)を構成するLR構文解析器の動作を理解するためには、時点表示$\alpha]q\vect{w}$のスタックを逆順にして$q\vect{w}\{\alpha^R$と表すと都合がよい。即ち、条件
$\delta_s$の動作をシフトと言い、このタイプのPDAをシフト還元機械という。
(スタック$SZ]$の処理はテキストと異なる)
$Z]q_00c1 \vdash 0Z]q_0c1 \vdash c0Z]q_01 \vdash S0Z]q_01 \vdash 1S0Z]q_0 \vdash SZ]q_0 \VDASH{}{*} {]}q_2$
($q_00c1\{Z \vdash q_0c1\{Z0 \vdash q_01\{Z0c \vdash q_01\{Z0S \vdash q_0\{Z0S1 \vdash q_0\{ZS \VDASH{}{*} q_2\{$)
例.$G:E\to E{+}E\mid E{*}E\mid(E)\mid a\mid b$での $a{+}b{*}a$ のLR構文解析を考える。
状態$q$を省略した次の動作列中の$\delta_r$の動作の逆順は最右導出(構文木)を与える。
入力の$k$文字の先読み機能を付け加えることで動作が決定できる文法をLR($k$)文法といい、他にも様々な工夫が知られている。LR構文解析における遷移選択の仕組みは、規則右辺の情報が使えるので左辺から選ぶLL構文解析より簡単になる。そのため、以下に述べるコンパイラ・コンパイラ等に応用されている。
コンパイラコンパイラ
プログラム言語で書かれたプログラムを解釈し、コンピュータが実行可能な機械語に翻訳するコンパイラは、構文解析で紹介した手法を用いて構築される。lexでは正規表現とアクションの対で字句解析器が自動構築(記述)できたように、コンパイラコンパイラは、CFGの規則とアクションの対からLR構文解析に基づきコンパイラを自動構築する。YACC
YACC(Yet Another Compiler Compiler)は
- 言語の文法を与えるとその構文解析器(決定性シフト還元機械)を出力し
- 言語の文法+アクションを与えると、構文解析器が還元を行うたびに対応するアクションを実行するコンパイラーを出力する
$\$\$$は左辺の記号の値
$\$n$は右辺の$n$番目の記号の値
s : e '=' {$1を表示;}
e : '(' e ')' {$$=$2;}
| e '+' e {$$=$1+$3;}
| e '*' e {$$=$1*$3;}
| N {$$=$1;}
;
この記述が与えられると、YACCは加算と乗算と括弧からなる数式を計算する電卓を出力する。この電卓に例えば"2+3="と入力すると以下のように動作して"5"と表示する。動作例:値が$k$の式$e$を$e[k]$と表す。⇒は還元[アクション]動作
$2+3{=}\{{}⇒ +3{=}\{2$⇒$+3{=}\{e[2]⇒3{=}\{e[2]'+'⇒{=}\{e[2]'+'3$⇒${=}\{e[2]'+'e[3]$⇒${=}\{e[5]⇒ \{e[5]'='$⇒$\{S[5を表示]$
注.YACCには決定性シフト還元機械を生成するための様々な工夫がある。
XMLと文書型の定義
HTMLにはCSSといい、タグで指定された要素の表示をカスタマイズする機能がある。XMLではさらに進んで、利用者がタグを自由に定義し、定義された要素に対する表示形式や処理内容を設定できる。システム内で使うXML文書を生成する(拡張)CFGをDTD(標準型定義)という。以下の例はパソコン(PC)のデータベースの構造を規定するDTDとそれが生成するXML文書である。
| DTD | XML文書 |
<!DOCTYPE PcSpecs [ <!ELEMENT PCS (PC*)> <!ELEMENT PC (MODEL,PRICE,PROCESSOR, RAM,DISK+)> <!ELEMENT MODEL (\#PCDATA)> ・・・ ]> |
<PCS> <PC> <MODEL>PC2016</MODEL> <PRICE>15,000</PRICE> ・・・ </PC> <PC> <MODEL>NOTE16</MODEL> <PRICE>5,000</PRICE> ・・・ </PC> </PCS> |
DTDに基づいてXML文書の、
文脈自由言語の判定問題
正則言語とは異なり、文脈自由言語では多くの判定問題が判定不能であるが、まずは、判定可能な問題を見ていこう。定理.CFL$L\subseteq \Sigma^*, \vect{w}\in\Sigma^*$に対し、$L=\emptyset$か否か、$\vect{w}\in L$か否かは判定可能。
証明.$\vect{w}\in L$か否かはEarley法で判定できる。$L=\emptyset$か否かは、$L$の生成するCFG $G=(\Gamma,\Sigma,P,S)$において、集合$\Delta:=\{A\in\Gamma\mid \mathcal{L}(A,G)\ne\emptyset\}$の帰納的定義、1.$\Delta=\emptyset$, 2.$A{\to}\alpha \in P \wedge \alpha\in (\Sigma{\cup}\Delta)^* \drarrow A\in \Delta$によって判定できる。
| $i$ | $\vect{v}_i$ | $\vect{w}_i$ |
| 1 | 10 | 101 |
| 2 | 011 | 11 |
| 3 | 101 | 011 |
| $i$ | $\vect{v}_i$ | $\vect{w}_i$ |
| 1 | 1 | 111 |
| 2 | 10111 | 10 |
| 3 | 10 | 0 |
定理.PCPの解の存在を判定するアルゴリズムは存在しない。
証明は、計算可能性の講で述べる。
PCPに対し次の文脈自由言語を考える。 $L_1:=\{i_n\cdots i_2i_1\#\vect{v}_{i_1}\vect{v}_{i_2}\cdots \vect{v}_{i_n}\mid n\ge 1\},\ L_2:=\{i_n\cdots i_2i_1\#\vect{w}_{i_1}\vect{w}_{i_2}\cdots \vect{w}_{i_n}\mid n\ge 1\}$
$L_1,L_2\subseteq(\Sigma\cup\{1,2,\dots,k\})\dot\cup\{\#\}$を認識するDPDAがあるので、$L_1,L_2,L_1^\complement,L_2^\complement$はすべて(決定性)文脈自由言語である。
問.CFL$L_1$を認識するDPDAが存在することを示せ。
定理.CFL $L,L'\subseteq \Sigma^*$に対し、以下を判定するアルゴリズムは存在しない。
- $L\cap L'=\emptyset$か否か
- CFG $G$があいまいか否か
- $L=\Sigma^*$か否か
- $L=L'$か否か
- $L_1\cap L_2=\emptyset\darrow{\rightarrow}{\leftarrow}$PCPが解をもたない
-
CFG $G$を以下で定める。$G: S\to A\mid B$
$A\to 1A\vect{v}_1\mid 2A\vect{v}_2\mid\cdots\mid kA\vect{v}_k\mid 1\#\vect{v}_1\mid 2\#\vect{v}_2\mid\cdots\mid k\#\vect{v}_k\\
\ B\to 1B\vect{w}_1\mid 2B\vect{w}_2\mid\cdots\mid kB\vect{w}_k\mid 1\#\vect{w}_1\mid 2\#\vect{w}_2\mid\cdots\mid k\#\vect{w}_k$
$G$が曖昧 $\darrow{\rightarrow}{\leftarrow}$ PCPが解を持つ。 - $L_1^\complement\cup L_2^\complement=\Gamma^*\darrow{\rightarrow}{\leftarrow}$ PCPが解を持つ
- $\Gamma^*$はCFLなので、3.より明らか