この章の目標
| チューリング機械 コンピュータ | 計算的可算言語 計算的部分関数 | 計算的可判定言語 計算的全域関数 | |
| 再帰関数 | 部分$\mu$関数 部分$\mu$集合 | 全域$\mu$関数 全域$\mu$集合 | 原始再帰関数 原始再帰集合 |
| 論理式 | $\Sigma_1$式 $\Sigma_1$集合 | $\Delta_1$式 $\Delta_1$集合 | $\Delta_0$式 $\Delta_0$集合 |
・プログラムの停止問題が計算不能であることを理解する
・ライスの定理について学ぶ
チューリング機械とコンピュータ
決定性チューリング機械(DTM)はコンピュータの数学的モデルであり、両者の計算能力は等しいと考えられる。まず歴史をおさらいしておこう。歴史
1936年：チューリングがチューリング機械を提唱（万能TMも）
映画「イミテーションゲーム」
1945年：ノイマンがプログラム内蔵方式（ノイマン型コンピュータ）を提唱
1946年：最初のコンピュータENIAC
1949年：最初の実用的ノイマン型コンピュータEDSAC
パズル．ENIACの写真とEDSACの写真に見られる大きな違いとその理由は何か
プログラム内臓方式のコンピュータは、メモリ中におかれたプログラムを読みながらその指示通りに動作するプログラム実行機械で、万能チューリング機械のアイディアをコンピュータ上で実現したものである。当初の機械の配線を変えてプログラムを実現する方式に比べ、各段にプログラム作成が容易になった。
コンピュータによるDTMの模倣
TMはDTMで模倣でき(前節の結果)、DTMを模倣するコンピュータプログラムは、例えばTMシミュレータ（作者のページ）にある。TMシミュレータはDTM(遷移)の記述と入力に対し、その動作を模倣するから、万能TMの実装である。ただ、TMのテープはいくらでも延長できるのに対し、コンピュータのメモリは(ハードディスクを含めても)有限である。しかし、外部記憶装置は必要に応じていくらでも増やせ、いくらでも大きなメモリー番地を利用できると仮定して(すれば)よい。本節で考えるコンピュータには、この仮定を置く。
DTMによるコンピュータの模倣コンピュータをDTMで模倣できることを示すために、まずコンピュータとは何かをできるだけ実態に即した形で定めておこう。コンピュータは右図のような構造を持ち、メモリは番地で管理され、通常は一定サイズ(例えば0,1の32桁)の区画に分かれているが、ここでは(いくらでも大きな番地を扱う必要から)そのサイズに制限はないと仮定する。右図CPU(中央演算処理装置)内のレジスタやカウンタ等も同様である。
コンピュータは基本動作サイクルで以下を繰返す。
- 命令カウンタの値(番地)を読み取る
- その番地にある命令を命令レジスタに移す
- プログラムカウンタの値を１増やす
- 命令デコーダが命令レジスタの命令を解釈し
- 汎用レジスタ(GR)や演算回路等を使って命令を実行する
コンピュータをシミュレートする(多テープ・万能)DTM$M$を構成しよう。$M$は有限制御部記憶と5本のテープを持ち、各々コンピュータの次のデータを保持する。- 有限制御部記憶：命令(番地部を除く)
- 記憶テープ：メモリー(番地と内容)
- 命令カウンタテープ：命令カウンタ
- 記憶番地テープ：命令中の番地部
- 入力ファイルテープ：コンピュータ入力
- メモテープ：汎用レジスタ・作業データ
$M$が指定された番地にアクセスするには、記憶テープ左端(の$\$$)にヘッドを移したのち、右に動きながら$\#$と$*$の間の0,1列が指定された(命令カウンタテープやメモテープ(GR)の)内容と一致する場所を探す。コンピュータの基本命令のうち、基本演算以外は(テープ間の)データコピーであるから、$M$で模倣できる。基本演算(演算回路による計算)は、出力付き有限オートマトン(ミーリ機械)で2進和を実現できたように、有限制御部で模倣できる。
前章で示したように、TM(NTM)とDTMの言語認識能力は等しいから、コンピュータとTMの言語認識能力は等しい。計算能力という意味では、TM$M{=}(\Sigma,\Gamma,\delta,q_0,F)$が計算するのは、決定性なら関数($:\Sigma^*{\to}\Gamma^*$)だが、非決定性なら関係(${\subseteq}\Sigma^*{\times}\Gamma^*$)になり、注意が必要である。本章ではTMはDTMであると仮定する。
部分再帰関数とDTM
本節では、計算のモデルを自然数上の部分関数の観点から論じる。部分再帰関数
$x_{1..n}$で列$x_1,x_2,\dots,x_n$を表し、$f(x_{1..n})$が$\mathbb{N}^n$から$\mathbb{N}$への部分関数であることを$f(x_{1..n}):\mathbb{N}^n\rightsquigarrow\mathbb{N}$と表す。 自然数$\mathbb{N}$上の部分再帰($\mathcal{P}\mu$)関数は再帰的に以下で定義され、とくにそれが全域関数であるとき全域再帰($\mathcal{T}\mu$)関数という。またそれらが$n$変数関数であるとき、$\mathcal{P}\mu_n,$ $\mathcal{T}\mu_n$と表す。
- 0、次者関数$s:x\mapsto x{+}1$、射影関数$p_{n,i}:x_{1..n}\mapsto x_i$は$\mathcal{T}\mu$である
- (関数合成)$f$が$\mathcal{P}\mu_m$、$g_{1..m}$が$\mathcal{P}\mu_n$なら、$f(g_{1..m}):x_{1..n}\mapsto f(g_1(x_{1..n}),\dots,g_m(x_{1..n}))$も$\mathcal{P}\mu_n$である。
-
(原始再帰)$g$が$\mathcal{P}\mu_n$、$h$が$\mathcal{P}\mu_{n+2}$なら、次で定義される$[g;h]$は$\mathcal{P}\mu_{n+1}$である。
$[g;h]:\begin{cases} (x_{1..n},0)\mapsto g(x_{1..n})\\ (x_{1..n},sx)\mapsto h(x_{1..n},x,[g;h](x_{1..n},x)) \end{cases}$ -
(最小化)$\mu_xp(x)$は、条件$p(x)$を満たす最小の$x$とし、そのような$x$が無ければ未定義とする。$f$が$\mathcal{P}\mu_{n+1}$なら、次で定義される$[\mu f]$は$\mathcal{P}\mu_n$である。
$[\mu f]:x_{1..n}\mapsto \mu_x(f(x_{1..n},x){\gt}0\wedge \forall y{\lt}x.f(x_{1..n},y){=}0)$
例1．以下は$\mathcal{PR}$である。$n{:=}s^n(0),$ $x\dot{-}1{:=}[0;p_{2,1}](x),$ $x_1{+}x{:=}[p_{1,1};s(p_{3,3})](x_1,x),$ $x_1\dot{-}x{:=}[p_{1,1};[0;p_{2,1}](p_{3,3})](x_1,x),$ $x_1{\times}x{:=}[0;[p_{1,1};s(p_{3,3})](p_{3,1},p_{3,3})](x_1,x)$
原始再帰の定義を具体的に書けば、$0\dot{-}1{=}0,$ $(x{+}1)\dot{-}1{=}p_{2,1}(x,x\dot{-}1){=}x,$ $x_1{+}0{=}p_{1,1}(x_1){=}x_1,$ $x_1{+}(x{+}1){=}s(p_{3,3}(x_1,x,(x_1{+}x))){=}(x_1{+}x){+}1$となる。以後簡単に、$x\dot{-}1{:=}[0;x{-}1],$ $x_1{+}x{:=}[x_1;(x_1{+}(x{-}1)){+}1]$のように表す。
問．1. $x_1\dot{-}x,$ $x_1{\times}x$の原始再帰の定義を具体的に書け。
2. $x_1^x,$ $x!$ が$\mathcal{PR}$であることを示せ。
次の定理(有界最小化)は$\mathcal{PR}$の能力を示す。
定理．$f$が$\mathcal{PR}_{n+1}$なら$[\mu_\le f]:(x_{1..n},x)\mapsto \mu_y(x{\lt}y\vee f(x_{1..n},y){\gt}0)$は$\mathcal{PR}_{n+1}$。
証明．$f,\ [\mu_\le f]$は共に全域関数で、$x{\lt}[\mu_\le f](a_{1..n},a)$なら$f(a_{1..n},x){=}0$である。
問．$[\mu_\le f](x_{1..n},x)=\sum_{z=0}^x\prod_{y=0}^z(1\dot{-}f(x_{1..n},y))$を示せ。
例2．$x_1{\div}x_2{:=}[\mu_\le(x_2{\times}(x{+}1)\dot{-}x_1)](x_{1..2},x_1),$ ※$x_1{\div}0=x_1{+}1$
$x_1 \bmod x_2{:=}x_1\dot{-}(x_1{\div}x_2){\times}x_2$ ※$x_1\bmod 0=x_1$
Ackermann関数 は
$A(m,n):=\begin{cases}
n{+}1 & \dlarrow m{=}0\\
A(m{-}1,1) & \dlarrow n{=}0\\
A(m{-}1,A(m,n{-}1)) & それ以外
\end{cases}$
で定義される。原始再帰はこの形を許しておらず、$\mathcal{PR}$でない$\mathcal{T}\mu$として知られる。実際、$f_
m(n){:=}A(m,n)$に対し上の定義式は
$f_0(n)=n{+}1,$ $f_m(n)=f_{m-1}^{n+1}(1)$と書け、$A(m,n)$の計算には概ね$m$重の原始再帰が必要になる。
問．Ackerman関数は全域関数であることを示せ。
ヒント．$m$に関する帰納法の中で$n$に関する帰納法を用いる。
DTMとの同等性
定理．$\mathcal{P}\mu$の計算能力はDTMと、$\mathcal{T}\mu$の計算能力は全入力で停止するDTMと等しい。
証明．$\mathcal{P}\mu$が、自然数を0,1で2進表示しいくらでも大きな数を扱えるとしたコンピュータで計算可能であることは、明らかだろう。実際、原始再帰や最小化の計算手順は右上のように書ける。よって前節の議論から$\mathcal{P}\mu$はDTMでも計算可能である。
逆は、一般性を失わずにDTM $M=(\{q_{0..r}\},\Sigma,\Gamma,\delta,q_0,\{q_r\}),$ $\Gamma{=}\{X_{0..p-1}\},$ $X_0{=}□$ とし、$\xi:\Gamma^*{\to}\mathbb{N}$を$\xi(\varepsilon){:=}0,\ \xi(X_j\alpha){:=}j{+}p{\times}\xi(\alpha),\ \alpha{\in}\Gamma^*$で定義すれば、$\xi(\alpha)=\xi(X_j\alpha){\div}p,$ $j=\xi(X_j\alpha)\bmod p$ だから、記号列左端での記号の取出し・追加は$\mathcal{PR}$で実現できる。※$\alpha^R$は$\xi(\alpha)$の$p$進表示で、$\xi(\alpha□^*) {=}\xi(\alpha)$が成立つ。
$M$の時点表示$\alpha q_i\beta$を自然数$\Xi(\alpha q_i\beta)=\| \xi(\alpha^R),i,\xi(\beta) \|:=2^{\xi(\alpha^R)}3^i5^{\xi(\beta)}$で表し、$\pi_k(x_1){:=}[\mu_\le(x_1\bmod k^x)](x_1,x_1)\dot{-}1$ (素数$k$の$x_1$に対する指数、$\pi_k(0){=}0$)とおけば、$\pi_2(\|x,y,z\|){=}x,$ $\pi_3(\| x,y,z\|){=}y,$ $\pi_5(\| x,y,z\|){=}z$となる。$\alpha q_i\beta\vdash \alpha' q_{i'}\beta'\drarrow M_\vdash(\Xi(\alpha q_i\beta))=\Xi(\alpha' q_{i'}\beta')$を満たす$\mathcal{PR}$ $M_\vdash(x)$は
$M_{\sigma}(x){:=}\begin{cases} \| \pi_2(x){\times}p{+}j',i',\pi_5(x){\div}p \| & \dlarrow \sigma{=}(X_{j'},R,q_{i'})\\ \| \pi_2(x){\div}p,i',(\pi_2(x){\bmod}p){+}p{\times}(j'{+}p{\times}(\pi_5(x){\div}p))\| & \dlarrow \sigma{=}(X_{j'},L,q_{i'})\\ 0 & \dlarrow x{=}0 \vee \sigma{=}\emptyset \end{cases}$
$M_\vdash(x):=[1{\le}x]{\times}\left(\sum_{i=0}^r\sum_{j=0}^{p-1}[\pi_3(x){=}i]{\times}[\pi_5(x){\bmod}p{=}j]{\times} M_{\delta(q_i,X_j)}(x)\right)$
但し$[x_1{\le}x_2]:=1\dot{-}(x_1\dot{-}x_2),$ $[x_1{=}x_2]:=[x_1{\le}x_2]{\times}[x_2{\le}x_1]$、
と書ける。簡単のため$M$は受理の際ヘッドが左端にあるとしよう。$\mathcal{PR}\ M_\vdash^*(x_1,x):=[x_1;M_\vdash(M_\vdash^*(x_1,x{-}1))]={M_\vdash}^x(x_1),\\
\mathcal{P}\mu\ M_\vdash^F(x_1):=M_\vdash^*(x_1,[\mu[\pi_3(M_\vdash^*(x_1,y)){=}r]](x_1))$ とおけば。$\mathcal{P}\mu$ $\mathfrak{M}(x){:=}\pi_5(M_\vdash^F(5^x))$ に対し $\mathfrak{M}(\xi(\vect{w})){=}\xi(M(\vect{w}))$ が成立つ。
この意味でDTMの計算は$\mathcal{P}\mu$である。後半は、前半の事実から明らか。
問．$\pi_3(2^x3^y5^z)=y,$ $[x{=}y]=\begin{cases} 1 & \dlarrow x{=}y\\ 0 & \dlarrow x{\ne}y \end{cases}$ を示せ。
問．Ackerman関数は全域関数であることを示せ。
ヒント．$m$に関する帰納法の中で$n$に関する帰納法を用いる。
DTMとの同等性
定理．$\mathcal{P}\mu$の計算能力はDTMと、$\mathcal{T}\mu$の計算能力は全入力で停止するDTMと等しい。
|
function $[\mu f](x_{1..n},x)\{$ $[\mu f]:=0;$ while$(f(x_{1..n},[\mu f]){\le}0)\{$ $[\mu f]:=[\mu f]+1\}\}$ |
|
function $[g;h](x_{1..n},x)\{$ $[g;h] := g(x_{1..n});$ for$(y{:=}1)$ to $x\ \{$ $[g;h] := h(x_{1..n},y,[g;h])\}\}$ |
逆は、一般性を失わずにDTM $M=(\{q_{0..r}\},\Sigma,\Gamma,\delta,q_0,\{q_r\}),$ $\Gamma{=}\{X_{0..p-1}\},$ $X_0{=}□$ とし、$\xi:\Gamma^*{\to}\mathbb{N}$を$\xi(\varepsilon){:=}0,\ \xi(X_j\alpha){:=}j{+}p{\times}\xi(\alpha),\ \alpha{\in}\Gamma^*$で定義すれば、$\xi(\alpha)=\xi(X_j\alpha){\div}p,$ $j=\xi(X_j\alpha)\bmod p$ だから、記号列左端での記号の取出し・追加は$\mathcal{PR}$で実現できる。※$\alpha^R$は$\xi(\alpha)$の$p$進表示で、$\xi(\alpha□^*) {=}\xi(\alpha)$が成立つ。
$M$の時点表示$\alpha q_i\beta$を自然数$\Xi(\alpha q_i\beta)=\| \xi(\alpha^R),i,\xi(\beta) \|:=2^{\xi(\alpha^R)}3^i5^{\xi(\beta)}$で表し、$\pi_k(x_1){:=}[\mu_\le(x_1\bmod k^x)](x_1,x_1)\dot{-}1$ (素数$k$の$x_1$に対する指数、$\pi_k(0){=}0$)とおけば、$\pi_2(\|x,y,z\|){=}x,$ $\pi_3(\| x,y,z\|){=}y,$ $\pi_5(\| x,y,z\|){=}z$となる。$\alpha q_i\beta\vdash \alpha' q_{i'}\beta'\drarrow M_\vdash(\Xi(\alpha q_i\beta))=\Xi(\alpha' q_{i'}\beta')$を満たす$\mathcal{PR}$ $M_\vdash(x)$は
$M_{\sigma}(x){:=}\begin{cases} \| \pi_2(x){\times}p{+}j',i',\pi_5(x){\div}p \| & \dlarrow \sigma{=}(X_{j'},R,q_{i'})\\ \| \pi_2(x){\div}p,i',(\pi_2(x){\bmod}p){+}p{\times}(j'{+}p{\times}(\pi_5(x){\div}p))\| & \dlarrow \sigma{=}(X_{j'},L,q_{i'})\\ 0 & \dlarrow x{=}0 \vee \sigma{=}\emptyset \end{cases}$
$M_\vdash(x):=[1{\le}x]{\times}\left(\sum_{i=0}^r\sum_{j=0}^{p-1}[\pi_3(x){=}i]{\times}[\pi_5(x){\bmod}p{=}j]{\times} M_{\delta(q_i,X_j)}(x)\right)$
但し$[x_1{\le}x_2]:=1\dot{-}(x_1\dot{-}x_2),$ $[x_1{=}x_2]:=[x_1{\le}x_2]{\times}[x_2{\le}x_1]$、
と書ける。簡単のため$M$は受理の際ヘッドが左端にあるとしよう。
この意味でDTMの計算は$\mathcal{P}\mu$である。後半は、前半の事実から明らか。
問．$\pi_3(2^x3^y5^z)=y,$ $[x{=}y]=\begin{cases} 1 & \dlarrow x{=}y\\ 0 & \dlarrow x{\ne}y \end{cases}$ を示せ。
$\mathcal{P}\mu$を計算するプログラムについての議論から、以下が成立つ。
$\mathfrak{U}_n(x,x_{1..n})=\begin{cases}
f(x_{1..n}) & \dlarrow x{=}\#f\\
\uparrow & それ以外
\end{cases}$
自然数と文字列の同一視
前定理では、DTMの時点表示を自然数で表しその動作を$\mathcal{PR}$で実現した。より一般的に、字母$\Gamma{=}\{a_{1..p}\}$に対し、$\widetilde{\Gamma} :a_{i_0}a_{i_1}\cdots a_{i_n}\mapsto\sum_{k=0}^n i_kp^k$は全単射で原始再帰的に計算できるから、$\vect{w}{\in}\Gamma^*$は$n{\in}\mathbb{N}$と同一視できる(の表現と見做せる)。
問．上の写像$\widetilde{\Gamma}:\Gamma^*\to\mathbb{N}$が全単射であることを示せ。
ヒント．$\vect{w}^R$は$\widetilde{\Gamma}(\vect{w})$の、$1..p$を使うある種の$p$進法になっていて、$\widetilde{\Gamma}(\varepsilon){=}0$。
この同一視により、$f:\Gamma_1^*{\times}{\cdots}{\times}\Gamma_m^*{\times}\mathbb{N}^n \to \Gamma_0^*,$ $f:\Gamma_1^*{\times}{\cdots}{\times}\Gamma_m^*{\times}\mathbb{N}^n \to \mathbb{N}$についても、$f:\mathbb{N}^{m+n}\to\mathbb{N}$と解釈して部分(全域、原始)再帰関数が定義できる。
部分再帰集合と可算帰納言語
部分再帰関数による集合(言語)の記述について押えておこう。集合$A{\subseteq}\mathbb{N}^n$に対し$a_{1..n}{\in}A \rightleftarrows [A](a_{1..n}){=}1$が成立つ$[A]:\mathbb{N}^n{\rightsquigarrow}\{0,1\}$を$A$の特徴部分関数という。
※部分関数では$a_{1..n}{\not\in}A \rightleftarrows [A](a_{1..n}){=}0$とは限らない。
集合$A{\subseteq}\mathbb{N}^n$はその特徴部分関数$[A](x_{1..n})$が$\mathcal{P}\mu_n$($\mathcal{T}\mu_n,$ $\mathcal{PR}_n$)のとき、各々$\mathcal{P}\mu_n$($\mathcal{T}\mu_n,$ $\mathcal{PR}_n$)集合であるという。この時、$\mathcal{P}\mu_n$($\mathcal{T}\mu_n,$ $\mathcal{PR}_n$)関数$f(x_{1..n})$のグラフ$\{x_{0..n}\mid x_0{=}f(x_{1..n})\}$は、その特徴部分関数が$1\dot{-}((x_0\dot{-}f(x_{1..n})){+}(f(x_{1..n})\dot{-}x_0))$と書けるので、各々$\mathcal{P}\mu_{n+1}$($\mathcal{T}\mu_{n+1},$ $\mathcal{PR}_{n+1}$)集合である。
定理．全単射$\widetilde{\Gamma}$の下で、$\mathcal{P}\mu$集合は$\Gamma$上の加算帰納言語と一致し、$\mathcal{T}\mu$集合は$\Gamma$上の判定帰納言語と一致する。
- 原始再帰はfor文を使ったプログラムで書けるので、$\mathcal{PR}$は繰返しとしてfor文のみを許すプログラムで書け、実は逆も成立つ。
- 最小化はwhile文のプログラムで書け、for文はehile文でも書けるので、$\mathcal{P}\mu$は繰返しとしてwhile文のみを許すプログラムで書け、逆も成立つ。
- $\mathfrak{M}(x)$は$\mathcal{PR}$ $f(x,y),g(x,y)$を用いて$\mathfrak{M}(x){=}f(x,[\mu g](x)])$と書けているので、$\mathcal{P}\mu$における最小化の使用は１回で済む。
- 任意のプログラムは繰返しとしてwhile文を1回使うだけの形で書ける。
自然数と文字列の同一視
前定理では、DTMの時点表示を自然数で表しその動作を$\mathcal{PR}$で実現した。より一般的に、字母$\Gamma{=}\{a_{1..p}\}$に対し、$\widetilde{\Gamma} :a_{i_0}a_{i_1}\cdots a_{i_n}\mapsto\sum_{k=0}^n i_kp^k$は全単射で原始再帰的に計算できるから、$\vect{w}{\in}\Gamma^*$は$n{\in}\mathbb{N}$と同一視できる(の表現と見做せる)。
問．上の写像$\widetilde{\Gamma}:\Gamma^*\to\mathbb{N}$が全単射であることを示せ。
ヒント．$\vect{w}^R$は$\widetilde{\Gamma}(\vect{w})$の、$1..p$を使うある種の$p$進法になっていて、$\widetilde{\Gamma}(\varepsilon){=}0$。
この同一視により、$f:\Gamma_1^*{\times}{\cdots}{\times}\Gamma_m^*{\times}\mathbb{N}^n \to \Gamma_0^*,$ $f:\Gamma_1^*{\times}{\cdots}{\times}\Gamma_m^*{\times}\mathbb{N}^n \to \mathbb{N}$についても、$f:\mathbb{N}^{m+n}\to\mathbb{N}$と解釈して部分(全域、原始)再帰関数が定義できる。
部分再帰集合と可算帰納言語
部分再帰関数による集合(言語)の記述について押えておこう。集合$A{\subseteq}\mathbb{N}^n$に対し$a_{1..n}{\in}A \rightleftarrows [A](a_{1..n}){=}1$が成立つ$[A]:\mathbb{N}^n{\rightsquigarrow}\{0,1\}$を$A$の特徴部分関数という。
※部分関数では$a_{1..n}{\not\in}A \rightleftarrows [A](a_{1..n}){=}0$とは限らない。
集合$A{\subseteq}\mathbb{N}^n$はその特徴部分関数$[A](x_{1..n})$が$\mathcal{P}\mu_n$($\mathcal{T}\mu_n,$ $\mathcal{PR}_n$)のとき、各々$\mathcal{P}\mu_n$($\mathcal{T}\mu_n,$ $\mathcal{PR}_n$)集合であるという。この時、$\mathcal{P}\mu_n$($\mathcal{T}\mu_n,$ $\mathcal{PR}_n$)関数$f(x_{1..n})$のグラフ$\{x_{0..n}\mid x_0{=}f(x_{1..n})\}$は、その特徴部分関数が$1\dot{-}((x_0\dot{-}f(x_{1..n})){+}(f(x_{1..n})\dot{-}x_0))$と書けるので、各々$\mathcal{P}\mu_{n+1}$($\mathcal{T}\mu_{n+1},$ $\mathcal{PR}_{n+1}$)集合である。
定理．全単射$\widetilde{\Gamma}$の下で、$\mathcal{P}\mu$集合は$\Gamma$上の加算帰納言語と一致し、$\mathcal{T}\mu$集合は$\Gamma$上の判定帰納言語と一致する。
チャーチ・チューリングのテーゼ
１９３０年代、様々な計算モデルが提唱され、それらの計算能力が等しいことが証明された- チューリング機械
- 再帰関数
- λ計算
- ・・・
チャーチ・チューリングのテーゼ
これらのモデルで計算できる${}\rightleftarrows{}$(理想化された)コンピュータで計算できる
${}\rightleftarrows{}$一般的な意味で計算できる
| モデル | プログラム | 計算機構 | 備考 |
| コンピュータ | 命令(機械語) | CPU＋メモリ | |
| DTM | 遷移表 | 状態＋テープ | |
| 文法 | 文法規則 | 部分文字列の置換え($\Rightarrow$) | |
| 部分再帰関数 | 再帰的定義 | 合成・原始再帰・最小化 | |
| PCP | 文字列対 | 文字列の同期 |
パズル．
１．プログラムが真の(人工)知能だとみなせる条件は何か(チューリングテスト)。
２．数学的に明確に述べられる問題は、(いずれ数学が進歩すれば)必ず解けるか。
判定不能な問題
本節では判定不能な問題が存在する事、答(出力)がyes/noの判定問題で、我々がまだ知らないという意味ではなく、それを解くプログラム(DTM)はありえない、あると矛盾するという問題が存在することを示す。しかもそれらは特殊ではなくある意味ありふれている。問題とは
まずこの章で扱う問題とそれを解くコンピュータプログラム・DTMの意味を明確に定めておこう。
- 問題は答がyes/noの判定問題である
- 問題例が無限にあり、それらは$\Sigma$上の文字列で記述される
- 答がyesの問題例を正例、noの問題例を負例と呼ぶ
- 問題の記述でない文字列は全て負例とし、正例$\dot\cup$負例${}=\Sigma^*$とする
- プログラムは$\Sigma$上の全文字列に対し、その正負(yes/no)を判定する
- DTMは、正例を受理し、負例は受理せず停止する
また、一般にプログラム・DTMは入力によって停止しない事があるが、問題を解くプログラム・DTMはすべての入力(問題例)で停止する必要がある。それを解くプログラム・DTMが無い問題は判定不能であるという。言い換えると正例(同じことだが負例)言語が判定帰納言語であるとき、判定可能である。
プログラムの停止問題
プログラム$\vect{P}$をその入力$\vect{v}{\in}\{0,1\}^*$に対して走らせたとき、いつかは停止(yes)するか否(no)かを判定する問題を停止問題という。即ち、停止問題は万能TMの記法を使って、正例${}:=\{\vect{P}\vect{v}{\in}\{0,1\}^*\mid \vect{P}は\vect{v}で停止する\}$で定義される。以下$\vect{P}$に$\vect{v}$を入力した結果(出力)を$\vect{P}(\vect{v})$と表し、停止することを$\vect{P}(\vect{v})\downarrow$、停止しないことを$\vect{P}(\vect{v})\uparrow$と表す。
定理．停止問題は判定不能であり、停止問題の正例は判定帰納言語ではない。
略証．停止問題を解くプログラム$\vect{H}(\vect{Pv})$から下図のプログラム$\vect{H}'(\vect{w})$を作ると、
.JPG)
- $\vect{H}'(\vect{w})\uparrow \vee \vect{H}'(\vect{w}){=}\rm{no}$ が成立ち
- $\vect{H}'(\vect{w})\uparrow{}\rlarrow \vect{H}(\vect{w}\vect{w}){=}\rm{yes} \rlarrow \vect{w}(\vect{w}) \downarrow$
- $\vect{H}'(\vect{w}){=}\rm{no}\rlarrow\vect{H}(\vect{w}\vect{w}){=}\rm{no} \rlarrow \vect{w}(\vect{w}) \uparrow$
${}\rlarrow \vect{H}(\vect{H}'\vect{H}'){=}\rm{yes}\rlarrow \vect{H}'(\vect{H}'){=}\rm{no}$となり矛盾。
問．「プログラム$P$を入力$\vect{w}$の下で実際に走らせる」こと（万能TM ${\mathcal U}$）では停止問題を解けない。何故か？
ライスの定理
問題の文字集合を$\Sigma$とする。答えがすべてyes(正例${=}\Sigma^*$)、あるいはすべてno(負例${=}\Sigma^*$)である問題を自明な問題という。プログラム$\vect{P},\vect{P'}$は、同じ入力に対し(停止しないことも含めて)同じ出力になるとき、働きが等しいといい$\vect{P}(\vect{x}){=}\vect{P'}(\vect{x})$と表す。働き$\vect{P}(\vect{x})$が等しいプログラムに対しては答(yes/no)が等しくなる問題をプログラムの働きに関する問題という。
問．$\vect{P} \equiv \vect{P'}$は2つのプログラムが文字列として(記述が)等しいことを表す。$\vect{P}{\equiv}\vect{P}' \darrow{\rightarrow}{\not\leftarrow}\vect{P}(\vect{x}){=}\vect{P'}(\vect{x})$ を示せ。
定理．プログラムの働きに関する問題は、自明なものを除いて判定不能である。
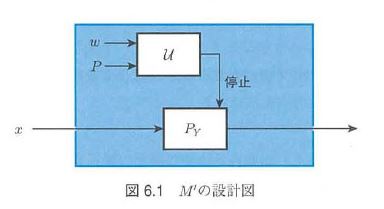略証．プログラムの働きに関する自明でない問題を解くプログラム$\vect{M}(\vect{x})$があるとする。決して停止しないプログラム$\vect{P}_0(\vect{x})$と、$\vect{M}(\vect{P}_0){\ne}\vect{M}(\vect{P}_1)$を満たすプログラム$\vect{P}_1(\vect{x})$を選ぶ。
プログラム$\vect{M}$から停止問題を解くプログラム$\vect{H}(\vect{Pv})$が作れることを示す。$\vect{H}(\vect{Pv})$は、図に示したプログラム$\vect{M}_\vect{Pv}$を作成し、$\vect{M}(\vect{M}_\vect{Pv})$を計算する。$\vect{M}_\vect{Pv}(\vect{x})$は、まず万能プログラム$\mathcal{U}$で$\vect{P}(\vect{v})$の動作を模倣し、それが停止したら$\vect{P}_1(\vect{x})$の計算を開始するプログラムである。以下が成立つ。
$\vect{P}(\vect{v})\downarrow\ \rightleftarrows \vect{M}_\vect{Pv}(\vect{x}){=}\vect{P}_1(\vect{x})\rightleftarrows \vect{H}(\vect{Pv}){=}\vect{M}(\vect{M}_\vect{Pv}){=}\vect{M}(\vect{P}_1)\\
\vect{P}(\vect{v})\uparrow\ \rightleftarrows \vect{M}_\vect{Pv}(\vect{x}){=}\vect{P}_0(\vect{x})\rightleftarrows \vect{H}(\vect{Pv}){=}\vect{M}(\vect{M}_\vect{Pv}){=}\vect{M}(\vect{P}_0)$
よって、$\vect{P}(\vect{v})$が停止するか否か判定でき矛盾するから、$M$は存在しない。
部分再帰関数での議論
解けない問題に関する議論の概略を$\mathcal{P}\mu$上で再考する。
1. 万能$\mathcal{P}\mu_{n+1}$関数$\mathfrak{U}_n(x,x_{1..n})$の定義域を拡張した$\mathcal{T}\mu_{n+1}$ $g(x,x_{1..n})$は存在しない。$\because$ 存在したとすれば$\mathcal{T}\mu_n$ $g'(x_{1..n}){:=}g(x_1,x_{1..n}){+}1$に対し $g'(\#g',x_{2..n}){=}\mathfrak{U}_n(\#g',\#g',x_{2..n}){=}g(\#g',\#g',x_{2..n}){=}g'(\#g',x_{2..n}){-}1$ より矛盾。
2.(停止問題) 全域関数$H_n(x,x_{1..n}):=\begin{cases}1 & \dlarrow \mathfrak{U}_n(x,x_{1..n})\downarrow\\ 0 & それ以外\end{cases}$は、それを使えば$\mathfrak{U}_n(x,x_{1..n})$の全域的拡張が得られるから、再帰的でない。
3.(パラメータ定理) $\mathfrak{U}_{m+n}(x,x_{1..m},y_{1..n})=\mathfrak{U}_n(\sigma_{m,n}(x,x_{1..m}),y_{1..n})$、即ち$\sigma_{m,n}(\#f(x_{1..m},y_{1..n}),a_{1..m})=\#f(a_{1..m},y_{1..n})$を満たす$\mathcal{PR}_{1+m}$ $\sigma_{m,n}$がある。
4.(不動点定理) $\mathcal{T}\mu_1\ f(x)$に対し$\mathfrak{U}_n(a,x_{1..n})=\mathfrak{U}_n(f(a),x_{1..n})$を満たす$a$がある。
$\because b{:=}\#\mathfrak{U}_{1+n}(x_0,x_{0..n})$に対し$\mathfrak{U}_n(\sigma_{1,n}(b,x_0),x_{1..n}){=}\mathfrak{U}_{1+n}(b,x_{0..n}){=}\mathfrak{U}_{1+n}(x_0,x_{0..n})$。
$c{:=}\#\mathfrak{U}_n(f(\sigma_{1,n}(b,x_0)),x_{1..n})$に対し$\mathfrak{U}_{1+n}(c,x_{0..n}){=}\mathfrak{U}_n(f(\sigma_{1,n}(b,x_0)),x_{1..n})$。
よって $\mathfrak{U}_n(f(\sigma_{1,n}(b,c)),x_{1..n}){=}\mathfrak{U}_{1+n}(c,c,x_{1..n}){=}\mathfrak{U}_n(\sigma_{1,n}(b,c),x_{1..n})$
5.(ライスの定理) $n{\gt}0$とする。次の2条件を満たす全域関数$f(x)$は$\mathcal{T}\mu$でない。 ① $\forall k\forall l. \mathfrak{U}_{1+n}(k,x_{1..n}){=}\mathfrak{U}_{1+n}(l,x_{1..n})\drarrow f(k){=}f(l),$ ② $\exists k\exists l. f(k){\lt}f(l)$。
$\because$ ②の$k,l$をとり、$g(x):=\begin{cases} l & \dlarrow f(x){\le}f(k)\\ k & \dlarrow f(k){\lt}f(x)\end{cases}$ とおけば、$\forall x.f(g(x))\ne f(x)$。$f(x)$が$\mathcal{T}\mu$なら$g(x)$も$\mathcal{T}\mu$で、4.より$\mathfrak{U}_n(a,x_{1..n})=\mathfrak{U}_n(g(a),x_{1..n})$を満たす$a$があるから、①より$f(a){=}f(g(a))$となり矛盾する。※①の条件は$f(x)$がプログラム(のコード)を入力とし、その働きに関する関数であることを意味する。
問題の文字集合を$\Sigma$とする。答えがすべてyes(正例${=}\Sigma^*$)、あるいはすべてno(負例${=}\Sigma^*$)である問題を自明な問題という。プログラム$\vect{P},\vect{P'}$は、同じ入力に対し(停止しないことも含めて)同じ出力になるとき、働きが等しいといい$\vect{P}(\vect{x}){=}\vect{P'}(\vect{x})$と表す。働き$\vect{P}(\vect{x})$が等しいプログラムに対しては答(yes/no)が等しくなる問題をプログラムの働きに関する問題という。
問．$\vect{P} \equiv \vect{P'}$は2つのプログラムが文字列として(記述が)等しいことを表す。$\vect{P}{\equiv}\vect{P}' \darrow{\rightarrow}{\not\leftarrow}\vect{P}(\vect{x}){=}\vect{P'}(\vect{x})$ を示せ。
定理．プログラムの働きに関する問題は、自明なものを除いて判定不能である。
略証．プログラムの働きに関する自明でない問題を解くプログラム$\vect{M}(\vect{x})$があるとする。決して停止しないプログラム$\vect{P}_0(\vect{x})$と、$\vect{M}(\vect{P}_0){\ne}\vect{M}(\vect{P}_1)$を満たすプログラム$\vect{P}_1(\vect{x})$を選ぶ。プログラム$\vect{M}$から停止問題を解くプログラム$\vect{H}(\vect{Pv})$が作れることを示す。$\vect{H}(\vect{Pv})$は、図に示したプログラム$\vect{M}_\vect{Pv}$を作成し、$\vect{M}(\vect{M}_\vect{Pv})$を計算する。$\vect{M}_\vect{Pv}(\vect{x})$は、まず万能プログラム$\mathcal{U}$で$\vect{P}(\vect{v})$の動作を模倣し、それが停止したら$\vect{P}_1(\vect{x})$の計算を開始するプログラムである。以下が成立つ。
部分再帰関数での議論
解けない問題に関する議論の概略を$\mathcal{P}\mu$上で再考する。
1. 万能$\mathcal{P}\mu_{n+1}$関数$\mathfrak{U}_n(x,x_{1..n})$の定義域を拡張した$\mathcal{T}\mu_{n+1}$ $g(x,x_{1..n})$は存在しない。$\because$ 存在したとすれば$\mathcal{T}\mu_n$ $g'(x_{1..n}){:=}g(x_1,x_{1..n}){+}1$に対し $g'(\#g',x_{2..n}){=}\mathfrak{U}_n(\#g',\#g',x_{2..n}){=}g(\#g',\#g',x_{2..n}){=}g'(\#g',x_{2..n}){-}1$ より矛盾。
2.(停止問題) 全域関数$H_n(x,x_{1..n}):=\begin{cases}1 & \dlarrow \mathfrak{U}_n(x,x_{1..n})\downarrow\\ 0 & それ以外\end{cases}$は、それを使えば$\mathfrak{U}_n(x,x_{1..n})$の全域的拡張が得られるから、再帰的でない。
3.(パラメータ定理) $\mathfrak{U}_{m+n}(x,x_{1..m},y_{1..n})=\mathfrak{U}_n(\sigma_{m,n}(x,x_{1..m}),y_{1..n})$、即ち$\sigma_{m,n}(\#f(x_{1..m},y_{1..n}),a_{1..m})=\#f(a_{1..m},y_{1..n})$を満たす$\mathcal{PR}_{1+m}$ $\sigma_{m,n}$がある。
4.(不動点定理) $\mathcal{T}\mu_1\ f(x)$に対し$\mathfrak{U}_n(a,x_{1..n})=\mathfrak{U}_n(f(a),x_{1..n})$を満たす$a$がある。
$\because b{:=}\#\mathfrak{U}_{1+n}(x_0,x_{0..n})$に対し$\mathfrak{U}_n(\sigma_{1,n}(b,x_0),x_{1..n}){=}\mathfrak{U}_{1+n}(b,x_{0..n}){=}\mathfrak{U}_{1+n}(x_0,x_{0..n})$。
$c{:=}\#\mathfrak{U}_n(f(\sigma_{1,n}(b,x_0)),x_{1..n})$に対し$\mathfrak{U}_{1+n}(c,x_{0..n}){=}\mathfrak{U}_n(f(\sigma_{1,n}(b,x_0)),x_{1..n})$。
よって $\mathfrak{U}_n(f(\sigma_{1,n}(b,c)),x_{1..n}){=}\mathfrak{U}_{1+n}(c,c,x_{1..n}){=}\mathfrak{U}_n(\sigma_{1,n}(b,c),x_{1..n})$
5.(ライスの定理) $n{\gt}0$とする。次の2条件を満たす全域関数$f(x)$は$\mathcal{T}\mu$でない。 ① $\forall k\forall l. \mathfrak{U}_{1+n}(k,x_{1..n}){=}\mathfrak{U}_{1+n}(l,x_{1..n})\drarrow f(k){=}f(l),$ ② $\exists k\exists l. f(k){\lt}f(l)$。
$\because$ ②の$k,l$をとり、$g(x):=\begin{cases} l & \dlarrow f(x){\le}f(k)\\ k & \dlarrow f(k){\lt}f(x)\end{cases}$ とおけば、$\forall x.f(g(x))\ne f(x)$。$f(x)$が$\mathcal{T}\mu$なら$g(x)$も$\mathcal{T}\mu$で、4.より$\mathfrak{U}_n(a,x_{1..n})=\mathfrak{U}_n(g(a),x_{1..n})$を満たす$a$があるから、①より$f(a){=}f(g(a))$となり矛盾する。※①の条件は$f(x)$がプログラム(のコード)を入力とし、その働きに関する関数であることを意味する。
判定不能問題２
| i | xi | yi |
| 1 | 10 | 101 |
| 2 | 011 | 11 |
| 3 | 101 | 011 |
| i | xi | yi |
| 1 | 1 | 111 |
| 2 | 10111 | 10 |
| 3 | 10 | 0 |
問．右表のPCP(の実例)の解の有無を示せ。
定理．Postの対応問題は判定不能である。
略証．アイディアは文法$G=(\Sigma,\Gamma,P,S)$の導出列が解になるようなPCPを作ることである。 PCP $\mathcal{P}=(\#,\#S{\overset{*}{\Rightarrow}})\bigodot_{X\in\Sigma\dot\cup\Gamma\dot\cup\{\overset{*}{\Rightarrow}\}}(X,X)\bigodot_{\alpha{\to}\beta{\in}P}(\alpha,\beta)\cdot({\overset{*}{\Rightarrow}}\vect{w}\#,\#)$ の最初の対$(\#,\#S{\overset{*}{\Rightarrow}})$から始まる解は、第2項が構成する列が第1項が構成する列より常に先行し、$\vect{w}$が生成されると最後の対を適用して、解になる。すなわち
$\#S{\overset{*}{\Rightarrow}}\alpha_1{\overset{*}{\Rightarrow}}\alpha_2{\overset{*}{\Rightarrow}}\cdots{\overset{*}{\Rightarrow}}\vect{w}\#$が解ならば、$S{\overset{*}{\Rightarrow}}\alpha_1{\overset{*}{\Rightarrow}}\alpha_2{\overset{*}{\Rightarrow}}\cdots{\overset{*}{\Rightarrow}}\vect{w}$である。
解決すべき点が2点ある。まず、PCPの文字集合は有限の定集合だから、文法によって増える$\Sigma\dot\cup\Gamma$の記号をそのままは使えない。次に、$\mathcal{P}$は自明な解 ${\overset{*}{\Rightarrow}}$ を持つから、解が必ず最初の対から始まるように制限する必要がある。そのために、$\Delta{=}\{X_1,X_2,\dots,X_m\}$上のPCP $\mathcal{P}_1=\bigodot_{i=1}^k(\vect{x}_i,\vect{y}_i)$ に対し、2つの準同型写像$\Delta^*{\to}\{0,1\}^*$を $h_1:X_i\mapsto 0^i1,\ {}_1h:X_i\mapsto 10^i$ で定義する。
PCP$(1h_1(\vect{x}_1),{}_1h(\vect{y}_1))\bigodot_{j=1}^k(h_1(\vect{x}_j),{}_1h(\vect{y}_j))\cdot (1,11)$の解は$1h_1(\vect{w})1{=}{}_1h(\vect{w})11$を満たし、$\vect{w}$は$\mathcal{P}_1$の第1対$(\vect{x}_1,\vect{y}_1)$から始まる解である。
問．２つのCFLの共通部分が空か否かは判定不能であることを示せ。
ヒント．PCPが解を持つ ${}\rightleftarrows L_1{\cap}L_2{\ne}\emptyset$、となるように、CFL$L_1,L_2$を定めよ。
ヒルベルトの第10問題 は、整係数の多変数多項式の方程式(ディオファントス方程式)が整数解を持つか否かの判定問題である。例えば、$x^2+y^2=z^2$ は無限の整数会$(0,0,0),(3,4,5),(5,12,13),\dots$をもち、$(x^2+1)^3+(y^2+1)^3=z^3$の整数解はフェルマの最終定理より存在しない。
ヒルベルトの第10問題は、任意の部分再帰集合$A$に対し、ある整係数多項式$P(x,x_{1..9})$が存在して$A=\{x \mid \exists x_{1..9} (x,x_{1..9}){=}0\}$と表せる(マチャセビッチ)から判定不能だが、その証明は本稿の範囲を超えるので省略する。
論理式による表現
第0章では自然数上の$+,\le$を持つ1階述語論理(プレスバーガー算術)が記述する集合が準線形集合と一致した。本節では、自然数数上の$+,\times,\le$を持つ1階述語論理と部分再帰集合の関係を調べる。和と積を持つ論理
自然数上の1階述語論理$\mathfrak{N}$の項、論理式を再帰的に以下で定義する。
1.自然数$a({\in}\mathbb{N})$、変数$x,x_1,x_2,\dots$は項、
2. $t_1,t_2$が項なら$(t_1+t_2),(t_1\times t_2)$は項、$(t_1{\le}t_2)$は論理式
3.$\varphi,\psi$が論理式なら$\neg\varphi,(\varphi{\wedge}\psi),\forall x\varphi$も論理式
なお本文の記述では読み易さのために()を適宜調整し、以下の略記等を使う。
$\forall x_{1..n}\varphi:\equiv \forall x_1\dots\forall x_n\varphi,$ $\exists x_{1..n}\varphi:\equiv \neg\forall x_{1..n}\neg\varphi,$
※以下で使われる$y,z,x_0$等の変数は適宜、上記の変数のどれかであるとする。
$\Delta_0$式$\varphi$と存在(全称)量化$\exists x_{1..n}\varphi\ (\forall x_{1..n}\varphi)$で表せる論理式を各々$\Sigma_1$($\Pi_1$)式という。論理式$\varphi$が(必要なら変数名を付け替えて)自由変数$x_{1..n}$を持つ時、$\varphi(x_{1..n})$と表し、$n{=}0$のとき$\varphi(){\equiv}\varphi$を命題という。論理式$\varphi(x_{1..n})$はそれを成立たせる値の集合$\varphi^\top{:=}\{a_{1..n}\mid \varphi(a_{1..n})\}\subseteq\mathbb{N}^n$を表す。$\Delta_0\ (\Sigma_1,\Pi_1)$論理式が表す集合を各々$\Delta_0\ (\Sigma_1,\Pi_1)$集合といい、$\Sigma_1$かつ$\Pi_1$の集合を$\Delta_1$集合という。
以下、α集合(言語)のクラスを$\mathfrak{C}(\alpha)$と表す。
定理．$\mathfrak{C}(\Delta_0)\subseteq \mathfrak{C}({\mathcal{PR}})$、$\mathfrak{C}(\Sigma_1)\subseteq \mathfrak{C}(\mathcal{P}\mu)$。
略証．論理式$\varphi(x_{1..n})$に対し、$\varphi$が表す集合$\varphi^\top$の特徴部分関数$[\varphi](x_{1..n})$を構成する。$[t_1{\le}t_2]{:=}1\dot{-}(t_1\dot{-}t_2)$は$t_1,t_2$は和や積で書け$\mathcal{PR}$である。$[\varphi],$$[\psi]$が$\mathcal{PR}$なら、$[\varphi{\wedge}\psi]{:=}[\varphi]{\times}[\psi],$ $[\neg\varphi]{:=}1\dot{-}[\varphi],$ $[\forall x_1{\le}x(\varphi)](x,x_{2..n}){:=}\prod_{x_1=0}^x [\varphi](x_{1..n})$も$\mathcal{PR}$なので、$\Delta_0$集合は$\mathcal{PR}$集合である。
$[\varphi](x_{1..n},x)$が$\mathcal{P}\mu$関数なら$[\exists x\varphi](x_{1..n},x){:=}(1\dot{-}([\mu[\varphi]](x_{1..n}){+}1)){+}1$も$\mathcal{P}\mu$関数。
$\mathfrak{C}(\mathcal{P}\mu)=\mathfrak{C}(\Sigma_1)$、即ち$\mathfrak{C}(\mathcal{P}\mu)\subseteq \mathfrak{C}(\Sigma_1)$を示すために、以下の補題を示す。
※青字の論理表現は$\rightleftarrows$で結ばれた論理式の説明で、$\mathfrak{N}$の論理式ではない。
補題．全単射$\langle x_{0..1}\rangle$と単射$\langle\cdot\rangle_*:\mathbb{N}^*{\to}\mathbb{N}$、$\Delta_0$式$\pi(x_{1..3}),$ $\pi_*(x_{1..3})$が存在して $\pi(\langle x_{0..1}\rangle,i,a) \color{blue}{\rightleftarrows i{\le}1 \wedge a_i{=}a{\le}\langle x_{0..1}\rangle},$ $\pi_*(\langle a_{0..n}\rangle_*,i,a) \color{blue}{\rightleftarrows i{\le}n \wedge a_i{=}a{\le}\langle a_{0..n}\rangle_*}$
略証．$\mathfrak{N}$の項$t_\pi(x_{0..1}){:\equiv}(x_0{+}x_1){\times}(x_0{+}x_1{+}1){+}2{\times}x_0$に対し$\langle x_{0..1}\rangle{:=}t_\pi(x_{0..1}){\div}2$ は全単射で、$y{=}\langle x_{0..1}\rangle :\equiv 2{\times}y{=}t_\pi(x_{0..1})$は$\Delta_0$式である。$\pi(x_{1..3})$は次式で定める。
問．1. $p(x,y){=}(x{+}y)(x{+}y{+}1){\div}2+x$ は全単射であることを示せ。
2. $m!(k{+}1){+}1,\ 0{\le}k{\le}m$ は互いに素、を示せ。
3. $k\in D \rightleftarrows (\max D)!(k{+}1){+}1) | \prod_{j\in D}((\max D)!(j{+}1){+}1)$ を示せ。
定理．$\mathfrak{C}(\mathcal{P}\mu)\subseteq \mathfrak{C}(\Sigma_1)$
略証．$\mathcal{P}\mu$関数$f(x_{1..n})$に対し、$\Sigma_1$式$y{=}f(x_{1..n})$を帰納的に以下で定義すれば、$\mathcal{P}\mu$集合$A{\subseteq}\mathbb{N}^n$の特徴$\mathcal{P}\mu$関数$f_A(x_{1..n})$に対し$\Sigma_1$式$1{=}f_A(x_{1..n})$が$A$を表す。
以上をまとめて、次を得る。
定理．1. $\mathfrak{C}(\mathcal{P}\mu)=\mathfrak{C}(\Sigma_1)=\mathfrak{C}(可算帰納)$、$\mathfrak{C}(\mathcal{T}\mu)=\mathfrak{C}(\Delta_1)=\mathfrak{C}(判定帰納)$
2. $\mathfrak{C}(\Sigma_1)\supset\mathfrak{C}(\Delta_1){=}\mathfrak{C}(\Sigma_1){\cap}\mathfrak{C}(\Pi_1)\subset\mathfrak{C}(\Pi_1)$
本講義の主題である文法やオートマトン(さらに$\mathcal{P}\mu$関数やコンピュータプログラム等)で表せる可算帰納な集合(言語)は$\Sigma_1$であるが、$\mathfrak{N}$の論理式はより複雑な集合を表せる。実際、$k{\ge}1$の$\Sigma_k\ (\Pi_k)$式$\varphi$に対し$\forall x_{1..m}\varphi\ (\exists x_{1..m}\varphi)$を各々$\Pi_{k+1}\ (\Sigma_{k+1})$式といい、$\Sigma_k\ (\Pi_k)$式$\psi(x_{1..n})$が表す集合を各々$\Sigma_k\ (\Pi_k)$集合とすれば次が成立つ(証明は省略する)。
定理．$\mathfrak{C}(\Sigma_k)\vee \mathfrak{C}(\Pi_k) \subset \mathfrak{C}(\Sigma_{k+1})\cap \mathfrak{C}(\Pi_{k+1})$
$\mathfrak{N}$の項$t$や論理式$\varphi$に対し、$a{\in}\mathbb{N},\ x_i$を各々文字列$\underline{a}{:=}01^a,\ \underline{x_i}{:=}x0^i$で表した$\underline{t},$ $\underline{\varphi}$は字母$\Gamma{:=}\{0,1,(,),x,+,\times,\le,\wedge,\neg,\forall\}$上の文字列で、$\underline{\varphi}(x_{1..n}):a_{1..n}\mapsto \underline{\varphi(a_{1..n})}$は$\mathcal{PR}$関数$:\mathbb{N}^n{\to}\Gamma^*$である(パラメータ定理)。
補題．論理式$\varphi(x_{1..n})$と$\Sigma_i$($\Pi_i$)言語$L{\subseteq}\Gamma^*$に対し、$\underline{\varphi}^{-1}(L)$は各々$\Sigma_i$($\Pi_i$)集合。
証明．$\vect{w}{=}\underline{\varphi}(x_{1..n})$は$\Delta_0$式である。$L$を表す式を$\vect{w}{\in}L$と書けば$a_{1..n}{\in}\underline{\varphi}^{-1}(L)
\rightleftarrows \exists \vect{w}(\vect{w}{=}\underline{\varphi}(a_{1..n}){\wedge}\vect{w}{\in}L)
\rightleftarrows \forall \vect{w}(\vect{w}{=}\underline{\varphi}(a_{1..n}){\to}\vect{w}{\in}L)$
ここで$\vect{w}{\in}L$が各々$\Sigma_i$($\Pi_i$)式なら、中央(最後)の論理式は$\Sigma_i$($\Pi_i$)式である。
これまで命題$\varphi$が成立つことを単に$\varphi$と表してきたが、適宜、その真($\top$)偽($\bot$)を$\varphi{\circeq}\top,$ $\varphi{\circeq}\bot$で表し、真偽が一致することを$\varphi{\circeq}\psi$と表す。
定理．$\pmb{\top}{:=}\{\underline{\varphi} \mid \varphi{\circeq}\top \}\subseteq\Gamma^*$は$\mathfrak{N}$の式で定義できない。
証明．$\pmb{\top}$が$\Sigma_i$($\Pi_i$)言語なら、任意の論理式$\varphi(x)$に対し$\varphi^{-1}(\pmb{\top}){=}\{a\mid\varphi(a)\}{=}\varphi(x)^\top$が$\Sigma_i$($\Pi_i$)集合となるから矛盾。
2. $m!(k{+}1){+}1,\ 0{\le}k{\le}m$ は互いに素、を示せ。
3. $k\in D \rightleftarrows (\max D)!(k{+}1){+}1) | \prod_{j\in D}((\max D)!(j{+}1){+}1)$ を示せ。
定理．$\mathfrak{C}(\mathcal{P}\mu)\subseteq \mathfrak{C}(\Sigma_1)$
略証．$\mathcal{P}\mu$関数$f(x_{1..n})$に対し、$\Sigma_1$式$y{=}f(x_{1..n})$を帰納的に以下で定義すれば、$\mathcal{P}\mu$集合$A{\subseteq}\mathbb{N}^n$の特徴$\mathcal{P}\mu$関数$f_A(x_{1..n})$に対し$\Sigma_1$式$1{=}f_A(x_{1..n})$が$A$を表す。
- $y{=}s(x_1):\equiv y{=}x_1{+}1$、$y{=0}:\equiv y{=}0$、$y{=}p_{n,i}(x_{1..n}):\equiv y{=}x_i$。
- $y{=}f(g_{1..m})(x_{1..n}):\equiv \exists u\exists u_{1..m}{\le}u.\left(\bigwedge_{i=1}^m u_i{=}g_i(x_{1..n})\wedge y{=}f(u_{1..m})\right)$、
- $y{=}[g;h](x_{1..n},x)\ \ \color{blue}{\rightleftarrows \exists u \forall t{\le}x. \left(\pi_*(u,t,[g;h](x_{1..n},t))\wedge \pi_*(u,x,y)\right)}\\ :\equiv \exists u\exists v{\le}u.\left(v{=}g(x_{1..n})\wedge \pi_*(u,0,v)\wedge \pi_*(u,x,y)\wedge \\ \forall t{\lt}y\exists p{\le}u\exists q{\le}u.\left( \pi_*(u,t,p)\wedge \pi_*(u,t{+}1,q)\wedge q{=}h(x_{1..n},t,p)\right)\right)。$
- $y{=}[\mu f](x_{1..n}):\equiv \forall t{\lt}y.\left(0{=}f(x_{1..n},t) \wedge \neg 0{=}f(x_{1..n},y)\right)$。
以上をまとめて、次を得る。
定理．1. $\mathfrak{C}(\mathcal{P}\mu)=\mathfrak{C}(\Sigma_1)=\mathfrak{C}(可算帰納)$、$\mathfrak{C}(\mathcal{T}\mu)=\mathfrak{C}(\Delta_1)=\mathfrak{C}(判定帰納)$
2. $\mathfrak{C}(\Sigma_1)\supset\mathfrak{C}(\Delta_1){=}\mathfrak{C}(\Sigma_1){\cap}\mathfrak{C}(\Pi_1)\subset\mathfrak{C}(\Pi_1)$
本講義の主題である文法やオートマトン(さらに$\mathcal{P}\mu$関数やコンピュータプログラム等)で表せる可算帰納な集合(言語)は$\Sigma_1$であるが、$\mathfrak{N}$の論理式はより複雑な集合を表せる。実際、$k{\ge}1$の$\Sigma_k\ (\Pi_k)$式$\varphi$に対し$\forall x_{1..m}\varphi\ (\exists x_{1..m}\varphi)$を各々$\Pi_{k+1}\ (\Sigma_{k+1})$式といい、$\Sigma_k\ (\Pi_k)$式$\psi(x_{1..n})$が表す集合を各々$\Sigma_k\ (\Pi_k)$集合とすれば次が成立つ(証明は省略する)。
定理．$\mathfrak{C}(\Sigma_k)\vee \mathfrak{C}(\Pi_k) \subset \mathfrak{C}(\Sigma_{k+1})\cap \mathfrak{C}(\Pi_{k+1})$
$\mathfrak{N}$の項$t$や論理式$\varphi$に対し、$a{\in}\mathbb{N},\ x_i$を各々文字列$\underline{a}{:=}01^a,\ \underline{x_i}{:=}x0^i$で表した$\underline{t},$ $\underline{\varphi}$は字母$\Gamma{:=}\{0,1,(,),x,+,\times,\le,\wedge,\neg,\forall\}$上の文字列で、$\underline{\varphi}(x_{1..n}):a_{1..n}\mapsto \underline{\varphi(a_{1..n})}$は$\mathcal{PR}$関数$:\mathbb{N}^n{\to}\Gamma^*$である(パラメータ定理)。
補題．論理式$\varphi(x_{1..n})$と$\Sigma_i$($\Pi_i$)言語$L{\subseteq}\Gamma^*$に対し、$\underline{\varphi}^{-1}(L)$は各々$\Sigma_i$($\Pi_i$)集合。
証明．$\vect{w}{=}\underline{\varphi}(x_{1..n})$は$\Delta_0$式である。$L$を表す式を$\vect{w}{\in}L$と書けば
これまで命題$\varphi$が成立つことを単に$\varphi$と表してきたが、適宜、その真($\top$)偽($\bot$)を$\varphi{\circeq}\top,$ $\varphi{\circeq}\bot$で表し、真偽が一致することを$\varphi{\circeq}\psi$と表す。
定理．$\pmb{\top}{:=}\{\underline{\varphi} \mid \varphi{\circeq}\top \}\subseteq\Gamma^*$は$\mathfrak{N}$の式で定義できない。
証明．$\pmb{\top}$が$\Sigma_i$($\Pi_i$)言語なら、任意の論理式$\varphi(x)$に対し$\varphi^{-1}(\pmb{\top}){=}\{a\mid\varphi(a)\}{=}\varphi(x)^\top$が$\Sigma_i$($\Pi_i$)集合となるから矛盾。
ゲーデルの不完全性定理
本節では、$\mathfrak{N}$の項や論理式は前節の最後で記述した$\underline{t},\ \underline{\varphi}$の形式で書かれているものとし、特に断らない限り下線は省略するとともに、論理式を記述する字母$\Gamma$の文字列$\vect{w}$を時に応じて自然数$\widetilde{\Gamma}(\vect{w})$と見做す。これにより、$\mathfrak{N}$の論理式は文字列(論理式)に関する述語とも見做せて、例えば$\varphi{\circeq}\psi(\widetilde{\Gamma}(\varphi))$を単に$\varphi{\circeq}\psi(\varphi)$と表す。ゲーデル文
定理．$\mathfrak{N}$の論理式$\Psi(x)$に対し、
1.$G_\Psi{\circeq}\neg\Psi(G_\Psi)$を満たす命題$G_\Psi$(ゲーデル文という)が構成できる。
2.$\Psi^\top{\subseteq} \pmb{\top}$なら$\Psi(G_\Psi)\circeq \Psi(\neg G_\Psi)\circeq\bot$。
証明．1.変数$x$に関する論理式全体の(原始再帰的な)番号付けを次のようにおき、
2.$\Psi(G_\Psi) \drarrow$ $\neg\Psi(G_\Psi){\circeq} G_\Psi{\in}\Psi^\top {\subseteq}\pmb{\top} $ より矛盾。
$\Psi(\neg G_\Psi) \drarrow$ $\Psi(G_\Psi){\circeq} \neg G_\Psi{\in}\Psi^\top {\subseteq}\pmb{\top} \drarrow$ $G_\Psi$ より矛盾。
①例えば$\varphi_0{\equiv}\varphi_1{\equiv}x{\le}0,\dots,\varphi_{011|x}{\equiv}011|x$なら、$\psi(0){\circeq}\neg\Psi(\varphi_0(0)){\equiv}\neg\Psi(0{\le}0),$ $\psi(1){\circeq}\neg\Psi(\varphi_1(1)){\equiv}\neg\Psi(01{\le}0),$ $\psi(011|x){\circeq}\neg\Psi(\varphi_{011|x}(011|x)){\equiv}\neg\Psi(011|01^{011|x})$。
$\mathfrak{N}$の命題の集合$P$は、$P\subseteq\pmb{\top}$のとき健全であるといい、任意の命題$\varphi$に対し$\varphi$か$\neg\varphi$の一方は$P$に属すとき完全であるという。健全で完全な命題集合は正しく$\pmb{\top}$だから、上の定理の2.から次が言えて、前節の最後の定理の別証になる。
定理．命題の健全な$\mathfrak{N}$定義集合は不完全であり、$\pmb{\top}$を表す$\mathfrak{N}$論理式は無い。
第一不完全性定理
形式体系とは（ユークリッド原論のように）公理という命題(の集合)に推論規則を適用して定理という命題を導く(生成する)システムである。$\varphi$が形式体系で導かれる事を${\vdash}\varphi$と表し、定理の集合を$\mathfrak{Th}:=\{\varphi\mid\;\vdash\varphi\}$と表す。本節では、$\mathfrak{N}$の形式体系$\vdash$の詳細に立ちいる事はしないが、以下を仮定する。
- $\mathfrak{Th}:=\{\varphi\mid{}\vdash\varphi\}$は可算帰納言語($\Sigma_1$集合)である。
-
各$m,n{\in}\mathbb{N}$に対し、$\vdash 01^m{+}01^n{=}01^{m+n},$ $\vdash 01^m{\times}01^n{=}01^{m\times n},$ $m{\le}n\drarrow{}\vdash (01^m{\le}01^n),$ $m{\gt}n\drarrow{}\vdash\neg(01^m{\le}01^n),$
$\vdash \forall x(x{\le}x),$ $\vdash \forall x_{1..3}(x_1{\le}x_2{\wedge}x_2{\le}x_3){\to}x_1{\le}x_3,$ $\vdash \forall x(x{\le}01^n{\to}\bigvee_{k=0}^n x{=}01^k)$ - $\not\vdash \neg 0{\le}0$
- 論理記号$\wedge,\neg,\forall$の意味に基づいた適切な導出ができる
定理．$\Sigma_1$命題$\varphi$に対し $\varphi \drarrow {}\vdash\varphi$。$\Pi_1$命題$\psi$に対し $\vdash\psi \drarrow \psi$。
証明．$\neg\forall$を$\exists\neg$に書きかえれば、ド・モルガンの法則と2重否定の除去により、$\neg$は全て$\neg t{\le}u$の形で現れるとしてよい。$\varphi$の構成に関する帰納法で証明する。
$\mathfrak{Th}$が$\Sigma_1$集合と仮定しているから、$\vdash\vect{w} \rightleftarrows \exists y\theta(y,\vect{w}) $を満たす$\Delta_0$式$\theta(x_{1..2})$がある。$\theta(y,\vect{w})$は"命題$\vect{w}$が定理である証拠$y$"と解釈でき $\not\vdash\vect{w} \rightleftarrows \forall y\neg\theta(y,\vect{w})$。
$\Sigma_1$式$\Theta(\vect{w}):\equiv \exists y(\theta(y,\vect{w})\wedge \forall z{\le}y( \neg\theta(z,\neg\vect{w})))$とおく。
補題．任意の命題$\sigma$に対し、$\begin{cases} \vdash\sigma & \drarrow\ \vdash \Theta(\sigma)\\ \vdash\neg\sigma & \drarrow\ \vdash \neg\Theta(\sigma)\end{cases}$
証明. $\vdash \sigma$とする。$\exists y\theta(y,\sigma)$。$\vdash$は無矛盾だから、$\not\vdash \neg\sigma$より$\forall z \neg\theta(z,\neg\sigma)$。よって$\Theta(\sigma)$の定義より$\Theta(\sigma)$(が成立つ)。$\Theta(\sigma)$は$\Sigma_1$命題だから$\;\vdash\Theta(\sigma)$。
$\vdash \neg\sigma$とする。$\vdash \Theta(\neg\sigma)$より、$\vdash \theta(c,\neg\sigma)\wedge \forall z{\le}c.\neg\theta(z,\sigma)$を満たす$c$がある。よって、$\vdash \theta(y,\sigma)\to c{\lt}y$。$\vdash \theta(y,\sigma)\to \exists z{\le}y(\theta(z.\neg\sigma))$、即ち $\vdash \neg\Theta(\sigma)$。
※$\neg\Theta(\sigma)$は$\Pi_1$命題だから、$\vDash\neg\Theta(\sigma)$から $\vdash\neg\Theta(\sigma)$は言えない。
定理．$\Theta(x)$のゲーデル文$G_\Theta$に対し、$\not\vdash G_\Theta$ かつ $\not\vdash \neg G_\Theta$ かつ $G_\Theta\circeq \top$。
証明. $G_\Theta{\equiv}\psi_\Theta(\psi_\Theta){\equiv} \forall y(y=\psi_\Theta{\to} \neg\Theta(y(\psi_\Theta)))$と書けるから、$\vdash \neg G_\Theta$なら上の補題より$\vdash \neg\Theta(G_\Theta){\equiv}\neg\Theta(\psi_\Theta(\psi_\Theta))$。よって$\vdash G_\Theta$となり、矛盾。
$\vdash G_\Theta$なら、$\Pi_1$命題$G_\Theta{\circeq}\neg\Theta(G_\Theta){\equiv} \forall y(\theta(y,G_\Theta){\to}\exists z{\le}y(\theta(z,\neg G_\Theta))){\circeq}\top$で、$\theta(a,G_\Theta)$を満たす$a$に対し$\exists z{\le}a(\theta(z,\neg G_\Theta))$より$\vdash \neg G_\Theta$。これも矛盾。
$\not\vdash G_\Theta$より $\top {\circeq} \forall y(\neg\theta(y,G_\Theta)) {\circeq} \forall y(\theta(y,G_\Theta){\to}\exists z{\le}y(\theta(z,\neg G_\Theta))){\equiv}\neg\Theta(G_\Theta) {\circeq} G_\Theta$
第二不完全性定理
$\vdash$において、無矛盾性を示す命題を$\mathcal{C}{:\equiv}\forall y\neg\theta(y, \neg0{\le}0)$とおき、論理式$\varphi(x)$に対する数学的帰納法を表す命題を$\mathcal{I}_\varphi{:\equiv}(\varphi(0){\wedge}\forall x(\varphi(x){\to}\varphi(x{+}1))){\to}\forall x\varphi(x)$とおく。
定理．任意の$\Sigma_1$式$\varphi(x)$に対し$\vdash \mathcal{I }_\varphi$、ならば$\not\vdash \mathcal{C}$
略証．$\vdash \mathcal{C}$と仮定して矛盾を導く。$\vdash$では$\Sigma_1$式に対する数学的帰納法が使えるので、第一不完全性定理にいたる証明を$\vdash$の中で展開できて①、$\vdash \forall y(\neg\theta(y,G_\Theta))$、$\vdash \forall y(\neg\theta(y,\neg G_\Theta))$、$\vdash G_\Theta$②が成立つ。$\vdash G_\Theta$なら $\vdash \exists y\theta(G_\Theta)$だから、矛盾。
①$\Sigma_1$命題$\varphi$に対し、$\varphi \drarrow {}\vdash\varphi$の証明を$\vdash$で展開し、$\vdash \varphi {\to} \exists y\theta(y,\varphi)$ を導出するために、$\Sigma_1$式に対する数学的帰納法の仮定が必要になる。
②$G_\Theta{\circeq}\top$の証明を$\vdash$で展開すれば $\vdash G_\Theta$が示せる。
証明．$\neg\forall$を$\exists\neg$に書きかえれば、ド・モルガンの法則と2重否定の除去により、$\neg$は全て$\neg t{\le}u$の形で現れるとしてよい。$\varphi$の構成に関する帰納法で証明する。
- 変数を含まない項$t$はある$a{\in}\mathbb{N}$に対し$t{=}a$(が成立つこと)から、仮定のII.より${}\vdash t{=}a$。II.IV.より等号の交換・推移律が$\vdash$で導けるから、変数を含まない項$t,u$に対し、$t{\le}u \drarrow {}\vdash t{\le}u$、かつ $\neg t{\le}u \drarrow {}\vdash \neg(t{\le}u)$。
- $\varphi\wedge\psi,$ $\varphi\vee\psi$の場合、帰納法の仮定$\varphi\drarrow{}\vdash\varphi,$ $\varphi\drarrow{}\vdash\varphi$と、$\wedge,\vee$の意味から、$\vdash\varphi\wedge\psi,$ $\vdash\varphi\vee\psi$が成立つ。
- $\forall x{\le}t(\varphi(x))$の時、ある$a{\in}\mathbb{N}$について$t{=}a\wedge \bigwedge_{k=0}^a\varphi(k)$より$\;\vdash t{=}a\wedge\bigwedge_{k=0}^a\varphi(k)$。$\vdash x{\le}a\to \bigvee_{k=0}^a x{=}k$より、$\vdash \forall x{\le}t(\varphi(x))$。
- $\exists x\varphi(x)$の時、ある$a{\in}\mathbb{N}$について$\varphi(a)$より$\;\vdash\varphi(a)$。よって、$\vdash\exists x\varphi(x)$。
$\mathfrak{Th}$が$\Sigma_1$集合と仮定しているから、$\vdash\vect{w} \rightleftarrows \exists y\theta(y,\vect{w}) $を満たす$\Delta_0$式$\theta(x_{1..2})$がある。$\theta(y,\vect{w})$は"命題$\vect{w}$が定理である証拠$y$"と解釈でき $\not\vdash\vect{w} \rightleftarrows \forall y\neg\theta(y,\vect{w})$。
$\Sigma_1$式$\Theta(\vect{w}):\equiv \exists y(\theta(y,\vect{w})\wedge \forall z{\le}y( \neg\theta(z,\neg\vect{w})))$とおく。
補題．任意の命題$\sigma$に対し、$\begin{cases} \vdash\sigma & \drarrow\ \vdash \Theta(\sigma)\\ \vdash\neg\sigma & \drarrow\ \vdash \neg\Theta(\sigma)\end{cases}$
証明. $\vdash \sigma$とする。$\exists y\theta(y,\sigma)$。$\vdash$は無矛盾だから、$\not\vdash \neg\sigma$より$\forall z \neg\theta(z,\neg\sigma)$。よって$\Theta(\sigma)$の定義より$\Theta(\sigma)$(が成立つ)。$\Theta(\sigma)$は$\Sigma_1$命題だから$\;\vdash\Theta(\sigma)$。
$\vdash \neg\sigma$とする。$\vdash \Theta(\neg\sigma)$より、$\vdash \theta(c,\neg\sigma)\wedge \forall z{\le}c.\neg\theta(z,\sigma)$を満たす$c$がある。よって、$\vdash \theta(y,\sigma)\to c{\lt}y$。$\vdash \theta(y,\sigma)\to \exists z{\le}y(\theta(z.\neg\sigma))$、即ち $\vdash \neg\Theta(\sigma)$。
※$\neg\Theta(\sigma)$は$\Pi_1$命題だから、$\vDash\neg\Theta(\sigma)$から $\vdash\neg\Theta(\sigma)$は言えない。
定理．$\Theta(x)$のゲーデル文$G_\Theta$に対し、$\not\vdash G_\Theta$ かつ $\not\vdash \neg G_\Theta$ かつ $G_\Theta\circeq \top$。
証明. $G_\Theta{\equiv}\psi_\Theta(\psi_\Theta){\equiv} \forall y(y=\psi_\Theta{\to} \neg\Theta(y(\psi_\Theta)))$と書けるから、$\vdash \neg G_\Theta$なら上の補題より$\vdash \neg\Theta(G_\Theta){\equiv}\neg\Theta(\psi_\Theta(\psi_\Theta))$。よって$\vdash G_\Theta$となり、矛盾。
$\vdash G_\Theta$なら、$\Pi_1$命題$G_\Theta{\circeq}\neg\Theta(G_\Theta){\equiv} \forall y(\theta(y,G_\Theta){\to}\exists z{\le}y(\theta(z,\neg G_\Theta))){\circeq}\top$で、$\theta(a,G_\Theta)$を満たす$a$に対し$\exists z{\le}a(\theta(z,\neg G_\Theta))$より$\vdash \neg G_\Theta$。これも矛盾。
$\not\vdash G_\Theta$より $\top {\circeq} \forall y(\neg\theta(y,G_\Theta)) {\circeq} \forall y(\theta(y,G_\Theta){\to}\exists z{\le}y(\theta(z,\neg G_\Theta))){\equiv}\neg\Theta(G_\Theta) {\circeq} G_\Theta$
第二不完全性定理
$\vdash$において、無矛盾性を示す命題を$\mathcal{C}{:\equiv}\forall y\neg\theta(y, \neg0{\le}0)$とおき、論理式$\varphi(x)$に対する数学的帰納法を表す命題を$\mathcal{I}_\varphi{:\equiv}(\varphi(0){\wedge}\forall x(\varphi(x){\to}\varphi(x{+}1))){\to}\forall x\varphi(x)$とおく。
定理．任意の$\Sigma_1$式$\varphi(x)$に対し$\vdash \mathcal{I }_\varphi$、ならば$\not\vdash \mathcal{C}$
略証．$\vdash \mathcal{C}$と仮定して矛盾を導く。$\vdash$では$\Sigma_1$式に対する数学的帰納法が使えるので、第一不完全性定理にいたる証明を$\vdash$の中で展開できて①、$\vdash \forall y(\neg\theta(y,G_\Theta))$、$\vdash \forall y(\neg\theta(y,\neg G_\Theta))$、$\vdash G_\Theta$②が成立つ。$\vdash G_\Theta$なら $\vdash \exists y\theta(G_\Theta)$だから、矛盾。
①$\Sigma_1$命題$\varphi$に対し、$\varphi \drarrow {}\vdash\varphi$の証明を$\vdash$で展開し、$\vdash \varphi {\to} \exists y\theta(y,\varphi)$ を導出するために、$\Sigma_1$式に対する数学的帰納法の仮定が必要になる。
②$G_\Theta{\circeq}\top$の証明を$\vdash$で展開すれば $\vdash G_\Theta$が示せる。