言語理論とオートマトン：第８章　計算量の理論　　 0章 1章 2章 3章 4章 5章 6章 7章

この章の概要

一般論に入る前に、べき乗計算と整列(大きさの順に並べる)について、具体的に計算時間を測定してみる。
・計算量の概念について理解する
・$\mathcal{P}$、$\mathcal{NP}$の定義を理解し、$\mathcal{P}\ne\mathcal{NP}$問題の意味を知る
・公開鍵暗号系の仕組みを理解する
・マジックプロトコルについて知る

ベキ乗$y^x$の計算時間

　ベキ乗$y^x$の計算は、計算手法(アルゴリズム)の巧拙によって、極端に計算時間が異なる。

 z=y;【zにyのx乗が求まる】
 x>1 の間以下を繰返す
   z=z*y; x=x-1;
素朴なベキ乗計算法
　$y,y^2,y^3,\cdots,y^x$と$y$を順に掛けていくと、$y^x$を計算するのに$x-1$回の掛け算が必要で、ほぼ$x$に比例する計算時間がかかる。この方法(右のプログラム)の計算時間は、$x$の桁数(表示サイズ)の指数乗かかり、桁数が増えると現実的ではない。

 z=1;【zにyのx乗が求まる】
 x>0 の間以下を繰返す
   xが奇数なら z=z*y;
   y=y*y; x=x÷2;
高速ベキ乗計算　Binary法
　例えば、$y^{22}=y^{16+4+2}=y^{16}y^4y^2$を利用すると、$y^2,y^4,y^8,y^{16}$の計算に必要な乗算4回と合わせて$y^{22}$が乗算6回で計算できる。
　この方法(右のプログラム)では、$x$が2進表示で$k$桁のとき、$y^1,y^2,y^4,\cdots,y^{2^{k-1}}$の系列を計算するのに乗算$k{-}1$回、これらを組み合わせて$y^x$を計算するのに(最大)$k{-}1$回の乗算、計$2(k{-}1)$回の乗算で$y^x$を計算できる。2進10桁はほぼ10進3桁($2^{10}=1024\fallingdotseq 10^3$)なので、高速ベキ乗は$x$の10進桁数$\log_{10} x$に比例する(約$20/3$倍)時間(乗算回数)で計算できる。

実験．$y^x \bmod m$の計算時間をMOD電卓で試してみよう
【yx】ボタンは1に$y$を$x$回掛けて$y^x$を計算
【速yx】ボタンは高速ベキ乗計算
１．上の電卓で計算時間を実測して次の表を埋め、【yx】はほぼ$x$に比例する時間がかかることを確かめよ。黄色の欄は、実測してはいけない！他の実測値から計算時間の概算値を予測せよ。
　yx $6^{100,000,000}$ $6^{200,000,000}$ $6^{1,000,000,000}$ $6^{1,000,000,000,000}$
【yx】
【速yx】
（注．速すぎて測定できない場合、計算時間が0msとでる）
２．【速yx】で$6^{1,000,000,000,000}$ の計算に必要な乗算回数の概数を求めよ。

　実験からも明らかなように、計算時間の実測値は(その時の実行環境によって)都度異なるので、プログラムの解析で求めた式に概ね従うにすぎない。それでも、計算時間の増え方の式から、黄色の欄の予測値の計算ができる。

整列(ソーティング)

データを大きさの順に並べ替える整列には多くの手法が知られている。以下のアプリでは【生成】したデータ数が、20以下であれば整列法のデモが見られ、20より大なら計算時間だけが確認できる。基数ソート以外のどの手法も、計算時間は表示された赤字の数(データの大小比較の回数)に比例する。


選択ソート
「未整列部(赤字)の最大値を選択して右端に移動させる(青字)」ことを繰り返す。データ数$n$に対し、計算時間は常に$n(n+1)/2$に比例する。

クイックソート
「未整列部([赤字])を、右端の値を基準に、それ以下([赤字])とそれ以上([赤字])に分割」を繰り返す。平均計算時間は$n\log n$（計算例で赤字部分の長さの総和）に比例する。

挿入ソート
「未整列部(黒字)の最右データを整列部の正しい位置(緑字部の左)に挿入する」ことを繰返す。計算時間(赤字部分の長さの総和)は最悪$n(n+1)/2$に比例し、最良の場合$n$に比例する。

　他の整列法、マージソート・基数ソートの説明は省略する。
実験．整列法比較アプリ
１．選択、クイック、挿入、各ソートのデモで、計算法を確認せよ。
２．デモで整列した後のデータに対し、クイックソート、挿入ソートがどのように動くか確認せよ。
３．整列法比較アプリで空欄の計算時間を実測し、上に示した見積りに概ね従うことを確認せよ。黄色の欄は実測せずに他の欄の値から推測せよ。
データ数 10000 20000 30000 1000000 2000000 3000000 10000000
選択
クイック ーー ーー ーー
挿入
４．クイックソートでは最悪の場合、選択ソートに比例する時間がかかる。それはどのような場合か。
５．挿入法で最良の計算時間になるデータは、どのようなデータか。

実験でも確かめられるように
１．データによって計算時間の増加傾向は異なる。そのため通常は最悪計算時間または平均計算時間が問題にされる
２．一般に選択ソートより挿入ソートの方が速いが、それらは同じ増加傾向($n^2$に比例)を示す

プログラムの計算量

　問題(入力データ集合)$\mathcal{D}$を解くTM(プログラム)$M$が、入力データ$D\in\mathcal{D}$の計算(認識)に必要なテープ長(メモリ)を$S(D)$、ステップ数(時間)$T(D)$とおき、長さ(サイズ)$n$のデータの集合を$\mathcal{D}_n:=\{D\in\mathcal{D}\mid |D|=n\}$とおく。
$S_\max(n):=\max\{S(D)\mid D\in\mathcal{D}_n\},\ \left(S_{\rm avg}(n):=\sum_{D\in\mathcal{D}_n}S(D)/|\mathcal{D}_n|\right)$ $T_\max(n):=\max\{T(D)\mid D\in\mathcal{D}_n\},\ \left(T_{\rm avg}(n):=\sum_{D\in\mathcal{D}_n}T(D)/|\mathcal{D}_n|\right)$
を各々$M$の最悪(平均)領域計算量、最悪(平均)時間計算量という。

例．線形有界オートマトンは$S_\max(n)\leqq kn$のTMである。

　以下、特に最悪・平均を区別せず主に$M$の時間計算量(単に$T(n)$と表す)を扱い、実験で行ったような$T(n)$の漸近的な増え方を問題にするために、オーダーの概念を導入する。①「ある$n_0$と$c$が存在して$n>n_0\to f(n)\le cg(n)$」が成立つ時$f(n)\precsim g(n)$と書いて、$f(n)$はオーダー$g(n)$であるという。例えば$f(n)\precsim n{\cdot}f(n)$であるが、通常$g(n)$は条件①を満たす関数の中で、より小さくより簡単な関数を選ぶ。【$f(n)=O(g(n))$と書く慣習は誤謬の素になる】

例．$f(n)$がいくつかの項の和で表されるとき、増え方が最大の項で係数を1に置き換えたものを$g(n)$とすれば$f(n)\precsim g(n)$。例えば、$5n^2+3n+2\precsim n^2$、$2^n+100n^{10}\precsim 2^n$。$n!+10^n\precsim n!$ である。

このように、オーダーを問題とする立場からすれば、時間計算量$T(n)$を求める際、実行されるすべての命令を数える必要はなく、べき乗や整列の例題で議論したように、適切な演算を定めてその回数を数えればよい。実際、 べき乗では乗算の回数を数え、整列では赤字(データの大小比較)の個数を基に計算時間を議論している。

主な関数の値とサイズ10のデータを単位(1ms)とした時の計算時間の表
（ms:ミリ秒、s:秒、m:分）
$n$$1$$2$$4$$8$$10$$100$$1000$$10000$
$1$ms$10$ms$0.1$s$1$s
$n^2$$1$$4$$16$$64$$100$$10^4$$10^6$$10^8$
$1$ms$0.1$s$10$s$16$m$40$s
$\log_2 n$$0$$1$$2$$3$$3.322$$6.644$$9.966$$13.288$
$1$ms$2$ms$3$ms$4$ms
$n\log_2 n$$0$$2$$8$$24$$33.22$$664.4$$9966$$132877$
$1$ms$20$ms$0.3$s$4$s
$2^n$$2$$4$$16$$256$$1024$$1.268{\times}10^{30}$$1.072{\times}10^{301}$$1.995{\times}10^{3010}$
$1$ms$3.9{\times}10^{16}$年
　上の表で注目すべきは$2^n$(指数関数)の値の増え方である。素朴べき乗のように、時間計算量がオーダー$2^n$の時、サイズ$10$の問題を$1$msで解けたとしてもサイズ$100$の問題を現実的な時間内に解くことはできない($3.9$京年！かかる)。

手に負えない問題
　上の議論を踏まえて、：最悪計算時間が問題(入力)のサイズの多項式で抑えられるプログラムを実行可能であるという。すなわち、高速べき乗プログラムや整列プログラムはどれも実行可能であるが、素朴べき乗プログラムは実行可能ではない。
　そして、実行可能なプログラムが存在しない(する)問題を手におえない(負える)問題という。したがって、べき乗や整列問題はどちらも手に負える。一方、非決定性有限オートマトンを決定性オートマトンに変換する問題は出力の長さ(DFAの状態数)が入力の長さ(NFAの状態数)の指数関数倍になる例があるので、手に負えない。さらに、与えらえたプログラムが与えれれた入力に対して停止するかという問題も、計算可能でさえなく、手に負えない。
　以後、問題をいくらでも大きなサイズの問題例がある判定(yes/no)問題に限定する。

パズル．多項式時間プログラムを実行可能なプログラムと言うことの是非を論ぜよ。

グラフのオイラー路とハミルトン路

ここで、２つのパズルを考えてみよう。

パズル1．ケーニヒスベルグの7つの橋
　右図の橋を一度ずつ通る散歩路はあるか。言い換えると、最右図のグラフは一筆書きできるか。

Wikipedia

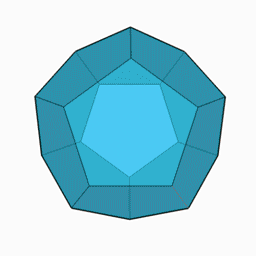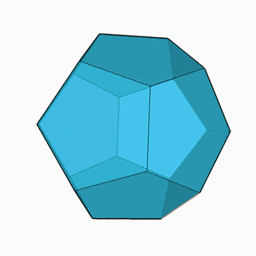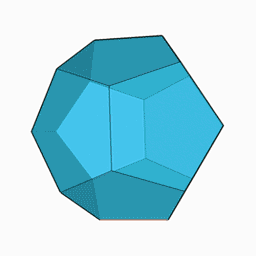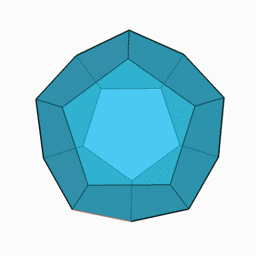
パズル2．ハミルトンの世界一周パズル
　正12面体(右図)の各頂点を1度ずつ通る周遊路はあるか。言い換えると最右図のグラフの各頂点を1度ずつ通って元に戻る路はあるか。

(無向)グラフ$G$は直感的には頂点（○）とそれを結ぶ辺（―）からなる図形である。形式的には$G=(V,E,\gamma)$で、頂点の有限集合$V$、辺の有限集合$E$、端点割当$\gamma:E\to \ddot{V},\ \ddot{V}:=\{\{u,v\}\mid u,v\in V\}$からなる。$\gamma(e)=\{u,v\}=\{v,u\}$の時$e$は$u$と$v$を結ぶ辺であり、特に$\gamma(e)=\{u,u\}=\{u\}$の時、$e$は$u$から$u$へのループ辺である。

　右上図はケーニヒスベルグの橋のグラフ $G{=}(\{0,1,2,3\},\{a,b,c,d,e,f,g\},\gamma)$ で、$\gamma(a){=}\{0,1\},$$\gamma(b){=}\{0,2\},\gamma(c){=}\{0,3\},\gamma(d){=}\gamma(e){=}\{1,2\},\gamma(f){=}\gamma(g){=}\{1,3\}$である。グラフでは頂点と辺の接続が問題で、図示の際の頂点や辺の位置は分かりやすいように描けばよい(【再描画】してみよ)。

　$G$の路とは、辺の列$\vect{e}=e_1e_2\cdots e_n\in E^*$で、頂点列$v_0v_1\cdots v_n$に対し$\gamma(e_i)=\{v_{i-1},v_i\},\ i=1,2,\dots,n$が成立つものをいい、$v_0, v_n$を路$\vect{e}$の端点という。特に$v_0=v_n$の路$\vect{e}$を閉路といい、空列$\varepsilon$は任意の頂点$v$を端点とする閉路である。また、グラフは任意の2頂点の間に路がある時連結であるという。
　連結グラフ$G$に対し、
  • 各辺　を1度ずつ通る(閉)路をオイラー(閉)路といい、
  • 各頂点を1度ずつ通る(閉)路をハミルトン(閉)路という。
上述のパズルは、与えられたグラフに、1.オイラー(閉)路はあるか、2.ハミルトン(閉)路はあるか。を問う問題である。実はこれらは、次の定理により、計算量的に似て非なる問題である。
奇数個の辺を持つ頂点を奇頂点といい、グラフ$G$の奇頂点の数を$O(G)$と表す。辺は2つの端点を持つから、$O(G)$は偶数である。

ウィキペディア

オイラーの定理 連結グラフ$G$に対し、
オイラー閉路(路)がある$\iff O(G)=0$($O(G)=0または2$)
証明．$\Longrightarrow)$ オイラー路の辺はグラフの辺全部を1度ずつ使い、端点で1本の辺を、中間頂点で2本(入りと出)の辺を使う。この事から、$O(G)=0$の時$G$のオイラー路は閉路であり任意の頂点から始められる。一方、$O(G)=2$のとき$G$のオイラー路は奇頂点から始まる。
$\Longleftarrow)$ $G=(V,E,\gamma)$の辺の数$n$に関する帰納法。$n{=}0$なら明らか。$u$を奇頂点(なければ任意の頂点)とし、$\gamma(e){=}\{u,v\},\ G'=(V,E-\{e\},\gamma)$とする。$u$の選び方から$O(G'){=}0,2$で$O(G')=2$なら$v$は$G'$の奇頂点である。よって、$G'$が連結なら$v$から始まる$G'$のオイラー路を$e$の後に続けた路は$G$のオイラー路である。$G'$が$u$を含む連結グラフ$G_1$と$v$を含む連結グラフ$G_2$に分かれるなら、$O(G_1)=0$である。よって、$u$で終わる$G_1$のオイラー閉路に$e$と$v$から始まる$G_2$のオイラー路を順につなげれば$G$のオイラー路になる。なおこの証明は、グラフ$G$のオイラー路を具体的に求める再帰的な手順を示している。

　与えられたグラフにオイラー路があるかという問題は、オイラーの定理より各頂点の辺の数を数えるだけで解け、手に負える問題である。
　一方、ハミルトン路の解法にはオイラー路のような簡明な判定法がなく虱潰しの試行錯誤しかないので、頂点数の階乗時間かかる手に負えない問題であると信じられている。どうしてそんなことが言えるのか、「信じられている」とはどういう意味か、そのカギを握るのが次節で述べる非決定性プログラム(TM)である。

非決定性プログラム

　これまでに、決定性TMが非決定性TMを模倣できることや、プログラムは(決定性)TMを模倣できること、したがってTMとプログラムは理論的に同等の認識能力を持つこと等を示した。プログラムは本質的に、コンピュータで翻訳・実行されるものであるから、決定性でなければならないが、ここで理論的なモデルとして非決定性プログラム(非決定性TMのプログラム版)と考えてみよう。

　動作を有限個の候補の中から選べる命令を非決定性命令といい、非決定性命令を含むプログラムを非決定性プログラムという。非決定性プログラムは、次の動作をうまく選んだ時に正しく計算できればよい、すなわち、可能な計算の中に正しく計算するものがあればよい、と考える。このことは、判定問題(答えがyes/noの問題)に対し、正答がnoのときにyesと答えるような計算列があってはいけないことを意味する。
　計算時間は正しく計算するものの中での最短時間と考えるので、次の表のようにまとめることができる。
非決定性判定問題プログラムの計算時間
正答出力yesの場合出力noの場合計算時間
yesありあってもよい出力yesの最短時間
noなしあってもよい除外してよい

時間限定(非決定性)プログラム
　上の表で「答がnoの場合の計算時間は除外」ということを理解するために、時間限定プログラムという概念を導入しよう。(非決定性)プログラム$P$が$t(n)$時間限定であるとは、サイズ$n$のすべての入力の(すべての)計算に対し必ず$t(n)$時間(基本命令の$t(n)$ステップ)以内に停止することをいう。決定性プログラム$P$の時間計算量が$T(n)$であることと、$P$が$T(n)$時間限定であることとは同値である。
　(表の意味で)時間計算量$T(n)$の(非決定性)プログラム$P$に対し、入力サイズ$n$と時間を測って、$t(n)$時間で強制的に停止させ(その時点でyesの出力でなければ)noと答えるようにした$t(n)$時間限定プログラムを$P_{t(n)}$とおく。$T(n)>t(n)$となる$n$があれば$P\ne P_{t(n)}$であるが、$T(n)\le t(n)$であれば$P=P_{t(n)}$である。すなわち判定問題が、表の意味で$T(n)$時間プログラムで計算できることと、$T(n)$時間限定プログラムで計算できることとは同値である。以後、$T(n)$時間限定の表記を用いる。

定理．$T(n)$時間限定非決定性プログラムで計算できる判定問題は、$a^{T(n)}$時間限定決定性プログラム($a$は選択肢数の最大値)で計算できる。
略証：NTMのDTMによる模倣同様、高々T(n)時間以内のすべての計算（選択肢）を虱潰しで調べればよい。

$\mathcal{P,\ NP}$

　時間限定の概念をTMにも適用する。DTM(NTM)は、長さ$n$の任意の入力の(任意の)時点表示列が長さ$t(n)$以内であるとき、$t(n)$時間限定であるという。

　$T(n)$が$n$の多項式であるとき、$T(n)$時間限定を多項式時間限定という。
・多項式時間限定決定性プログラム(DTM)で解ける判定問題のクラスを$\mathcal{P}$、
・多項式時間限定非決定性プログラム(NTM)で解ける判定問題のクラスを$\mathcal{NP}$
で表す。

問．$\mathcal{P},\mathcal{NP}$の上の定義はプログラムでもTMでも同じクラスを定義することを示せ。ヒント．ある多項式$s(n)$が存在して、$t(n)$限定プログラム(TM)を模倣する$s(t(n)$限定TM(プログラム)が存在することを示せ。

　明らかに$\mathcal{P}\subseteq\mathcal{NP}$である。しかし、$\mathcal{P}\ne\mathcal{NP}$か否かは有名な未解決問題 (ミレニアム問題)である。

例．グラフのオイラー・ハミルトン路存在判定問題には、大きな違いがある。
1. オイラー路：オイラーの定理があり、$\mathcal{P}$に属す
2．ハミルトン路：路を非決定的に生成しハミルトン路であるかチェックするプログラムは多項式時間限定非決定性プログアムなので$\mathcal{NP}$に属すが、$\mathcal{P}$に属すか否かは未解決である。

$\mathcal{NP}$問題の別表現
証拠が与えられれば、その答えがYesであることを、問題(入力)サイズの多項式時間内に検証できる問題 （注意：証拠のサイズではない！）

パズル．１．$\mathcal{NP}$は何の略か。
２．上の注意にあるが、証拠のサイズでよければ停止問題は$\mathcal{NP}$であることを示せ。

$\mathcal{NP}$完全問題

$\mathcal{NP}$問題$P$を解く任意のプログラム$M_P$から、すべての$\mathcal{NP}$問題$Q$に対して、$Q$を解くプログラム$M_Q$を多項式時間で作れるとき、$P$は$\mathcal{NP}$完全であるという。

$\mathcal{NP}$完全問題のどれか１つでも$\mathcal{P}$問題であれば、$\mathcal{P}=\mathcal{NP}$である。つまり、$\mathcal{NP}$問題の中で、もっとも難しいと考えられる問題、と考えられる。

Cookは充足可能性判定問題が$\mathcal{NP}$完全であることを示した(1971)。

充足可能性判定問題
与えられた論理式の値を真にする変数値の割り当てが存在するか否か判定する問題

パズル．$\mathcal{P}=\mathcal{NP}$であれば、どのようなことが言えるか。

証明のアイディア 　$M_P$：$\mathcal{NP}$問題$P$を解く非決定性多項式$p(n)$時間チューリング機械
　$M_P$はサイズ$n$の入力$x$に対し、$N-1:=p(n)$ステップで問題$P$の答$P(x)=$yes/noを(例えば)最初のセルに書き込んで停止する
$M_P$の入力$x$に対する動作列を記述し答がyesかnoかを判定する論理式$L(x)$を$N$の多項式時間で作り、$L(x)$が充足可能⇔$P(x)=$yes となるようにする
変数=真 の意味個数
$S_{tq}$時点$t$の$M_P$の内部状態が$q$$N$×状態数
$T_{tka}$時点$t$のテープセル$k$の内容が記号$a$$N^2$×記号数
$H_{tk}$時点$t$のヘッド位置が$k$$N^2$
これらの変数に対する真偽の割り当てが、$M_P$の正しい計算になって(動作規則を満たして)いて出力がyesのときにのみ真となるような論理式をつくればよい。

$\mathcal{NP}$完全問題の例 充足性判定問題
ハミルトン(閉)路問題：与えれれたグラフがハミルトン(閉)路を持つか
巡回セールスマン問題：与えれた都市をすべてめぐるコスト$w$以下の路があるか
3彩色問題：与えれたグラフの頂点を3色で塗り分けることができるか
　（すべての平面グラフは4彩色可能であることが知られている）

$\mathcal{P}$問題ではなさそうな$\mathcal{NP}$問題
素因数分解：与えられた数の素因数分解を求める
（素数判定は最近(2002年)$\mathcal{P}$問題であることが示された）

公開鍵暗号

送信者　　　　 通信路　　受信者
平文[暗号化]⇒　暗号　⇒[復号]平文　

共通鍵暗号：送信者と受信者で実質的に同じ鍵を用いる
　鍵(と手順)を秘密裡に共有し(ネット上で可能？)
　送られた暗号をその鍵で復号
　例 IBM[1文字前]⇒ HAL ⇒[1文字後]IBM

公開鍵暗号：送信者(暗号化)と受信者(復号)で異なる鍵
　受信者が暗号化の鍵(と手順)を公開
　送られた暗号を秘密にしている鍵で復号
　公開(暗号化)鍵から秘密(復号)鍵が分からないのか？
　　　RSA暗号、楕円曲線暗号

パズル．通信路の盗聴者が、公開鍵暗号を破るための方法を考えよ。

RSA公開鍵暗号の作成実験

$\equiv_n$：法$n$で（$n$で割った余りが）等しい
$p,q$が素数のとき
$x\equiv_{pq}x^{1+(p-1)(q-1)}\equiv_{pq}x^{1+2(p-1)(q-1)}\equiv_{pq}\cdots$より
$de\equiv_{(p-1)(q-1)}1\Rightarrow(x^d)^e=(x^e)^d=x^{de}\equiv_{pq}x$

$n=pq$を法(mod)として$d$乗と$e$乗が互いに逆関数⇒暗号化と復号に利用

パズル．上のアプリと右のmod電卓を使って以下を確かめよ
  1. 「暗号送信」と「複号」がうまく働く
  2. 実験で使った $e,p,q$ から、$d:=1÷e \mod(p-1)(q-1)$で$d$が求まる
  3. 実験で使った $e,d,n$ に対し、適当な$x$で$(x^d)^e\equiv_n(x^e)^d\equiv_nx$となる

RSA暗号の安全性

RSA暗号を破る（考えうる）方法：公開鍵$(e,n)$は既知
  1. 暗号(の値)を、法$n$で1乗、2乗、3乗、…して元に戻るか否かを調べる。$d$乗で元に戻るから、秘密鍵$d$をいつかは知ることができる
  2. $n$の素因数分解で$p,q$を求め、法$(p-1)(q-1)$で$1÷e$を計算して$d$を求める
  3. 平文(の一部)$x$を推測し、法$n$で$e$乗して盗聴暗号(の一部)$y$と一致するか見る
注．前頁の実験は簡単のため換字暗号になっており、3.に対しては安全でない。

すべて虱潰しの方法であり、素朴ベキ乗計算の実習でみたように、$n$の値や秘密鍵$e$、素数$p,q$を十分おおきくすれば安全と考えてよい。
　ところで、$x^d$の計算は復号計算でもあるから、その計算に$x$を$d-1$回掛ける素朴な方法しかなければ、復号にとんでもない時間がかかってしまい、RSA暗号は機能しない。幸い、$d$の値がわかっていれば、$d$乗はBinary法で高速計算できる

暗号の安全性と$\mathcal{P}\ne\mathcal{NP}$

　以上のことから、復号は、秘密鍵$d$を知っている本人は高速実行できるが、たとえ暗号を入手(盗聴)できたとしても、秘密鍵を知らない第3者が可能な素朴な方法では、現実的な時間内に実行できない ことがわかる。
　現在のところRSA暗号を現実的な時間内に破る方法は知られていない。
１．について言えば、与えられた $x,y,n$に対し、$x=_ny^d$を満たす$d$を求める効率的な方法は知られていないし、
２．についていえば、$n$から$p,q$を求める効率的な因数分解の方法は知られていない。

　しかし、何か巧妙な方法が、まだ見つかっていないだけで、今後見つかる可能性が0とは今のところわかっていない。そのような方法は存在しえず、それゆえRSA暗号は安全であると広く信じられてはいるが、そのことの数学的に厳密な証明は得られていない。
　このことは、$\mathcal{P}\ne\mathcal{NP}$問題というクレイ数学研究所から100万ドルの賞金がかけられている有名な未解決問題の一つに関わる問題である。

電子署名

署名＝文書を秘密鍵で暗号化したもの
文書＋署名の受取人は公開鍵で署名を復号して文書との一致を検証する

公開鍵で復号できる暗号(＝署名)を作れるのは秘密鍵の持ち主だけ
⇒文書の改ざん、署名の偽造(なりすまし)が防げる

パズル．右上のアプリを使って、以下のことを確かめよ
  1. 「署名付き送信」と「署名検証」がうまく働く
  2. 「署名検証」は文書の改竄を発見できる
  3. 「署名検証」は署名の偽造を発見できる

署名者は、秘密(鍵)を明かさずに本人（秘密(鍵)の持ち主）であることを証明
⇔ゼロ知識証明

マジックプロトロコル

コイントス：A,B 両者が信頼できる第三者を介さずに通信線上で行う
　・AはBに投げたコインの情報を送信し（以後Aはコインの裏表を変えられない）
　・Bは裏表を当てる（Bが得た「情報」からはコインの裏表が分からない）
　・Bが答えた後、その当否を両者(特にB)が確認できる
ことを実現する
コイントスプロトコル(通信手順)：Aの公開鍵を利用
  1. Aは乱数 $r$ をBに送り、$r$ のAによる署名の偶奇をBに問う
  2. Bは偶奇を答える
  3. Aは $r$ の署名をBに送り、Bは(Aの公開鍵で)それを検証する

パズル．上のプロトコルがうまく働くことを示せ

他のマジックプロトコル：いずれも通信線上で第三者を介さずに行う
金持ち比べ：互いの資産額を知らせずに、その大小を比べる
カード配り：トランプのカードを配る
電子投票：投票の秘密を保って投・開票を行う
参考：情報セキュリティの科学