この章の目標
本書で主に扱う対象は文字列の集合ですが、本章は、その準備の章です。最初に、本書全体を通して陰に陽に使われる、集合と論理に対する基本的な記法や概念について紹介します。また、本書を通じて、色々な場面にいろいろな形で現れるグラフの概念や(数学的)帰納法についても紹介します。さらに、発展的な話題として、予備知識として有効ないくつかのトピック、自然数上の加算を含む論理式で表わされる集合や、集合の濃度、集合の定義に潜むパラドックス、アリストテレスの名辞論理、についても概説します。
集合と論理の記法
集合は、素朴には要素(の表現)の集まりで、要素$a$が集合$A$に属す($a{\color{blue}\in} A$)か否かが明確に定まる❶ものである。集合の表現には要素を列挙する外延的記法と、要素が集合に属す条件を記述する内包的記法がある。
外延的記法:$\{2,3,5,7\}$
内包的記法:$\{x\mid xは10以下の素数\}$
内包的記法では、要素を表す変数、例えば$x$を用いて、$\{x\mid xの述語\}$という形で記述する。ここで「$x$の述語」は、要素がその述語を満たすか否かを明確に定めるもので、この意味で集合と1変数述語とは密接に対応する❶。内包的記法:$\{x\mid xは10以下の素数\}$
外延的記法では、誤解が生じない限り$\{2,4,6,\dots\}$のように$\cdots$を用いてもよい。また、要素の順番や重複❷は無視され、例えば$\{2,3,5,7\}=\{5,2,3,7,2\}$である。
❶ 厳密には問題があるが、これについては後で議論する。
❷ 要素とその表現の関係には、注意が必要である。
数の集合としては$\{2\}=\{2,1{+}1\}$【$1{+}1$は$2$の別表現】だが、
数式の集合としては$\{2\}\ne\{2,1{+}1\}$【$2$と$1{+}1$は異なる式】である。
上の❷でも触れているが、集合を定義するときには、考えている世界が何かが重要で、その世界の全要素の集合を全体集合といい、通常$U$で表す。
集合と論理
以下、あいまいさを避け簡潔に表現するために、"$P$または$Q$"を$P\vee Q$、"$P$かつ$Q$"を$P\wedge Q$、"$P$でない"を$\neg P$、"$P$ならば$Q$"を$P\drarrow Q$❸と表す。$P,\,Q$が同値($P\drarrow Q\wedge Q\drarrow P$)の時$P\rlarrow Q$と表し、$P\drarrow Q\wedge Q\not\drarrow P$を$P\darrow{\rightarrow}{\not\leftarrow}Q$と表す。
❸ 本講では記号$\rightarrow,\Rightarrow$を別の意味に用いる。
集合$A$とそれを内包的に表す述語$\mathcal{A}(x)$とはその内包的表現を介して密接に対応し、$A:=\{x\mid \mathcal{A}(x)\},\, B:=\{x\mid \mathcal{B}(x)\}$とすれば、
$\mathcal{A}(x)\darrow{\rightarrow}{\leftarrow}\mathcal{B}(x)$の時、$A$と$B$は等しい($A{\color{blue}=} B$)といい、
$\mathcal{A}(x)\drarrow\mathcal{B}(x)$の時、$A$は$B$に含まれる($A{\color{blue}\subseteq} B$)といい、
$\mathcal{A}(x)\darrow{\rightarrow}{\not\leftarrow}\mathcal{B}(x)$の時、$A$は$B$に真に含まれる($A{\color{blue}\subset}B$)という。
|
|
|
|
|
|
| ウィキペディア |
和集合:$A{\color{blue}\cup}B:=\{x\mid \mathcal{A}(x)\vee \mathcal{B}(x)\}$(右上図)
積集合:$A{\color{blue}\cap}B:=\{x\mid \mathcal{A}(x)\wedge \mathcal{B}(x)\}$(右中図)
差集合:$A{\color{blue}\setminus}B:=\{x\mid \mathcal{A}(x)\wedge \neg\mathcal{B}(x)\}$(右下図)
補集合:$A^{\color{blue}\complement}:=U\setminus A=\{x\mid \neg\mathcal{A}(x)\}$
全体集合$U$を定めないと補集合の範囲が不明確になる。
直和:$A{\color{blue}{\,\dot\cup}\,}B:=\{x\mid \mathcal{A}(x)\vee \mathcal{B}(x)\}$。ただし、
$A \,\dot\cup\, B$と書けば、暗黙裡に$A\cap B=\emptyset$と仮定する。
冪集合:$\mathbb{2}^A:=\{B\mid B\subseteq A\}$❶
集合$A$は含まれる要素の数が有限の時有限集合といい、その要素数を$|A|$と表す。非有限集合を無限集合という。
問.1. 上にならって補集合を図示せよ
2. $\mathbb{2}^{\{a,b,c\}}$を求めよ。
3. $|A|=n$ならば$|\mathbb{2}^A|=2^{n}$であることを示せ。
集合$A$に対しその特徴関数$\pmb{[}A\pmb{]}:U\to \{0,1\}$を$a{\in}A\rightleftarrows \pmb{[}A\pmb{]}(a)=1$で定義すれば、$A$と$\pmb{[}A\pmb{]}$は1対1に対応する。
問.$\pmb{[}A^\complement\pmb{]}(x)=1-\pmb{[}A\pmb{]}(x)$である。$\pmb{[}A{\cap}B\pmb{]}(x),$ $\pmb{[}A{\cup}B\pmb{]}(x),$ $\pmb{[}A{\setminus}B\pmb{]}(x),$ $\pmb{[}A{\dot\cup}B\pmb{]}(x)$を$\pmb{[}A\pmb{]}(x),\pmb{[}B\pmb{]}(x)$を用いて表せ。
❶ $A$の冪集合$\mathbb{2}^A$は、部分集合を$A$から$\mathbb{2}{:=}\{0,1\}$への(特徴)関数と見做した表現である。一般に、写像$f:A\to B$の集合を$B^A$と表す。
ドモルガンの法則$(A\cup B)^\complement=A^\complement\cap B^\complement$を証明してみよう。
1. 特徴関数を使えば、以下のように計算できる。
$\pmb{[}(A{\cup}B)^\complement\pmb{]}(x)=1-\pmb{[}A{\cup}B\pmb{]}(x) =1-(\pmb{[}A\pmb{]}(x)+\pmb{[}B\pmb{]}(x)-\pmb{[}A\pmb{]}(x)\pmb{[}B\pmb{]}(x))$
$=(1-\pmb{[}A\pmb{]}(x))(1-\pmb{[}A\pmb{]}(x))=\pmb{[}A^\complement\pmb{]}(x)\pmb{[}B^\complement\pmb{]}(x)=\pmb{[}A^\complement{\cap}B^\complement\pmb{]}(x)$
2. 内包的表記では $(A{\cup}B)^\complement{=}\{x\mid \neg(\mathcal{A}(x){\vee}\mathcal{B}(x))\}{=}\{x\mid \neg\mathcal{A}(x){\wedge}\neg\mathcal{B}(x)\}{=}A^\complement{\cap}B^\complement$ と書ける。即ち、論理の式と集合の式の間で一方から他方が導ける。
問.$(A{\cap}B)^\complement=A^\complement{\cup}B^\complement$を示せ。
量化子
例えば$A\subseteq B$を定義した論理式$\mathcal{A}(x)\drarrow \mathcal{B}(x)$は、全体集合を明示して表せば、すべての$x\in U$に対し$\mathcal{A}(x)\drarrow \mathcal{B}(x)$が成立つ、と書ける。これを全称記号$\forall$を用いて $\forall x{\in}U\ \mathcal{A}(x)\drarrow \mathcal{B}(x)$ と表す。$\mathcal{A}(x)\rlarrow \mathcal{B}(x),\ \mathcal{A}(x)\darrow{\rightarrow}{\not\leftarrow} \mathcal{B}(x)$も同様である。
$A=\emptyset$は$\forall x{\in}U\ \neg\mathcal{A}(x)$と表せるが、その否定$A\ne\emptyset$を表す論理式は、ある$x \in U$が存在して$\mathcal{A}(x)$が成立つ、ということなので存在記号$\exists$を用いて$\exists x{\in}U\ \mathcal{A}(x)$となる。即ち、$\exists x{\in}U\ \mathcal{A}(x) \rlarrow \neg(\forall x{\in}U\ \neg\mathcal{A}(x)),\ \forall x{\in}U\ \mathcal{A}(x) \rlarrow \neg(\exists x{\in}U\ \neg\mathcal{A}(x))$が成立つ。これを量化子$\forall,\exists$に対するドモルガンの法則という。
これらの論理記号$\wedge,\vee,\neg,\drarrow,\rlarrow,\forall,\exists$を以後、必要に応じて文中でも利用する。
関係と写像
集合$A$と$B$の直積とは、それらの要素の組の集合$A{\times}B{:=}\{(a,b)\mid a{\in}A, b{\in}B\}$をいい、$A,B$の(2項)関係$R{\subseteq}A{\times}B$に対し、以下を定義する。
- $R^{-1}:=\{(b,a)\mid (a,b){\in}R\} \subseteq B{\times}A$、
- $x{\in}A$に対し、$R(x):=\{y\mid (x,y){\in}R \} \subseteq B,$
- $X{\subseteq}X$に対し、$R(X):=\bigcup_{x\in X}R(x) = \{y\mid \exists x{\in}X((x,y){\in}R)\}$
写像(関数)$f:A{\to}B$のグラフ$\underline{f}:=\{(a,f(a))\mid a{\in}A\}$は、$\forall x{\in}A(|\underline{f}(x)|{=}1)$を満たす関係だから、$\forall x{\in}A(|R(x)|{=}1)$を満たす関係$R{\subseteq}A{\times}B$を写像(関数)といい、$R(a){=}\{b\}$を$R(a){=}b$と表す(単要素集合$\{f(x)\}$をその要素$f(x)$と同一視する)。
問.写像$F$に対し、集合$f^{-1}(x)$の内包的表記を求めよ。
$A$上の2項関係$R,S{\subseteq}A{\times}A$に対し、$RS:=\{(x,z)\mid \exists y\ (x,y){\in}R\wedge (y,z){\in}S\}$と定義し、$R^0{:=}\{(x,x)\mid x{\in}A\},$ $R^{n+1}{:=}R^nR,$ $R^*{:=}\bigcup_{n=0}^\infty R^n$と定義する。$R$は反射的($R^0{\subseteq}R$)かつ推移的($R^2{\subseteq}R$)かつ対称的($R{=}R^{-1}$)の時同値関係であると言い、反射的かつ推移的かつ反対称的($R{\cap}R^{-1}{=}R^0$)の時順序関係であると言う。
問.$R^*{=}R^{-1}\rightleftarrows R$は同値関係、を示せ。
グラフと木
グラフ理論は豊富な内容を持つが、本節では、後の議論で陰に陽に使われる概念と用語のみを紹介する。グラフ (ディズニーの戦略図)
グラフは
例.右図で路aedfの始点は0、終点は3である。
問.右図に、各辺を一度ずつ通る路(オイラー路)は無いことを示せ。
 木
木木(順序木)は、各頂点が根と呼ばれる頂点からの単一の路を持つある種の有向グラフである。各頂点の辺の内、根に近い辺の始点を親、根から離れる辺の終点を子とよび、子には(グラフと異なり)順序がある。子を持たない頂点を葉、葉でない頂点を内点という。
通常(自然界とは逆に)根を上に葉を下にして図示し、子を順序通りに並べる等、頂点の描画位置の自由度はグラフ程にはない。木$t$の根(のラベル)を$\dot{t}$、葉(のラベル)を順に並べた列を$\underline{t}$と表す。
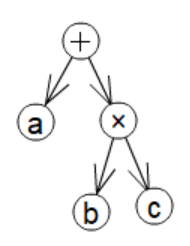
例.木の典型的な例は関数式で、子$x_{1..n}$を持つ頂点$f$を$f(x_{1..n})$と同一視し、2項演算$x\odot y=\odot(x,y)$と見做せば、関数式と木は同一視できる。右上の木$t$は$a{+}b{\times}c=+(a,\times(b,c))$に対応する木であり、$\dot{t}{=}+,\ \underline{t}{=}abc$である。
問.$\sin x-\log_y x$を表す木を求めよ。
帰納(再帰)法
「再帰」は計算機科学における基礎的な概念で、対象の記述(定義・証明・手順)の中で自分自身を利用する事をいう。「帰納」は、論理学の分野で「演繹」に対比して、個々の事例から一般的な命題や法則を導く論法をいうが、自然数に対する再帰的な証明は、その帰納的性格から「数学的帰納法」と呼ばれる。一般に再帰的な記述は帰納的性格を帯びるから、両者を併用して使用する事も多い。本講では「帰納法による証明」以外の文脈では主に「再帰」を用いる。
数学的帰納法
自然数の集合を$\mathbb{N}{=}\{0,1,\dots\}$と表す。例えば$n{\in}\mathbb{N}$に対する$\sum_{i=0}^n i=n(n+1)/2$ の数学的帰納法による証明は
1. $\sum_{i=0}^0 i=0,\ 0(0+1)/2=0$ より$n=0$の時成立つ
2. $n$の時成立つ($\sum_{i=0}^n i=n(n+1)/2$)と仮定すれば、
よって数学的帰納法により任意の$n{\in}\mathbb{N}$に対して与式は成立つ。
という形式をとる。これは、数列$S_n =\sum_{i=0}^n i$と$a_n=n(n+1)/2$は共に同じ漸化式 $S_0:=0,\ S_{n+1}:=S_n+(n+1)$と$a_0:=0,\ a_{n+1}:=a_n+(n+1)$で再帰的に計算できるから等しい、ということに他ならない。
$\mathbb{N}$の再帰的定義
では、漸化式(第0項の定義式と$n$(以下)の項を使った第$n+1$項の定義式)から、すべての$n{\in}\mathbb{N}$に対し数列の第$n$項を定義(計算)できる理由を考えてみよう。それは$\mathbb{N}$が再帰的に
1. $0{\in}\mathbb{N}$。
2. $n{\in}\mathbb{N}$ならば、$(n{+}1){\in}\mathbb{N}$。
3. すべての$n{\in}\mathbb{N}$はこのようにして得られる。
と定義できる(と我々が認めている)からに他ならない。
即ち、$\mathbb{N}$の再帰的定義が数列の再帰的定義(漸化式)とそれに基づく再帰的な証明(数学的帰納法)の正しさを保証する。なお、条件の3.は通常省略されることが多く、本講でも誤解を生じない限り省略する。
別の例として、木を再帰的に定義し、木で成立つ命題を再帰的に証明しよう。
1. 頂点$v$は、$v$が根の木である。(頂点と有向辺は既知とする)
2. 頂点$v$から木$t_{1..n}$の各々の根へ有向辺を引いたものは、$v$が根の木である。
命題.木の頂点数は辺の数$+1$である
証明.木の定義(構成)に関する帰納法で証明する。
1. 1個の頂点のみからなる木では明らかに成立つ。
2. 木$t_{1..n}$で定理が成立てば、合計の頂点数は辺の数$+n$で、それらを$v$の子とする木では、辺が$n$増え頂点が1増えているので定理が成立つ。
問.子の数$n{=}2$の2分木では、葉の数は内点の数$+1$である事を示せ。
再帰的定義と計算
数列の漸化式のような再帰的定義は再帰的手続き(計算法)と密接に結びつく。右は再帰的に $階乗(0)=1,$ $階乗(n)=n\times 階乗(n-1)$ で定義された関数 $階乗(n)$ を計算する再帰的疑似プログラムである。
別の例として、羽田空港から飛行機の乗り継ぎだけで行ける空港の集合$A$の再帰的定義
1.羽田空港${}\in A$、
2.$b$に$a \in A$から直行できる${}\drarrow b\in A$
は右の手順で計算できる。$B$は$A$のうちの未処理空港の集合で、$A$は有限集合なのでこの手順は必ず停止する。
このような、対象の再帰的定義に基づく帰納法による証明や再帰的計算は、今後、様々な場面で出現する。
1. 頂点$v$は、$v$が根の木である。(頂点と有向辺は既知とする)
2. 頂点$v$から木$t_{1..n}$の各々の根へ有向辺を引いたものは、$v$が根の木である。
命題.木の頂点数は辺の数$+1$である
証明.木の定義(構成)に関する帰納法で証明する。
1. 1個の頂点のみからなる木では明らかに成立つ。
2. 木$t_{1..n}$で定理が成立てば、合計の頂点数は辺の数$+n$で、それらを$v$の子とする木では、辺が$n$増え頂点が1増えているので定理が成立つ。
問.子の数$n{=}2$の2分木では、葉の数は内点の数$+1$である事を示せ。
|
function 階乗($n$:自然数) if ($n=0$) 階乗:=1; else 階乗:=$n\times$階乗($n-1$); |
数列の漸化式のような再帰的定義は再帰的手続き(計算法)と密接に結びつく。右は再帰的に $階乗(0)=1,$ $階乗(n)=n\times 階乗(n-1)$ で定義された関数 $階乗(n)$ を計算する再帰的疑似プログラムである。
|
$A:=B:=\{$羽田空港$\};$ 以下を$B\ne\emptyset$の間繰返す $a\in B$ を取り出す $a$ から直行できる各 $b$ に対し if ($b\not\in A$) $A:=A\cup \{b\};$ $B:=B\cup \{b\};$ |
1.羽田空港${}\in A$、
2.$b$に$a \in A$から直行できる${}\drarrow b\in A$
は右の手順で計算できる。$B$は$A$のうちの未処理空港の集合で、$A$は有限集合なのでこの手順は必ず停止する。
このような、対象の再帰的定義に基づく帰納法による証明や再帰的計算は、今後、様々な場面で出現する。
準線形集合とプレスバーガー論理
ここでは発展的な話題を扱い、議論には線型代数の基礎知識が必要である。第$j$成分が$p_j$の$n$次元行ベクトル$\vec{\vect{p}}$を$[p_i]^n$、第$i,j$成分が$p_{ij}$の$m{\times}n$行列を${}_m[p_{ij}]^n,{}_m[\vec{\vect{p}}_i]$等と表し、$\mathbb{N}$上の$n$次元行ベクトル。$m{\times}n$行列の集合を、各々$[\mathbb{N}]^n$、${}_m[\mathbb{N}]^n$と表す。準線形集合
$\vec{\vect{p}}{=}[p_j]^n,\vec{\vect{q}}{=}[q_j]^n \in [\mathbb{N}]^n,\ a{\in}\mathbb{N}$に対し、和$\vec{\vect{p}}{+}\vec{\vect{q}}{:=}[p_j{+}q_j]^n$、定数倍$a\vec{\vect{p}}{:=}[ap_j]^n$、部分順序$\vec{\vect{p}}{\le}\vec{\vect{q}}:\equiv \forall j\, p_j{\le}q_j$、$\vec{\vect{p}}{=}\vec{\vect{q}}:\equiv \vec{\vect{p}}{\le}\vec{\vect{q}}{\wedge}\vec{\vect{q}}{\le}\vec{\vect{p}}$、$\vec{\vect{p}}{\lt}\vec{\vect{q}}:\equiv \vec{\vect{p}}{\le}\vec{\vect{q}}{\wedge}\vec{\vect{q}}{\not\le}\vec{\vect{p}}$と定義する。$\mathbb{N}{}_m[\vec{\vect{p_i}}]{:=}\{[a_i]^m{}_m[\vec{\vect{p}}_i] \mid a_i{\in}\mathbb{N}\}$、$C,P{\subseteq}{}_n[\mathbb{N}]$に対し$C{+}P{:=}\{\vec{\vect{c}}{+}\vec{\vect{p}}\mid \vec{\vect{c}}{\in}C,\vec{\vect{p}}{\in}P\},$ $\mathbb{N}P{:=}\{[a_i]^k{}_k[\vec{\vect{p}}_i] \mid a_i{\in}\mathbb{N}, \vec{\vect{p}}_i{\in}P, k{\ge}0\}$と定義する。$\{\vec{\vect{c}}\}$を単に$\vec{\vect{c}}$と書く。$\vec{\vect{c}}{+}\mathbb{N}{}_m[\vec{\vect{p}}_i]$を線形集合、${}_m[\vec{\vect{p}}_i]$をその周期といい、線形集合の有限和を準線形集合という。
問(準線形集合の例).$x\pmb{|}y:\rightleftarrows \exists z(y{=}zx)$と定義し、$\vec{\vect{e}}_j{:=}[\delta_{ij}]^n,$ $k_{ij}{:=}1{+}(k{-}1)\delta_{ij}$とおく。$i{\in}\mathbb{N}_+$に対し、$\{\vec{\vect{x}}\mid x_i{\gt}0\}{=}\vec{\vect{e}}_i{+}\mathbb{N}{}_n[\vec{\vect{e}}_j],$ $\{\vec{\vect{x}}\mid k\pmb{|}x_i\}{=}\mathbb{N}{}_n[k_{ij}\vec{\vect{e}}_j],$ $\{\vect{x}\mid k {\not\pmb{|}} x_i\}{=}(\bigcup_{l=1}^{k-1}l\vec{\vect{e}}_i){+}\mathbb{N}{}_n[k_{ij}\vec{\vect{e}}_j]$ を示せ。
定理.$S{\subseteq}[\mathbb{N}]^n$に対し$\min(S){:=}\{\vec{\vect{p}}{\in}S\mid \vec{\vect{q}}{\lt}\vec{\vect{p}}\drarrow \vec{\vect{q}}{\not\in}S\}$は有限集合である。
略証.無限集合$S$は$\lt$の無限増加列を含むことを$n$の帰納法で示せばよい。$n{=}1$なら明らか。$S{\subseteq}[\mathbb{N}]^n,\ \pi:[x_i]^n\mapsto[x_i]^{n-1}$とする。$\pi(S)$が有限なら、ある無限集合$\pi^{-1}(\vec{\vect{p}}'){\subseteq}S$は、$n{=}1$と同様に無限増加列を含む。$\pi(S)$が無限なら、帰納法の仮定による$\pi(S)$中の無限増加列$(\pi(\vec{\vect{p}}_i))_{i\in\mathbb{N}}$に対し、$(\vec{\vect{p}}_i)_{i{\in}\mathbb{N}}$は無限増加部分列を含む。
定理.準線形集合は和集合、積集合、線型写像・射影で閉じている。
略証.定義より明らかに和集合と線型写像・射影で閉じている。積集合では、分配法則より線形集合$\vec{\vect{c}}{+}\mathbb{N}{}_p[\vec{\vect{p}}_i],\ \vec{\vect{d}}{+}\mathbb{N}{}_q[\vec{\vect{q}}_j]$の積が準線形であること示せばよい。$L(\vec{\vect{u}},\vec{\vect{v}}){:=}\left\{([x_i]^p,[y_j]^q)\mid \vec{\vect{u}}{+}[x_i]^p{}_p[\vec{\vect{p}}_i]{=}\vec{\vect{v}}{+}[y_j]^q{}_q[\vec{\vect{q}}_j] \right\}$とおけば$L(\vec{\vect{u}},\vec{\vect{v}}){=}\min(L(\vec{\vect{u}},\vec{\vect{v}})){+}\mathbb{N}\min(L(\vec{\vect{0}},\vec{\vect{0}})\setminus \vec{\vect{0}})$。線型写像$\tau:([x_i]^p,[y_j]^q) \mapsto [x_i]^p{}_p[\vec{\vect{p}}_i]$とおいて、$\vec{\vect{c}}{+}\tau(L(\vec{\vect{c}},\vec{\vect{d}})){=}(\vec{\vect{c}}{+}\mathbb{N}{}_p[\vec{\vect{p}}_i]){\cap}(\vec{\vect{d}}{+}\mathbb{N}{}_q[\vect{q}_i])$は準線形集合である。
補題.$A=\{[x_i]^n\mid c{+}[x_i]^n{}_n[p_i]{=}d{+}[x_i]^n{}_n[q_i]\}$は準線型集合である。
略証.$B:=\{[x_i]^n\mid [x_i]^n{}_n[p_i]{=}[x_i]^n{}_n[q_i]\}$とおけば、$A{=}\min(A){+}\mathbb{N}\min(B\setminus \vec{\vect{0}})$。
次に準線形集合が補集合で閉じていることを示す。
定義.${}_m[\vec{\vect{p}}_i]$は(適当に並べ替えて)$\mathbb{N}{}_k[\vec{\vect{p}}_i]\cap\mathbb{N}{}_{m-k}[\vec{\vect{p}}_{i+k}]\ne\emptyset$とできる時従属といい、従属でない時独立という。これは行ベクトルの線型従属・独立と一致する。
補題1.線形集合は独立周期集合(独立周期を持つ線形集合)の和で表される。
証明.周期の本数$m$に関する帰納法で示す。$m{=}1$なら明らか。$L{=}\vec{\vect{c}}{+}\mathbb{N}{}_m[\vec{\vect{p}}_i],$ $[a_i]^k{}_k[\vec{\vect{p}}_i]{=}[a_{i+k}]^{m-k}_{\ \ m-k}[\vec{\vect{p}}_{i+k}]$と仮定し、$Z_j{:=}\{\vec{\vect{c}}{+}b_j\vec{\vect{p}}_j\mid 0{\le}b_j{\lt}a_j\}{+}\mathbb{N}({}_m[\vec{\vect{p}}_i]{\setminus}\vec{\vect{p}}_j)$とおく。明らかに $\bigcup_{j=1}^k Z_j \subseteq L$。逆に $y{:=}\vec{\vect{c}}{+}[b_j]^m{}_m[\vec{\vect{p}}_j] \in L$とする。$\forall j{\le}k( b_j{\ge}a_j)$ならば$y{=}\vec{\vect{c}}{+}[b_j{-}a_j]^k{}_k[\vect{p}_j]{+}[b_{j+k}{+}a_{j+k}]^{m-k}_{\ \ m-k}[\vec{\vect{p}}_{j+k}]$と書ける。これを繰返せばいつかは $\exists j{\le}k( b_j{\lt}a_j)$が成立ち$y{=}\vec{\vect{c}}{+}b_j\vec{\vect{p}}_j{+}\sum_{i=1}^{m\setminus j}b_i\vec{\vect{p}}_i\in Z_j$。($\sum_{i=1}^{m\setminus j}$は$j$を除く$1$から$m$までの和) よって$L{=}\bigcup_{j=1}^k Z_j$。帰納法の仮定より$Z_j,$ $L$は独立周期集合の和になる。
補題2.独立(正則)な${}_n[\vec{\vect{p}}_i]{\in}{}_n[\mathbb{N}]^n$に対し$k_0{\in}\mathbb{N}_+$が存在して、任意の$\vec{\vect{x}}{\in}[\mathbb{N}]^n$に対し
1.$k_\vec{\vect{x}}{:=}\min\{ k{\gt}0 \mid k\vec{\vect{x}}{\in}\mathbb{Z}{}_n[\vec{\vect{p}}_i]\} \lt k_0,$ ($\mathbb{Z}$は整数の集合)
2.$k_\vec{\vect{x}}\vec{\vect{x}}{=}[a_i]^n{}_n[\vec{\vect{p}}_i], k\vec{\vect{x}}{=}[b_i]^n{}_n[\vec{\vect{p}}_i] \in \mathbb{Z}{}_n[\vec{\vect{p}}_i]$ならば、$\exists q{\in}\mathbb{N}((k,[b_i]^n)=q(k_\vec{\vect{x}},[a_i]^n)$
略証.1. $\exists k_0{\gt}0\;k_0({}_n[\vec{\vect{p}}_i])^{-1}{\in}{}_n[\mathbb{Z}]^n$より、$ k_0\vec{\vect{x}}=(\vec{\vect{x}}(k_0({}_n[\vec{\vect{p}}_i])^{-1})){}_n[\vec{\vect{p}}_i] \in\mathbb{Z}{}_n[\vec{\vect{p}}_i]$。
2. $r_\vec{\vect{x}}{=}k{-}qk_\vec{\vect{x}}{\lt}k_\vec{\vect{x}} \drarrow r_\vec{\vect{x}}\vec{\vect{x}}{=}\sum_{i=1}^n(b_i{-}qa_i)\vec{\vect{p}}_i$より $r_\vec{\vect{x}}{=}0 \wedge \bigwedge_{i=1}^n b_i{=}qa_i$。
補題3.独立な${}_m[\vec{\vect{p}}_i]\in {}_m[\mathbb{N}]^n$に対し$(\mathbb{N}{}_m[\vec{\vect{p}}_i])^\complement$は準線形集合である。
略証.必要なら単位ベクトル$\vec{\vect{e}}_k$を追加して独立な${}_n[\vec{\vect{p}}_i]{=}{}_n[p_{ij}]^n \in {}_n[\mathbb{N}]^n$を構成し、$k_0$を補題2の正整数とする。補題2より$\vec{\vect{y}}{=}[y_i]^n,$として $\displaystyle \vec{\vect{x}}{\in}\mathbb{N}{}_m[\vec{\vect{p}}_i] \rightleftarrows \forall \vec{\vect{y}}{\in}[\mathbb{Z}]^n \bigwedge_{k=1}^{k_0}\left(k\vec{\vect{x}}{=}\vec{\vect{y}}{}_n[\vec{\vect{p}}_i] \drarrow \bigwedge_{i=1}^m y_i{\ge}0 \wedge\bigwedge_{i\gt m}^n y_i{=}0 \wedge\bigwedge_{i=1}^n k\pmb{|}y_i \right)$
$\displaystyle \vec{\vect{x}}{\not\in}\mathbb{N}{}_m[\vec{\vect{p}}_i] \rightleftarrows \exists \vec{\vect{y}}{\in}[\mathbb{Z}]^n \bigvee_{k=1}^{k_0} \left(k\vec{\vect{x}}{=}\vec{\vect{y}}{}_n[\vec{\vect{p}}_i] \wedge \left(\bigvee_{i=1}^m y_i{\lt}0 \vee\bigvee_{i\gt m}^n y_i{\ne}0 \vee\bigvee_{i=1}^n k{\not\pmb{|}} y_i \right)\right)$
$\displaystyle \rightleftarrows \exists \vec{\vect{y}}{\in}[\mathbb{N}]\ \bigvee_{k=1}^{k_0}\bigvee_{I\subseteq \{1..n\}} \displaystyle \left(\bigwedge_{j=1}^n kx_j{+}\sum_{i\in I} y_ip_{ij}{=}\sum_{i\not\in I} y_ip_{ij} \wedge \left(\bigvee_{i\in I}\bigvee_{i\gt m}^n y_i{\gt}0 \vee\bigvee_{i=1}^n k{\not\pmb{|}}y_i \right)\right)$
問・補題と、準線形集合は和、積、射影で閉じているから、定理が成立つ。
定義.${}_m[\vec{\vect{p}}_i]$は(適当に並べ替えて)$\mathbb{N}{}_k[\vec{\vect{p}}_i]\cap\mathbb{N}{}_{m-k}[\vec{\vect{p}}_{i+k}]\ne\emptyset$とできる時従属といい、従属でない時独立という。これは行ベクトルの線型従属・独立と一致する。
補題1.線形集合は独立周期集合(独立周期を持つ線形集合)の和で表される。
証明.周期の本数$m$に関する帰納法で示す。$m{=}1$なら明らか。$L{=}\vec{\vect{c}}{+}\mathbb{N}{}_m[\vec{\vect{p}}_i],$ $[a_i]^k{}_k[\vec{\vect{p}}_i]{=}[a_{i+k}]^{m-k}_{\ \ m-k}[\vec{\vect{p}}_{i+k}]$と仮定し、$Z_j{:=}\{\vec{\vect{c}}{+}b_j\vec{\vect{p}}_j\mid 0{\le}b_j{\lt}a_j\}{+}\mathbb{N}({}_m[\vec{\vect{p}}_i]{\setminus}\vec{\vect{p}}_j)$とおく。明らかに $\bigcup_{j=1}^k Z_j \subseteq L$。逆に $y{:=}\vec{\vect{c}}{+}[b_j]^m{}_m[\vec{\vect{p}}_j] \in L$とする。$\forall j{\le}k( b_j{\ge}a_j)$ならば$y{=}\vec{\vect{c}}{+}[b_j{-}a_j]^k{}_k[\vect{p}_j]{+}[b_{j+k}{+}a_{j+k}]^{m-k}_{\ \ m-k}[\vec{\vect{p}}_{j+k}]$と書ける。これを繰返せばいつかは $\exists j{\le}k( b_j{\lt}a_j)$が成立ち$y{=}\vec{\vect{c}}{+}b_j\vec{\vect{p}}_j{+}\sum_{i=1}^{m\setminus j}b_i\vec{\vect{p}}_i\in Z_j$。($\sum_{i=1}^{m\setminus j}$は$j$を除く$1$から$m$までの和) よって$L{=}\bigcup_{j=1}^k Z_j$。帰納法の仮定より$Z_j,$ $L$は独立周期集合の和になる。
補題2.独立(正則)な${}_n[\vec{\vect{p}}_i]{\in}{}_n[\mathbb{N}]^n$に対し$k_0{\in}\mathbb{N}_+$が存在して、任意の$\vec{\vect{x}}{\in}[\mathbb{N}]^n$に対し
1.$k_\vec{\vect{x}}{:=}\min\{ k{\gt}0 \mid k\vec{\vect{x}}{\in}\mathbb{Z}{}_n[\vec{\vect{p}}_i]\} \lt k_0,$ ($\mathbb{Z}$は整数の集合)
2.$k_\vec{\vect{x}}\vec{\vect{x}}{=}[a_i]^n{}_n[\vec{\vect{p}}_i], k\vec{\vect{x}}{=}[b_i]^n{}_n[\vec{\vect{p}}_i] \in \mathbb{Z}{}_n[\vec{\vect{p}}_i]$ならば、$\exists q{\in}\mathbb{N}((k,[b_i]^n)=q(k_\vec{\vect{x}},[a_i]^n)$
略証.1. $\exists k_0{\gt}0\;k_0({}_n[\vec{\vect{p}}_i])^{-1}{\in}{}_n[\mathbb{Z}]^n$より、$ k_0\vec{\vect{x}}=(\vec{\vect{x}}(k_0({}_n[\vec{\vect{p}}_i])^{-1})){}_n[\vec{\vect{p}}_i] \in\mathbb{Z}{}_n[\vec{\vect{p}}_i]$。
2. $r_\vec{\vect{x}}{=}k{-}qk_\vec{\vect{x}}{\lt}k_\vec{\vect{x}} \drarrow r_\vec{\vect{x}}\vec{\vect{x}}{=}\sum_{i=1}^n(b_i{-}qa_i)\vec{\vect{p}}_i$より $r_\vec{\vect{x}}{=}0 \wedge \bigwedge_{i=1}^n b_i{=}qa_i$。
補題3.独立な${}_m[\vec{\vect{p}}_i]\in {}_m[\mathbb{N}]^n$に対し$(\mathbb{N}{}_m[\vec{\vect{p}}_i])^\complement$は準線形集合である。
略証.必要なら単位ベクトル$\vec{\vect{e}}_k$を追加して独立な${}_n[\vec{\vect{p}}_i]{=}{}_n[p_{ij}]^n \in {}_n[\mathbb{N}]^n$を構成し、$k_0$を補題2の正整数とする。補題2より$\vec{\vect{y}}{=}[y_i]^n,$として $\displaystyle \vec{\vect{x}}{\in}\mathbb{N}{}_m[\vec{\vect{p}}_i] \rightleftarrows \forall \vec{\vect{y}}{\in}[\mathbb{Z}]^n \bigwedge_{k=1}^{k_0}\left(k\vec{\vect{x}}{=}\vec{\vect{y}}{}_n[\vec{\vect{p}}_i] \drarrow \bigwedge_{i=1}^m y_i{\ge}0 \wedge\bigwedge_{i\gt m}^n y_i{=}0 \wedge\bigwedge_{i=1}^n k\pmb{|}y_i \right)$
$\displaystyle \vec{\vect{x}}{\not\in}\mathbb{N}{}_m[\vec{\vect{p}}_i] \rightleftarrows \exists \vec{\vect{y}}{\in}[\mathbb{Z}]^n \bigvee_{k=1}^{k_0} \left(k\vec{\vect{x}}{=}\vec{\vect{y}}{}_n[\vec{\vect{p}}_i] \wedge \left(\bigvee_{i=1}^m y_i{\lt}0 \vee\bigvee_{i\gt m}^n y_i{\ne}0 \vee\bigvee_{i=1}^n k{\not\pmb{|}} y_i \right)\right)$
$\displaystyle \rightleftarrows \exists \vec{\vect{y}}{\in}[\mathbb{N}]\ \bigvee_{k=1}^{k_0}\bigvee_{I\subseteq \{1..n\}} \displaystyle \left(\bigwedge_{j=1}^n kx_j{+}\sum_{i\in I} y_ip_{ij}{=}\sum_{i\not\in I} y_ip_{ij} \wedge \left(\bigvee_{i\in I}\bigvee_{i\gt m}^n y_i{\gt}0 \vee\bigvee_{i=1}^n k{\not\pmb{|}}y_i \right)\right)$
問・補題と、準線形集合は和、積、射影で閉じているから、定理が成立つ。
定理.準線形集合の補集合は準線形集合である。
証明.補題1より準線形集合は独立周期集合の和で、独立周期集合の補集合$(\vec{\vect{c}}{+}\mathbb{N}{}_m[\vec{\vect{p}}_i])^\complement \displaystyle{=}(\vec{\vect{c}}{+}(\mathbb{N}{}_m[\vec{\vect{p}}_i])^\complement) {\cup}\{\vec{\vect{x}}\mid \bigvee_{i=1}^n\bigvee_{k=0}^{c_i-1} x_i{=}k\}$は補題3より準線形集合である。
プレスバーガー論理
「集合と論理の記法」では、論理記号(語)としての、$\wedge,\vee,\neg,\drarrow,\forall,\exists$の働きを解説し、本節の議論ではそれらの記号を多用した。ここでは、自然数(非負整数)とその加算に対する1階述語論理であるプレスバーガー論理$\mathfrak{P}$の記述能力が準線形集合と一致することを示そう。まず。$\mathfrak{P}$を再帰的に定義する。
$\mathfrak{P}$の項は、加算が可換だから$a{+}\sum_{i=1}^nb_ix_i$の形に書け、補題より$(t_1{=}t_2)^\top$は準線形集合である。準線形集合は和、補集合、射影で閉じているから、$\mathfrak{P}$集合は準線形集合である。略記$t_1{\le}t_2:\equiv \exists x(t_1{+}x{=}t_2),$ $\varphi{\wedge}\psi:\equiv\neg(\neg\varphi{\vee}\neg\psi),$ $\forall x\psi:\equiv\neg\exists\,\neg\psi$を用いれば、逆に(準)線形集合が$\mathfrak{P}$論理式で記述できることは明らかだろう。
注.$t_1{=}t_2\rightleftarrows t_1{\le}t_2 \wedge t_2{\le}t_1$であるから、$=$と$\le$はどちらを$\mathfrak{P}$の定義に含めどちらを略記にしてもよい。同様に$\neg$の他に$\wedge, \vee$のどちらを定義に選んでも、他方を略記とできる。
$\cdots$集合のクラスを$\mathfrak{C}(\cdots$集合$)$と表す。
定理.$\mathfrak{C}($準線形集合$)=\mathfrak{C}(\mathfrak{P}$集合$)$。
証明.補題1より準線形集合は独立周期集合の和で、独立周期集合の補集合$(\vec{\vect{c}}{+}\mathbb{N}{}_m[\vec{\vect{p}}_i])^\complement \displaystyle{=}(\vec{\vect{c}}{+}(\mathbb{N}{}_m[\vec{\vect{p}}_i])^\complement) {\cup}\{\vec{\vect{x}}\mid \bigvee_{i=1}^n\bigvee_{k=0}^{c_i-1} x_i{=}k\}$は補題3より準線形集合である。
プレスバーガー論理
「集合と論理の記法」では、論理記号(語)としての、$\wedge,\vee,\neg,\drarrow,\forall,\exists$の働きを解説し、本節の議論ではそれらの記号を多用した。ここでは、自然数(非負整数)とその加算に対する1階述語論理であるプレスバーガー論理$\mathfrak{P}$の記述能力が準線形集合と一致することを示そう。まず。$\mathfrak{P}$を再帰的に定義する。
- $\mathfrak{P}$は論理記号の他に、定数$a{\in}\mathbb{N}$と変数$x,y,\dots$、加算記号$+$、等号$=$を持つ
- 定数や変数は$\mathfrak{P}$の項であり、$t_1,t_2$が$\mathfrak{P}$の項ならば、$t_1{+}t_2$は$\mathfrak{P}$の項であり、$t_1{=}t_2$は$\mathfrak{P}$の論理式である
-
$\varphi,\psi$が$\mathfrak{P}$の論理式ならば、$\varphi\vee \psi, \neg\psi, \exists x\,\psi$も$\mathfrak{P}$の論理式である。
$\mathfrak{P}$の項は、加算が可換だから$a{+}\sum_{i=1}^nb_ix_i$の形に書け、補題より$(t_1{=}t_2)^\top$は準線形集合である。準線形集合は和、補集合、射影で閉じているから、$\mathfrak{P}$集合は準線形集合である。略記$t_1{\le}t_2:\equiv \exists x(t_1{+}x{=}t_2),$ $\varphi{\wedge}\psi:\equiv\neg(\neg\varphi{\vee}\neg\psi),$ $\forall x\psi:\equiv\neg\exists\,\neg\psi$を用いれば、逆に(準)線形集合が$\mathfrak{P}$論理式で記述できることは明らかだろう。
注.$t_1{=}t_2\rightleftarrows t_1{\le}t_2 \wedge t_2{\le}t_1$であるから、$=$と$\le$はどちらを$\mathfrak{P}$の定義に含めどちらを略記にしてもよい。同様に$\neg$の他に$\wedge, \vee$のどちらを定義に選んでも、他方を略記とできる。
$\cdots$集合のクラスを$\mathfrak{C}(\cdots$集合$)$と表す。
定理.$\mathfrak{C}($準線形集合$)=\mathfrak{C}(\mathfrak{P}$集合$)$。
補遺1.集合の濃度とパラドックス
無限を数える:集合の濃度集合$A$のサイズ$|A|$を無限集合に定義しようとすると、困難に直面する。有限集合では当り前な2つの原則(直感) ① $A\subset B\drarrow |A|\lt|B|$、と ② $A$と$B$の要素が1対1対応すれば$|A|=|B|$、とが相反する。例えば、自然数の集合$\mathbb{N}$に対し、$2\mathbb{N}:=\{2n\mid n\in\mathbb{N}\}$(偶数の集合)とおけば
① $2\mathbb{N}\subset\mathbb{N}$なので$|2\mathbb{N}|\lt|\mathbb{N}|$
② $f:n\mapsto 2n$は1対1対応なので$|\mathbb{N}|=|2\mathbb{N}|$
問.1. ②の意味で$|\mathbb{N}_+|=|\mathbb{N}|$を示せ。
2. 無限の$1,2,\dots$号室を持つ「ホテル無限」がある。満室のある日、次の状況でも支配人はお客を泊めたという。
(1) 新たにお客が一人やってきた。どうしたか。
(2) 新たに無限人数の団体客がやってきた。どうしたか。
集合の濃度
カントールは、①'$A\subseteq B \drarrow |A|\le |B|$と②を採用して、$|A|$を$A$の濃度と呼んだ。正確な定義を与えるために、次の定理を準備しよう。
$f:A\to B$は $x{=}y\darrow{\rightarrow}{\leftarrow}f(x){=}f(y)$ を満たす時単射といい、単射かつ$f(A):=\{f(a)\mid a\in A\}=B$(全射)の時、1対1対応(全単射)という。
定理.単射$f:A\to B,\ g:B\to A$があれば、1対1対応$h:A\to B$がある。
証明.$C_0:=A\setminus g(B),\ C_{n+1}:=g(f(C_n)),\ C:=\bigcup_{n=0}^\infty C_n\subseteq A$ とおくと、$A\setminus C\subseteq A\setminus C_0\subseteq g(B)$。$g$は単射だから、$g^{-1}:g(b)\mapsto b$は$g(B){\to}B$の1対1対応で、$h(x):=\begin{cases}f(x)& \dlarrow x{\in}C\\g^{-1}(x)& \dlarrow x{\in} A{\setminus}C\end{cases}$ も1対1対応である。実際、$x{\in}C_i,\ y{\in}A{\setminus}C$に対し $g^{-1}(y){=}f(x)$なら$y{=}g(f(x))\in C_{i+1}{\subseteq}C$となり矛盾だから$h$は単射。一方$C_0{\cap}g(B){=}\emptyset$より、$g^{-1}(C_0){=}\emptyset,$ $g^{-1}(C){=}\bigcup_{i=1}^\infty g^{-1}(g(f(C_{i-1}))){=}\bigcup_{i=0}^\infty f(C_i){=}f(C)$。よって $h(A){=}g^{-1}(A\setminus C){\cup}f(C){=}(g^{-1}(A){\setminus}g^{-1}(C)){\cup}f(C){\supseteq}g^{-1}(A){=}B$。
定義.$|A|{\le}|B|$を単射$f:A\to B$が存在する事と定義し、$|A|{=}|B|:= |A|{\le}|B|\wedge |B|{\le}|A|$、$|A|{\lt}|B|:= |A|{\le}|B|\wedge |A|{\ne}|B|$と定義する。
定理.$|A|\lt |\mathbb{2}^A|$。よって、いくらでも大きな濃度が存在する。
証明.$|A|\le |\mathbb{2}^A|$は明らか。$f:A\to \mathbb{2}^A$とし$B:=\{x\mid x\not\in f(x)\}=f(b)$とおくと、$b\in B\Leftrightarrow b\not\in f(b){=}B$より矛盾。即ち全射$f(A)=\mathbb{2}^A$はない。
$\mathbb{Z},\mathbb{Q},\mathbb{R}$で各々整数,有理数,実数の集合を表す。$A^*$で$A$の要素の有限列$a_{1..n},\ n{\ge}0$の集合を、$A^\mathbb{N}$で$A$の要素の無限列$a_{1..}$の集合を表す。
定理.$|\mathbb{N}|{=}|\mathbb{Z}|{=}|\mathbb{Q}|{=}|\mathbb{N}^*| \lt |\mathbb{2}^\mathbb{N}|{=}|\mathbb{R}|{=}|\mathbb{R}^\mathbb{N}|$。$|\Sigma|\in\mathbb{N}\setminus\mathbb{2} \drarrow |\Sigma^*|{=}|\mathbb{N}| \wedge |\Sigma^\mathbb{N}|{=}|\mathbb{R}|$。
略証.$\mathbb{N}_+^*$の要素(数列)は、和の小さい順に(分けて)過不足なく並べられる。
$(),(1),(2),(1,1),(3),(1,2),(2,1),(1,1,1),(4),(1,3),(2,2),(3,1),(1,1,2),\cdots$
よって、$|\mathbb{N}|{=}|\mathbb{N}_+^*|{=}|\mathbb{N}^*|$。$r\in\mathbb{2}^\mathbb{N}$を1未満のある10進正実数の小数点以下と一意に見做せるから$|\mathbb{2}^\mathbb{N}|{\le}|\mathbb{R}|$。実数は無限長小数で表わせ、$\Sigma$の要素は$0,1$列で符号化できるから$|\mathbb{R}|{\le}|\{-,.,0,1,\cdots,9\}^\mathbb{N}|{\le}|\mathbb{2}^\mathbb{N}|$。$|\mathbb{R}^\mathbb{N}|{=}|(\mathbb{2}^\mathbb{N})^\mathbb{N}|{=}|\mathbb{2}^{\mathbb{N}\times\mathbb{N}}|{=}|\mathbb{2}^\mathbb{N}|$。
問.稠密性と濃度比較
(1) (有限長の)表現を持つ実数はどのくらいあるか。
(2) 無理数から実数への全単射を(1つ)与えよ。
(3) 数直線上で有理数はどのように分布しているか。
ラッセルのパラドックス
集合を規定する1変数述語は何でも許される訳ではない。実際、$M=\{x|x\not\in x\}$「『自分自身を要素として含まない集合』の集合」を認めると、$M\in M \Leftrightarrow M \not\in M$ となって矛盾する。
では集合とは何か?について直観的に理解しやすい定義は知られていないように思われるが、ここでは深入りしない。
定理.$|A|\lt |\mathbb{2}^A|$。よって、いくらでも大きな濃度が存在する。
証明.$|A|\le |\mathbb{2}^A|$は明らか。$f:A\to \mathbb{2}^A$とし$B:=\{x\mid x\not\in f(x)\}=f(b)$とおくと、$b\in B\Leftrightarrow b\not\in f(b){=}B$より矛盾。即ち全射$f(A)=\mathbb{2}^A$はない。
$\mathbb{Z},\mathbb{Q},\mathbb{R}$で各々整数,有理数,実数の集合を表す。$A^*$で$A$の要素の有限列$a_{1..n},\ n{\ge}0$の集合を、$A^\mathbb{N}$で$A$の要素の無限列$a_{1..}$の集合を表す。
定理.$|\mathbb{N}|{=}|\mathbb{Z}|{=}|\mathbb{Q}|{=}|\mathbb{N}^*| \lt |\mathbb{2}^\mathbb{N}|{=}|\mathbb{R}|{=}|\mathbb{R}^\mathbb{N}|$。$|\Sigma|\in\mathbb{N}\setminus\mathbb{2} \drarrow |\Sigma^*|{=}|\mathbb{N}| \wedge |\Sigma^\mathbb{N}|{=}|\mathbb{R}|$。
略証.$\mathbb{N}_+^*$の要素(数列)は、和の小さい順に(分けて)過不足なく並べられる。
問.稠密性と濃度比較
(1) (有限長の)表現を持つ実数はどのくらいあるか。
(2) 無理数から実数への全単射を(1つ)与えよ。
(3) 数直線上で有理数はどのように分布しているか。
ラッセルのパラドックス
集合を規定する1変数述語は何でも許される訳ではない。実際、$M=\{x|x\not\in x\}$「『自分自身を要素として含まない集合』の集合」を認めると、$M\in M \Leftrightarrow M \not\in M$ となって矛盾する。
では集合とは何か?について直観的に理解しやすい定義は知られていないように思われるが、ここでは深入りしない。
補遺2.アリストテレスの名辞論理:中世までの論理学
中世までの論理学の主流であるアリストテレスの名辞論理を簡単に紹介する。中世論理学では「3段論法をどう覚え適用できるか」が重要であり、覚え歌があった。実は、名辞は非空集合であり、名辞論理を集合の記法で解釈できる。名辞論理の基本形には以下の4型がある($A,B\ne\emptyset$は名辞)
| A型 | すべての$A$は$B$である | $A\subseteq B$ | I型 | ある$A$は$B$である | $A\cap B\ne\emptyset$ |
| E型 | すべての$A$は$B$でない | $A\cap B=\emptyset$ | O型 | ある$A$は$B$でない | $A-B\ne\emptyset$ |
三段論法には大/小前提から結論を導く際の「AはB」の配置で4格ある。
| 第1格 | 第2格 | 第3格 | 第4格 | 例.EAO型第1格 | 集合解釈 | |
| 大前提 | $B$は$C$ | $C$は$B$ | $B$は$C$ | $C$は$B$ | (E)すべての$B$は$C$でない | $B\cap C=\emptyset$ |
| 小前提 | $A$は$B$ | $A$は$B$ | $B$は$A$ | $B$は$A$ | (A)すべての$A$は$B$である | $A\subseteq B$ |
| 結論 | $A$は$C$ | $A$は$C$ | $A$は$C$ | $A$は$C$ | 故に(O)ある$A$は$C$でない | $\therefore A-C\ne\emptyset$ |
三段論法の覚え歌(ウィキペディア)
アリストテレスは、AAA型第1格~OOO型第4格まで$4^4=256$通り中の妥当な三段論法$24$通りを、第1格の妥当なAAA,EAE,AII,EIO型からの同値変形で証明した。それらは覚え歌中の19個(青/赤字)に加えて、結論A,E(赤字)に対する自明な推論A$\drarrow$I、E$\drarrow$O(名辞の非空集合性による)から得られる。(下表)
Barbara celarent darii ferioque prioris.第1格
Cesare camestres festino baroco secundoe.第2格
Tertia darapti disamis datisi felapton, bocardo ferison habet.第3格
Quarta insuper addit bramantip camenes dimaris fesapo fresison.第4格
| 第1格 | AAA, AAI, EAE, EAO, AII, EIO | 第2格 | EAE, EAO, AEE, AEO, EIO, AOO |
| 第3格 | AAI, IAI, AII, EAO, OAO, EIO | 第4格 | AAI, AEE, AEO, IAI, EAO, EIO |
問.EAO型第1格三段論法が妥当であることを集合記法で確かめよ。