この章の目標
この章では、文脈自由文法(CFG)とプッシュダウンオートマトンの等価性を示し、それらが定める言語、文脈自由言語を扱う。定義.同値な次の3条件をみたす言語$L$を文脈自由言語(CFL)という。
①$L$はCFGで生成される
②$L$は$\varepsilon$受理PDAで認識される
③$L$は状態受理PDAで認識される
その上で、本章では、次の事柄を学ぶ。
・文脈自由言語の諸性質を学びます
・言語が文脈自由言語であるための必要十分条件を学びます
・非文脈自由言語の例を示します
オートマトンの動作やや文法の導出のデモにJFLAPを利用します
文脈自由文法(CFG)
文法$G=(\Gamma,\Sigma,P,S)$で、規則が$A\to\alpha(A\in \Gamma,\ \alpha\in (\Sigma\,\dot\cup\,\Gamma)^*)$の形をしているものを文脈自由文法(CFG)という。$\mathcal{L}(A,G):=\{\vect{w}\in \Sigma^*\mid A\overset{*}\drarrow \vect{w}\}$を$G$で$A$が生成する言語といい、$\mathcal{L}(G):=\mathcal{L}(S,G)$を$G$が生成する言語という。以下誤解が生じなければ、CFGはその規則のみを与え、開始記号の規則を最初に書くものとする。
例.CFG $G:S\to 0S1 \mid \varepsilon$ は$\{0^n1^n\mid n\in\mathbb{N}\}$を生成する
$\because)\ S\Rightarrow 0S1\Rightarrow 00S11\overset{*}\Rightarrow 0^nS1^n\Rightarrow 0^n1^n$
パズル.$\{\vect{w}\vect{w}^R|\vect{w}\in\{0,1\}^*\}$を生成するCFGを示せ
例.括弧$[,]$の対応の取れた列の言語(集合)$L$を生成するCFGを考えよう。$\vect{w}\in L\setminus\varepsilon$は、頭の$[$に対応する$]$を必ず持つから、$\vect{w}=[\vect{u}]\vect{v}$と書けて$\vect{u},\vect{v}\in L$である。したがって、$L$は次のように帰納的に定義できる。
また、正則文法と言語の方程式と同様の議論により、$L$は言語の方程式$S=[S]S\cup \{\varepsilon\}$の最小解である。一般に、CFG$G=(\Gamma,\Sigma,P.S)$(の規則)は、言語$\mathcal{L}(A,G), A{\in}\Gamma$の同時再帰的定義や(最小解を定める)連立方程式と同一視できる。
導出木
 文脈自由文法$G=(\Gamma,\Sigma,P,S)$の導出過程を表す導出木は次のように帰納的に定義される。
文脈自由文法$G=(\Gamma,\Sigma,P,S)$の導出過程を表す導出木は次のように帰納的に定義される。
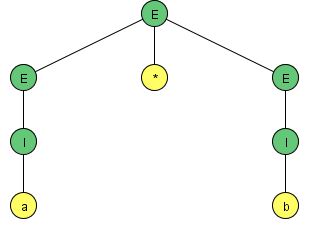
例.単純な式を生成する文法 $G_1:\begin{cases}E\to I\mid E+E\mid E*E\mid (E)\\ I\to a\mid b\mid Ia\mid Ib\mid I0\mid I1\end{cases}$ において
$a*b$の導出木は1つ(右上図)であるが、本質的に同じ導出を複数持つ。
$\left\{\begin{eqnarray}E&\Rightarrow&E*E&\Rightarrow&I*E&\Rightarrow&a*E&\Rightarrow&a*I&\Rightarrow&a*b (\color{blue}{最左導出})\\E&\Rightarrow&E*E&\Rightarrow&E*I&\Rightarrow&E*b&\Rightarrow&I*b&\Rightarrow&a*b (\color{blue}{最右導出})\end{eqnarray}\right.$
ここで、最左(右)導出とは、常に最も左(右)の非終端記号に規則を適用する導出を言い、各々構文木と1対1に対応する。
パズル.文法$G_1$で$a+b*a$は複数の(完了)導出木を持つことを示せ。ヒント
文脈自由文法は、同じ文字列に対し複数の(完了)導出木を持つ場合があるとき、あいまいであるという。前ページの例では、同じ言語を生成するあいまいでない文脈自由文法 $G_2:\begin{cases} E \to E+T\mid T\\ T \to I\mid T*T\mid I\mid (E)\\ I \to a\mid b\mid Ia\mid Ib\mid I0\mid I1\end{cases}$ が存在する。
パズル.上の文法で$a+b*a$の導出木を示せ。
- 頂点$S$だけからなる木は導出木である。
- 規則$A\to X_1X_2\cdots X_n\in P$に対し、導出木の葉(子の無い頂点)$A$に$n$個の子頂点$X_1,X_2,\dots,X_n$を左から順に付けた木は導出木である。
例.単純な式を生成する文法 $G_1:\begin{cases}E\to I\mid E+E\mid E*E\mid (E)\\ I\to a\mid b\mid Ia\mid Ib\mid I0\mid I1\end{cases}$ において
$a*b$の導出木は1つ(右上図)であるが、本質的に同じ導出を複数持つ。
$\left\{\begin{eqnarray}E&\Rightarrow&E*E&\Rightarrow&I*E&\Rightarrow&a*E&\Rightarrow&a*I&\Rightarrow&a*b (\color{blue}{最左導出})\\E&\Rightarrow&E*E&\Rightarrow&E*I&\Rightarrow&E*b&\Rightarrow&I*b&\Rightarrow&a*b (\color{blue}{最右導出})\end{eqnarray}\right.$
ここで、最左(右)導出とは、常に最も左(右)の非終端記号に規則を適用する導出を言い、各々構文木と1対1に対応する。
パズル.文法$G_1$で$a+b*a$は複数の(完了)導出木を持つことを示せ。ヒント
文脈自由文法は、同じ文字列に対し複数の(完了)導出木を持つ場合があるとき、あいまいであるという。前ページの例では、同じ言語を生成するあいまいでない文脈自由文法 $G_2:\begin{cases} E \to E+T\mid T\\ T \to I\mid T*T\mid I\mid (E)\\ I \to a\mid b\mid Ia\mid Ib\mid I0\mid I1\end{cases}$ が存在する。
パズル.上の文法で$a+b*a$の導出木を示せ。
この例はまた、文脈自由文法に対する新たな洞察を与える。数式の意味(乗算を先に行う)を考えれば、ヒントの導出木で(a)は正しく(b)は正しくない。即ち、文脈自由文法の導出木は、生成列を“解釈”する(例では数式を計算する)手がかりを与える。この意味で、上の文法$G_2$は“意味的に正しい”導出木を与える文法である。このような文脈では、導出木を構文木ともいう。
パズル.「頭が赤い魚を食べる猫の赤ちゃん」は何通りに解釈できるか。
CFLは、それを生成するCFGがすべてあいまいであるとき、(本質的に)あいまいであるという。CFL $L=\{a^mb^mc^nd^n,\ a^mb^nc^nd^m\mid n,m\ge 0\}$が(本質的に)あいまいであることを厳密ではないが直感的に説明しよう。CFG $G=(\Gamma,\Sigma,P,S)$に対し$\mathcal{L}(G)=L$とする。後述の反復原理でも示すが、$L$の十分長い文字列の導出には
$S{\overset{*}\Rightarrow}\vect{u}A\vect{y}{\overset{*}\Rightarrow}\vect{u}\vect{v}A\vect{x}\vect{y}{\overset{*}\Rightarrow}\vect{u}\vect{v}\vect{w}\vect{x}\vect{y} \wedge \vect{v}\vect{x}{\ne}\varepsilon$と書け、$\forall k\in\mathbb{N}\ \vect{u}\vect{v}^k\vect{w}\vect{x}^k\vect{y}\in L$
となる$A\in\Gamma$が存在する。このような非終端記号$A$を$\vect{v}$と$\vect{x}$の形で分けると、
① $\vect{v}{\in}a^+\wedge\vect{x}{\in}b^+\wedge |\vect{v}|{=}|\vect{x}|$、② $\vect{v}{\in} c^+\wedge\vect{x}{\in}d^+\wedge |\vect{v}|{=}|\vect{x}|$、
③ $\vect{v}{\in}a^+\wedge\vect{x}{\in}d^+\wedge |\vect{v}|{=}|\vect{x}|$、④ $\vect{v}{\in}b^+\wedge\vect{x}{\in}c^+\wedge |\vect{v}|{=}|\vect{x}|$、
という、$L$の定義の$m,\ n$に対応した4種に分類され、同じ導出の中では①②タイプの非終端記号と③④タイプの非終端記号は混在しない(さもなければ$L$に属さない語が生成されてしまう)。したがって、$a^pb^pc^{2p}d^{2p}$の形の十分長い語が①②を使って生成され、$a^qb^{2q}c^{2q}d^q$の形の十分長い語が③④を使って生成されるから、$a^{2p+2q}b^{2p+2q}c^{2p+2q}d^{2p+2q}$ の構文木には①②の非終端記号を使ったものと③④の非終端記号を使ったものの2種類が存在する。
パズル.$L$を生成するCFGを求めよ。
パズル.「頭が赤い魚を食べる猫の赤ちゃん」は何通りに解釈できるか。
CFLは、それを生成するCFGがすべてあいまいであるとき、(本質的に)あいまいであるという。CFL $L=\{a^mb^mc^nd^n,\ a^mb^nc^nd^m\mid n,m\ge 0\}$が(本質的に)あいまいであることを厳密ではないが直感的に説明しよう。CFG $G=(\Gamma,\Sigma,P,S)$に対し$\mathcal{L}(G)=L$とする。後述の反復原理でも示すが、$L$の十分長い文字列の導出には
$S{\overset{*}\Rightarrow}\vect{u}A\vect{y}{\overset{*}\Rightarrow}\vect{u}\vect{v}A\vect{x}\vect{y}{\overset{*}\Rightarrow}\vect{u}\vect{v}\vect{w}\vect{x}\vect{y} \wedge \vect{v}\vect{x}{\ne}\varepsilon$と書け、$\forall k\in\mathbb{N}\ \vect{u}\vect{v}^k\vect{w}\vect{x}^k\vect{y}\in L$
となる$A\in\Gamma$が存在する。このような非終端記号$A$を$\vect{v}$と$\vect{x}$の形で分けると、
① $\vect{v}{\in}a^+\wedge\vect{x}{\in}b^+\wedge |\vect{v}|{=}|\vect{x}|$、② $\vect{v}{\in} c^+\wedge\vect{x}{\in}d^+\wedge |\vect{v}|{=}|\vect{x}|$、
③ $\vect{v}{\in}a^+\wedge\vect{x}{\in}d^+\wedge |\vect{v}|{=}|\vect{x}|$、④ $\vect{v}{\in}b^+\wedge\vect{x}{\in}c^+\wedge |\vect{v}|{=}|\vect{x}|$、
という、$L$の定義の$m,\ n$に対応した4種に分類され、同じ導出の中では①②タイプの非終端記号と③④タイプの非終端記号は混在しない(さもなければ$L$に属さない語が生成されてしまう)。したがって、$a^pb^pc^{2p}d^{2p}$の形の十分長い語が①②を使って生成され、$a^qb^{2q}c^{2q}d^q$の形の十分長い語が③④を使って生成されるから、$a^{2p+2q}b^{2p+2q}c^{2p+2q}d^{2p+2q}$ の構文木には①②の非終端記号を使ったものと③④の非終端記号を使ったものの2種類が存在する。
パズル.$L$を生成するCFGを求めよ。
プッシュダウンオートマトン(PDA)
プッシュダウンオートマトン(PDA PushDown Automaton)$M=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)$ は以下から構成される。- 状態の有限集合 $Q$
- 入力記号の有限集合 $\Sigma$
- スタック記号の有限集合 $\Gamma$
- 遷移の有限集合 $\delta\subseteq Q\times\Sigma^?\times\Gamma\times\Gamma^*\times Q$
- 開始状態 $q_0\in Q$
- スタックの開始記号 $Z\in \Gamma$
- 受理状態の集合 $F \subseteq Q$
PDA$M$は入力(文字列)$\vect{w}$に対し、ある動作列があって
- $Z]q_0\vect{w}\VDASH{}{*}\alpha]q,\ q{\in}F$となるとき、$\vect{w}$を状態受理するといい、$M$が状態受理する文字列の集合を$\mathcal{L}(M)$と表す。
- $Z]q_0\vect{w}\VDASH{}{*}{]}q$ となるとき、$\vect{w}$を$\varepsilon$受理するといい。$M$が$\varepsilon$受理する文字列の集合を$\mathcal{L}_\varepsilon(M)$と表す。
注.スタックに積む動作をプッシュダウン、取出す動作ポップアップという。
例.$\vect{w}\vect{w}^R$を受理するPDA
は語$\vect{w}\vect{w}^R$を受理する。
| $Z]q_01111$ | $\;\vdash\;$ | $Z]q_11111$ | $\;\vdash\;$ | $Z]q_21111$ |
| $\vdash$ | ||||
| $1Z]q_0111$ | $\vdash$ | $1Z]q_1111$ | $\vdash$ | $Z]q_111$ |
| $\vdash$ | $\vdash$ | |||
| $11Z]q_011$ | $\vdash$ | $11Z]q_111$ | $Z]q_211$ | |
| $\vdash$ | $\vdash$ | |||
| $111Z]q_01$ | $\vdash$ | $111Z]q_11$ | $1Z]q_11$ | |
| $\vdash$ | $\vdash$ | $\vdash$ | ||
| $1111Z]q_0$ | $11Z]q_1$ | $Z]q_1$ | ||
| $\vdash$ | $\vdash$ | |||
| $1111Z]q_1$ | $Z]q_2$ |
パズル.$0^n1^n$を受理するPDAを示せ。 答
PDAとCFGの等価性
本節では、PDAとCFGの等価性を示すため、最初にPDAの2つの受理方式(状態受理と$\varepsilon$受理)で言語の認識能力に差がないことを示し、続いてCFGに対し同じ言語を$\varepsilon$受理するPDAの構成と、$\varepsilon$受理PDAに対し、同じ言語を生成するCFGの構成を示す。状態受理と$\varepsilon$受理の等価性
定理.状態受理PDAと$\varepsilon$受理PDAの認識能力は等しい。
証明.PDA$M=(Q,\Sigma,\Gamma,\delta,q_0,Z,F)$に対し PDA$M'$を、スタックの底に記号$Z_0$を置いて$M$を模倣し、
・$M$の受理状態に達したら状態$p_\varepsilon$に遷移してスタックを空にし、
・スタックが$Z_0$($M$が空スタック)になったら受理状態$p_f$に遷移する
という方針で構成する。実際、 $M'=(Q',\Sigma,\Gamma',\delta',p_0,Z_0,\{p_f\}),\ Q'=Q\,\dot\cup\,\{p_0,p_\varepsilon,p_f\},\ \Gamma'=\Gamma\,\dot\cup\,\{Z_0\}\\ \delta'=\delta \,\dot\cup\,\{(p_0,\varepsilon,Z_0;ZZ_0,q_0)\}\\ \,\dot\cup\,\color{blue}{\{(q,\varepsilon,X;\varepsilon,p_\varepsilon)\mid q\in F\,\dot\cup\, \{p_\varepsilon\},\ X\in\Gamma'\}}\\ \,\dot\cup\,\color{purple}{\{(q,\varepsilon,Z_0;Z_0,p_f)\mid q\in Q\}}$
とおけば、$M$で$Z]q_0\vect{w}\VDASH{}{*} \alpha]q$
$\darrow{\rightarrow}{\leftarrow} M'$で $Z_0]p_0\vect{w}\vdash ZZ_0]q_0\vect{w}\VDASH{}{*} \alpha X_0]q \begin{cases} \color{blue}{\VDASH{}{*}{]}p_\varepsilon} & \color{blue}{q\in F のとき}\\ \color{purple}{\vdash Z_0]p_f} & \color{purple}{\alpha=\varepsilon のとき} \end{cases}$
となる。よって、$\mathcal{L}(M)=\mathcal{L}_\varepsilon(M')$、$\mathcal{L}_\varepsilon(M)=\mathcal{L}(M')$。
CFG$G$から$\varepsilon$受理PDA$M$への変換
CFG $G=(\Gamma,\Sigma,P,S)$ と $\vect{w}{\in}\Sigma^*,\ \gamma{\in} (\Sigma\dot\cup\Gamma)^*$に対し、最左導出で$S\overset{*}{\Rightarrow}\vect{w}\gamma \darrow{\rightarrow}{\leftarrow} S]q\vect{w} \VDASH{}{*} \gamma]q$ ――①
が成立つように、$\varepsilon$受理PDA $M:=(\{q\},\Sigma,\Sigma\,\dot\cup\,\Gamma, \delta_c\,\dot\cup\,\delta_d,q,S,\emptyset)$ の遷移を $\delta_c:=\{(q,a,a;\varepsilon,q)\mid a{\in}\Sigma\}
,\ \delta_d:=\{(q,\varepsilon,A;\alpha,q)\mid A{\to}\alpha{\in}P\}$ と定義する。
直感的に言えば、$M$は$\delta_d$の遷移を使ってスタック上で$G$の最左導出を模倣し、$\delta_c$の遷移を使って得られた終端文字列と入力とを照合する。実際、PDAのテープヘッドは左から順に読込むだけだから、任意の$\vect{v},\vect{w}\in\Sigma^*$に対し $S]q\vect{w} \VDASH{}{*} \gamma]q \darrow{\rightarrow}{\leftarrow} S]q\vect{w}\vect{v}\VDASH{}{*} \gamma]q\vect{v}$が成立つ。よって、CFG$G$の最左導出と$M$の動作列との間には、次の関係が成立つ。$\begin{cases} S\overset{*}\Rightarrow\vect{w}a\gamma
& \darrow{\rightarrow}{\leftarrow} S]q\vect{w}a\VDASH{}{*} a\gamma]qa\vdash \gamma]q\\
S\overset{*}\Rightarrow\vect{w}A\gamma\Rightarrow\vect{w}\alpha\gamma
& \darrow{\rightarrow}{\leftarrow} S]q\vect{w}\VDASH{}{*} A\gamma]q\vdash \alpha\gamma]q\end{cases}$
よって①式が成立ち、特に$\gamma=\varepsilon$とおけば、$\mathcal{L}(G)=\mathcal{L}_\varepsilon(M)$。
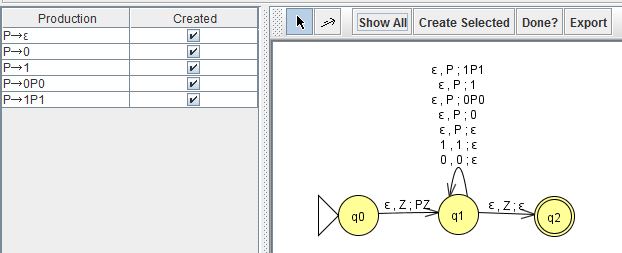 例.JFLAPによるCFG⇒PDA
例.JFLAPによるCFG⇒PDA
図の$q_0,q_2$は状態受理PDAに必要な状態で、$\varepsilon$受理PDAでは不要である。図のCFGの導出$P\Rightarrow 0P0\Rightarrow 010$に対し、右のPDAの受理動作列は以下のようになる。$Z]q_0010\vdash PZ]q_1010\vdash 0P0Z]q_1010\vdash P0Z]q_110\vdash 10Z]q_110\vdash 0Z]q_10\vdash Z]q_1\vdash ]q_2$
以下でPDAが認識する言語はCFGで生成されることを示すので、$\varepsilon$受理PDAの状態は1個で十分であることが言える。
CFG $G=(\Gamma,\Sigma,P,S)$ と $\vect{w}{\in}\Sigma^*,\ \gamma{\in} (\Sigma\dot\cup\Gamma)^*$に対し、
直感的に言えば、$M$は$\delta_d$の遷移を使ってスタック上で$G$の最左導出を模倣し、$\delta_c$の遷移を使って得られた終端文字列と入力とを照合する。実際、PDAのテープヘッドは左から順に読込むだけだから、任意の$\vect{v},\vect{w}\in\Sigma^*$に対し $S]q\vect{w} \VDASH{}{*} \gamma]q \darrow{\rightarrow}{\leftarrow} S]q\vect{w}\vect{v}\VDASH{}{*} \gamma]q\vect{v}$が成立つ。よって、CFG$G$の最左導出と$M$の動作列との間には、次の関係が成立つ。
図の$q_0,q_2$は状態受理PDAに必要な状態で、$\varepsilon$受理PDAでは不要である。図のCFGの導出$P\Rightarrow 0P0\Rightarrow 010$に対し、右のPDAの受理動作列は以下のようになる。$Z]q_0010\vdash PZ]q_1010\vdash 0P0Z]q_1010\vdash P0Z]q_110\vdash 10Z]q_110\vdash 0Z]q_10\vdash Z]q_1\vdash ]q_2$
以下でPDAが認識する言語はCFGで生成されることを示すので、$\varepsilon$受理PDAの状態は1個で十分であることが言える。
$\varepsilon$受理PDA$M$からCFG$G$への変換
PDA$M=(Q,\Sigma,\Gamma,\delta,q_0,Z,\emptyset),\ \alpha{\in}\Gamma^+,\ p,q{\in}Q$ に対し、$M$が$\alpha$を消費して状態$q$から$p$へ遷移する文字列の集合を$\| q\alpha p\|:=\{\vect{w}\mid \alpha]q\vect{w} \VDASH{}{*}{]}p\}$とおくと、$\mathcal{L}_\varepsilon(M)=\bigcup_{q\in Q}\|q_0Zq\|,\quad \|q\alpha\beta p\|=\bigcup_{r\in Q}\|q\alpha r\| \|r\beta p\|$
が成立ち、$(q,a,X;Y_1Y_2\cdots Y_k,p_k)\in\delta$ に対し、以下が言える。
$X]qa\vect{w}\vdash Y_1Y_2\cdots Y_k]p\vect{w}\VDASH{}{*}{}{]}p_k \darrow{\rightarrow}{\leftarrow}\\
\vect{w}\in \|pY_1Y_2\cdots Y_kp_k\|=\displaystyle\bigcup_{p_1,p_2,\dots,p_{k-1}\,\in Q}\|pY_1p_1\|\|p_1Y_2p_2\|\cdots\|p_{k-1}Y_kp_k\|$
よって、CFG$G:=(\Gamma',\Sigma,P,S),\ \Gamma':=\{S\}\,\dot\cup\,\{(qXp)\mid q,p\in Q,\ X\in \Gamma\}$
とし、$G$の規則を
$P:=\{S\to (q_0Zq)\mid q\in Q\}\,\dot\cup\,
\{(qXp_k)\to a(pY_1p_1)(p_1Y_2p_2)\cdots(p_{k-1}Y_kp_k)\mid\\
(q,a,X;Y_1Y_2\cdots Y_k,p)\in \delta,\ p_i\in Q,\ k\ge 1\}$
と定めると、$\|qXp\|=\mathcal{L}((qXp),G),\ \mathcal{L}_\varepsilon(M)=\mathcal{L}(G)$ が成立つ。
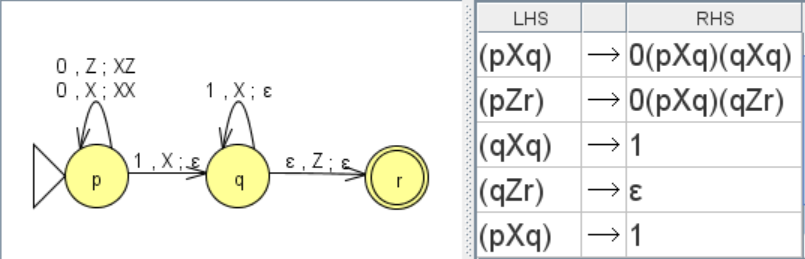 例.JFLAPによるPDA⇒CFG
例.JFLAPによるPDA⇒CFG
上記の構成は無駄な(終端記号列の生成に関わらない)非終端記号や規則を多量に作り出すが、図のCFGはそれらを除いてスリムにしている。図の、$0^n1^n$を受理するPDAの受理動作列の例と右のCFGの対応する導出例は以下のようになる。
$Z]p0011\vdash XZ]p011\vdash XXZ]p11\vdash XZ]q1\vdash Z]q\vdash ]r$
$S{\Rightarrow}(pZr){\Rightarrow}0(pXq)(qZr){\Rightarrow}00(pXq)(qXq)(qZr){\Rightarrow} 001(qXq)(qZr){\Rightarrow}0011(qZr){\Rightarrow}0011$
CFGで生成される言語はPDAが認識できることは示したので、CFGの規則の形は$A\to a\alpha,\ a\in\Sigma^?, \alpha\in\Gamma^*$の形に制限してもよいことが言える。
PDA$M=(Q,\Sigma,\Gamma,\delta,q_0,Z,\emptyset),\ \alpha{\in}\Gamma^+,\ p,q{\in}Q$ に対し、$M$が$\alpha$を消費して状態$q$から$p$へ遷移する文字列の集合を$\| q\alpha p\|:=\{\vect{w}\mid \alpha]q\vect{w} \VDASH{}{*}{]}p\}$とおくと、
 例.JFLAPによるPDA⇒CFG
例.JFLAPによるPDA⇒CFG上記の構成は無駄な(終端記号列の生成に関わらない)非終端記号や規則を多量に作り出すが、図のCFGはそれらを除いてスリムにしている。図の、$0^n1^n$を受理するPDAの受理動作列の例と右のCFGの対応する導出例は以下のようになる。
$Z]p0011\vdash XZ]p011\vdash XXZ]p11\vdash XZ]q1\vdash Z]q\vdash ]r$
$S{\Rightarrow}(pZr){\Rightarrow}0(pXq)(qZr){\Rightarrow}00(pXq)(qXq)(qZr){\Rightarrow} 001(qXq)(qZr){\Rightarrow}0011(qZr){\Rightarrow}0011$
CFGで生成される言語はPDAが認識できることは示したので、CFGの規則の形は$A\to a\alpha,\ a\in\Sigma^?, \alpha\in\Gamma^*$の形に制限してもよいことが言える。
文脈自由言語
定義. CFGで生成される(PDAで認識される)言語文脈自由言語(CFL, Context Free Language)という。定理. 1. CFLは和、連接、閉包、反転、準同型写像で閉じている
2. CFLは正則言語との共通部分で閉じている
証明.1.文脈自由文法で生成されることから、文脈自由言語が和、連接、閉包、反転、準同型写像で閉じていることが示せる。
2.状態受理PDAで認識されることより、CFLが正則言語との共通部分で閉じていることが示せる。PDA$M=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)$とDFA$N=(R,\Sigma,\eta,r_0,H)$に対し
直感的には、$M{\times}N$は$M$と$N$の動作を同時並行的に模倣する。この手法をDFA$M,\ N$に対して適用すれば、$\mathcal{L}(M)\cap\mathcal{L}(N)$を認識するDFAを(直接)構成できる。
問. 定理の1.を示せ。
反復補題
ある言語がCFLでないことを示すには、次の補題が有用である。
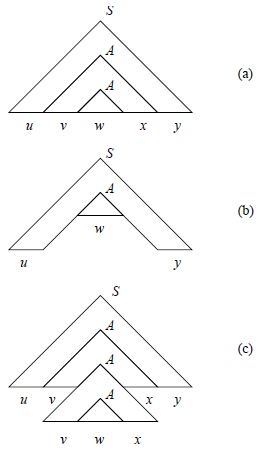

反復補題.CFL$L\ (\subseteq\Sigma^*)$ に対しある正整数$p$が存在して、$L$の$p$より長い文字列$\vect{z}$は$\vect{z}=\vect{uvwxy}$と書けて、$\vect{vx}\ne\varepsilon,\ |\vect{vwx}|\le p$、任意の$k$に対し$\vect{uv}^k\vect{wx}^k\vect{y}\in L$が成立つ。
証明.$L$を生成するCFGにおける$\vect{z}=\vect{uvwxy}$の導出木は、$\vect{z}$が十分長ければ途中で同じ非終端記号が(異なる位置に)現れる路を持ち(鳩ノ巣原理、上図)、その部分の導出を反復できる(右図)。ここで、$\vect{vx}=\varepsilon$ならばその間の路を短絡しても導出する文字列は不変なので、$\vect{vx}\ne\varepsilon$とできる。$p$は構文木がそのような路を持つ最短の語の長さとする。
応用例.$\{0^n1^n2^n|n\in\mathbb{N}\}$はCFLでない。
証明.CFLと仮定し$\vect{z}=0^p1^p2^p$に対し反復補題を適用すれば、$|\vect{vwx}|\le p$より、$\vect{vx}\not\in 0^+1^+2^+$。よって矛盾。即ち、CFLが3か所同期して増えることはない。
定理. CFLは共通部分、補集合で閉じていない
証明.$\{0^n1^n2^n|n\in\mathbb{N}\}=\{0^n1^n|n\in\mathbb{N}\}\{2\}^*\cap\{0\}^*\{1^n2^n|n\in\mathbb{N}\}$ よりCFLは共通部分で閉じていない。和集合では閉じているので、補集合で閉じていない。
問.$\{\vect{ww}|\vect{w}{\in}\{0,1\}^*\}$ はCFLでないことを示せ。
ある言語がCFLでないことを示すには、次の補題が有用である。
反復補題.CFL$L\ (\subseteq\Sigma^*)$ に対しある正整数$p$が存在して、$L$の$p$より長い文字列$\vect{z}$は$\vect{z}=\vect{uvwxy}$と書けて、$\vect{vx}\ne\varepsilon,\ |\vect{vwx}|\le p$、任意の$k$に対し$\vect{uv}^k\vect{wx}^k\vect{y}\in L$が成立つ。
証明.$L$を生成するCFGにおける$\vect{z}=\vect{uvwxy}$の導出木は、$\vect{z}$が十分長ければ途中で同じ非終端記号が(異なる位置に)現れる路を持ち(鳩ノ巣原理、上図)、その部分の導出を反復できる(右図)。ここで、$\vect{vx}=\varepsilon$ならばその間の路を短絡しても導出する文字列は不変なので、$\vect{vx}\ne\varepsilon$とできる。$p$は構文木がそのような路を持つ最短の語の長さとする。
応用例.$\{0^n1^n2^n|n\in\mathbb{N}\}$はCFLでない。
証明.CFLと仮定し$\vect{z}=0^p1^p2^p$に対し反復補題を適用すれば、$|\vect{vwx}|\le p$より、$\vect{vx}\not\in 0^+1^+2^+$。よって矛盾。即ち、CFLが3か所同期して増えることはない。
定理. CFLは共通部分、補集合で閉じていない
証明.$\{0^n1^n2^n|n\in\mathbb{N}\}=\{0^n1^n|n\in\mathbb{N}\}\{2\}^*\cap\{0\}^*\{1^n2^n|n\in\mathbb{N}\}$ よりCFLは共通部分で閉じていない。和集合では閉じているので、補集合で閉じていない。
問.$\{\vect{ww}|\vect{w}{\in}\{0,1\}^*\}$ はCFLでないことを示せ。
Parikh写像
文字列中の文字出現数を数えるParikh写像によるCFLの像は準線形集合であり、準線形集合は正則集合のParikh写像の像になることを示そう。
定義.$\Sigma{=}\{a_1,a_2,\dots.a_n\}$上のParikh写像$\psi:\Sigma^*{\to}{}_n[\mathbb{N}]$を帰納的に$\psi(\varepsilon){:=}\vect{0},$ $\psi(\vect{w}a_i){:=}\psi(\vect{w}){+}\vect{e}_i$で定義する。
定理.準線形集合は、正則集合のParikh写像$\psi$による像として表される。
証明.$\psi^{-1}(\vect{p})$は正則(有限)集合で$\vect{c}{+}\mathbb{N}[\vect{p}_i]^m=\psi\left(\psi^{-1}(\vect{c})\left(\bigcup_{i=1}^n \psi^{-1}(\vect{p}_i)\right)^*\right)$。準線形集合は線型集合$\vect{c}{+}\mathbb{N}[\vect{p}_i]^m$の有限和だから定理が成立つ。
定理.CFL$L$のParikh写像$\psi$による像$\psi(L)$は準線形集合である。
略証.CFG$G=(\Gamma,\Sigma,P,S)$の導出木の部分木$t$を考え、$t$の根(のラベル、以下同様)を$\dot{t}$、葉を順に並べた列を$\underline{t}$と表す。反復補題で反復された部分木、$\underline{t}\in\Sigma^*\dot{t}\Sigma^* $である木を反復木と呼ぼう。内点(葉でない点)がすべて異なる反復木の集合$\mathcal{P}$は有限集合である。$t$の頂点にある非終端記号の集合を$\Gamma(t)$と表す。完了導出木$s,t$に対し$s\precsim t$を、$\Gamma(s){=}\Gamma(t)$かつ$s$に反復木を繰返し埋め込んで$t$が得られることと定義すれば、$\precsim$に関する極小木$s$は、内点がすべて異なる完了導出木への$\Gamma(s)$を真に増やす埋込のみで構成され、極小木の集合$\mathcal{C}$は有限集合である。$t{\in}\mathcal{C}$に$\mathcal{Q}{\subseteq}\mathcal{P}$の反復木を繰返し埋込んで得られる木の集合を$t\langle\mathcal{Q}\rangle^*$と表せば、$G$の完了導出木の集合は$\bigcup_{t\in \mathcal{C}}t\langle\mathcal{P}\cap\{s\mid \Gamma(s){\subseteq}\Gamma(t)\}\rangle^*$と書け、Parikh写像を導出木中の終端記号のカウントに拡張適用すれば、定理が成立つ。
これらの定理より、Parikh写像を通してみれば文脈自由言語と正則言語は一致してともに準線形集合になり、一文字上の文脈自由言語と正則言語のクラスは一致する。
文字列中の文字出現数を数えるParikh写像によるCFLの像は準線形集合であり、準線形集合は正則集合のParikh写像の像になることを示そう。
定義.$\Sigma{=}\{a_1,a_2,\dots.a_n\}$上のParikh写像$\psi:\Sigma^*{\to}{}_n[\mathbb{N}]$を帰納的に$\psi(\varepsilon){:=}\vect{0},$ $\psi(\vect{w}a_i){:=}\psi(\vect{w}){+}\vect{e}_i$で定義する。
定理.準線形集合は、正則集合のParikh写像$\psi$による像として表される。
証明.$\psi^{-1}(\vect{p})$は正則(有限)集合で$\vect{c}{+}\mathbb{N}[\vect{p}_i]^m=\psi\left(\psi^{-1}(\vect{c})\left(\bigcup_{i=1}^n \psi^{-1}(\vect{p}_i)\right)^*\right)$。準線形集合は線型集合$\vect{c}{+}\mathbb{N}[\vect{p}_i]^m$の有限和だから定理が成立つ。
定理.CFL$L$のParikh写像$\psi$による像$\psi(L)$は準線形集合である。
略証.CFG$G=(\Gamma,\Sigma,P,S)$の導出木の部分木$t$を考え、$t$の根(のラベル、以下同様)を$\dot{t}$、葉を順に並べた列を$\underline{t}$と表す。反復補題で反復された部分木、$\underline{t}\in\Sigma^*\dot{t}\Sigma^* $である木を反復木と呼ぼう。内点(葉でない点)がすべて異なる反復木の集合$\mathcal{P}$は有限集合である。$t$の頂点にある非終端記号の集合を$\Gamma(t)$と表す。完了導出木$s,t$に対し$s\precsim t$を、$\Gamma(s){=}\Gamma(t)$かつ$s$に反復木を繰返し埋め込んで$t$が得られることと定義すれば、$\precsim$に関する極小木$s$は、内点がすべて異なる完了導出木への$\Gamma(s)$を真に増やす埋込のみで構成され、極小木の集合$\mathcal{C}$は有限集合である。$t{\in}\mathcal{C}$に$\mathcal{Q}{\subseteq}\mathcal{P}$の反復木を繰返し埋込んで得られる木の集合を$t\langle\mathcal{Q}\rangle^*$と表せば、$G$の完了導出木の集合は$\bigcup_{t\in \mathcal{C}}t\langle\mathcal{P}\cap\{s\mid \Gamma(s){\subseteq}\Gamma(t)\}\rangle^*$と書け、Parikh写像を導出木中の終端記号のカウントに拡張適用すれば、定理が成立つ。
これらの定理より、Parikh写像を通してみれば文脈自由言語と正則言語は一致してともに準線形集合になり、一文字上の文脈自由言語と正則言語のクラスは一致する。
CFLの特徴づけ
アルファベット$\Delta$に対し、$\Delta_{[\,]}:=\{[_d,]_d\mid d\in \Delta\}$とおき、CFG$G_D=(\{S\},\Delta_{[\,]},\{S\to\varepsilon\}\cup\{S\to [_d S ]_d S\mid d{\in}\Delta\},S)$が生成する言語$D_\Delta:=\mathcal{L}(G_\Delta)$を$\Delta_{[\,]}$上のDyck言語という。$D_\Delta$は括弧のバランス(対応)のとれた列の集合である。
定理.任意のCFLはDyck言語と正則言語の共通部分の準同型写像の像になる。
証明.CFL$L$を受理する1状態$\varepsilon$受理PDAを$M=(\{q\},\Sigma,\Gamma,\delta,q,Z, \emptyset)$とし、(必要なら記号を置き換え)$\Sigma\cap\Gamma=\emptyset$とする。$\Sigma_{[\,]}\dot\cup\Gamma_{[\,]}$上の正規言語を$R:=\{[_{Z}\}\{[_a\,]_a\,]_X\,[_{X_k}\cdots[_{X_2}\,[_{X_1}\ \mid (q,a,X;X_1X_2\cdots X_k,q){\in}\delta,\ 但し[_\varepsilon=]_\varepsilon{=}\varepsilon\}^+$
とおき、準同型写像$h:\Sigma_{[\,]}\dot\cup\Gamma_{[\,]}\to \Sigma$を$h([_a):=a,\ h(]_a)=h([_X)=h(]_X):=\varepsilon$で定めれば、$L=h(D_{\Sigma\dot\cup\Gamma}\cap R)$が成立つ。
実際、$[_X$をスタックに記号$X$を積む動作、$]_X$をスタックから記号$X$を取出す動作と解釈することによって、 $\alpha\in D_{\Sigma\dot\cup\Gamma}\cap R$は入力$h(\alpha)$が引き起こす$M$の動作列と解釈できる。$\alpha\in R$は$\alpha$が$M$の動作を並べた列であることを保証し、$\alpha\in D_{\Sigma\dot\cup\Gamma}$は$\alpha$が正当なスタック操作列であることを保証する。
定理.前節の$0^n1^n$を受理するPDAの動作列 $Z]p0011\vdash XZ]p011\vdash XXZ]p11\vdash XZ]q1\vdash Z]q\vdash ]r$ に対応する $D_{\Sigma\dot\cup\Gamma}\cap R $の文字列は $[_Z\cdot [_0]_0[_X\cdot [_0]_0[_X\cdot [_1]_1]_X\cdot [_1]_1]_X\cdot ]_Z$ となる。($\cdot$は連接演算を表す)
定理より、文脈自由言語は本質的に正則言語に括弧構造(による制御)を付加したものと見なせる。
アルファベット$\Delta$に対し、$\Delta_{[\,]}:=\{[_d,]_d\mid d\in \Delta\}$とおき、CFG$G_D=(\{S\},\Delta_{[\,]},\{S\to\varepsilon\}\cup\{S\to [_d S ]_d S\mid d{\in}\Delta\},S)$が生成する言語$D_\Delta:=\mathcal{L}(G_\Delta)$を$\Delta_{[\,]}$上のDyck言語という。$D_\Delta$は括弧のバランス(対応)のとれた列の集合である。
定理.任意のCFLはDyck言語と正則言語の共通部分の準同型写像の像になる。
証明.CFL$L$を受理する1状態$\varepsilon$受理PDAを$M=(\{q\},\Sigma,\Gamma,\delta,q,Z, \emptyset)$とし、(必要なら記号を置き換え)$\Sigma\cap\Gamma=\emptyset$とする。$\Sigma_{[\,]}\dot\cup\Gamma_{[\,]}$上の正規言語を
実際、$[_X$をスタックに記号$X$を積む動作、$]_X$をスタックから記号$X$を取出す動作と解釈することによって、 $\alpha\in D_{\Sigma\dot\cup\Gamma}\cap R$は入力$h(\alpha)$が引き起こす$M$の動作列と解釈できる。$\alpha\in R$は$\alpha$が$M$の動作を並べた列であることを保証し、$\alpha\in D_{\Sigma\dot\cup\Gamma}$は$\alpha$が正当なスタック操作列であることを保証する。
定理.前節の$0^n1^n$を受理するPDAの動作列 $Z]p0011\vdash XZ]p011\vdash XXZ]p11\vdash XZ]q1\vdash Z]q\vdash ]r$ に対応する $D_{\Sigma\dot\cup\Gamma}\cap R $の文字列は $[_Z\cdot [_0]_0[_X\cdot [_0]_0[_X\cdot [_1]_1]_X\cdot [_1]_1]_X\cdot ]_Z$ となる。($\cdot$は連接演算を表す)
定理より、文脈自由言語は本質的に正則言語に括弧構造(による制御)を付加したものと見なせる。
決定性PDA(DPDA)
① $|\delta(q,a,X)|\le 1$
② $\delta(q,\varepsilon,X){\ne}\emptyset\wedge a{\ne}\varepsilon \drarrow \delta(q,a,X){=}\emptyset$
この条件を満たすと、入力に対する動作列は高々1つ(決定性)になる。前節でPDAから構成したCFGの最左導出列はPDAの動作列と1対1に対応するから、DPDAから構成されるCFGはあいまいでない。したがってあいまいなCFLはDPDAで受理できない。
例.右上図は$\{wcw^R\mid w\in\{0,1\}^*\}$を認識するDPDAである。
定理.決定性文脈自由言語(DPDAで受理される言語)のクラスは補集合演算で閉じているが和集合、積集合で閉じていない。
問.この定理を証明せよ。