3章　正規表現の応用

この章の目標

正規(正則)表現は、検索・置換・テキスト処理等、応用範囲が広く、コンピュータ上で正規表現を便利に入力できるよう、様々な記法が用意されている。それらを用いた表現を本節では慣習に基づき正規表現と呼ぶ。
　正規表現の記法には、処理系によって若干の揺れがあるが、本節では標準的なものを紹介する。

本節ではテキスト処理の観点から
・正規表現の記法を学び、
・正規表現による検索について紹介し、
・正規表現による置換について紹介し、
・字句解析プログラム生成ツールLEXのアイディアを紹介する。

言語の方程式

　言語の(右線型)方程式を考えてみよう。

定理．言語の方程式$X=AX{\cup}B,\ A,B{\subseteq}\Sigma^*$に対し
1. $A^*B$は(包含関係での)最小解である。
2. $\varepsilon{\not\in}A \drarrow A^*B$は唯一の解である。
証明．1. $A(A^*B){\cup}B=A^+B{\cup}A^0B=A^*B$より$X=A^*B$は解である。$X{\supseteq}AX \drarrow X{\supseteq}AX{\supseteq}A^2X{\supseteq}\cdots \drarrow X{=}A^*X$ より $X{=}AX{\cup}B \drarrow X{=}A^*X{\supseteq}A^*B$。
2. $X$が解なら$A^nX{-}A^*B=A^n(AX{\cup}B){-}A^*B=A^{n+1}X{-}A^*B,\ n{=}0,1,\dots$。よって、$\vect{w}\in X{-}A^*B=A^{|\vect{w}|+1}X{-}A^*B \drarrow \varepsilon{\in}A$。

　連立方程式$X_i=\bigcup_{j=1}^n A_{ij}X_j \cup B_i,\ i=1,2,\dots,n$の最小解を求める一般的な手順は、$X_1=A_{11}X_1\cup\left(\bigcup_{j=2}^nA_{1j}X_j \cup B_1\right) =A_{11}^*\left(\bigcup_{j=2}^nA_{1j}X_j \cup B_1\right)$を代入して、 $X_i=\bigcup_{j=2}^n(A_{i1}A_{11}^*A_{1j}\cup A_{ij})X_j \cup (A_{i1}A_{11}^*B_1\cup B_i),\ i=2,\dots,n$を得る。これを繰返して$X_n$を求めたら、そこから逆に$X_{n-1},\dots,X_2,X_1$が求まる。よって、連立方程式$X_i=\bigcup_{j=1}^n A_{ij}X_j \cup B_i,\ i=1,2,\dots,n$ の最小解は、$A_{ij},B_i$から$\cup,\ \cdot,\ ^*$ を使って表される。実際の求解手順では、数の連立方程式と同様の工夫が可能だが、求まる表現は手順により(表す言語は同じだが)異なる事がある。

例．$\{\vect{w}\}を\vect{w}$で表す。連立方程式$\begin{cases}S=0S{\cup}1A　\\A=0S{\cup}1A{\cup} \varepsilon　\end{cases}$ の最小解の$S$を求めよう。

$S=0^*1A$より$A=1A{\cup}00^*1A{\cup}\varepsilon=(1{\cup}00^*1)^*$。$S=0^*1(1{\cup}00^*1)^*$。
$A=1^*(0S{\cup}\varepsilon)$より$S=0S{\cup}11^*(0S{\cup}\varepsilon)=(0{\cup}11^*0)S{\cup}11^*=(0{\cup}11^*0)^*11^*$。
$A=(0S{\cup}1A){\cup}\varepsilon=S{\cup}\varepsilon$。よって$S=0S{\cup}1S{\cup}1=(0{\cup}1)^*1$。

問．方程式$X=XA\cup B$の最小解は$BA^*$であることを示せ。

正規(正則)表現

　正則文法$G=(\Sigma,\{X_1,X_2,\dots,X_n\},P,X_1)$に対し $B_i{:=}\{\vect{w}\mid X_i{\to}\vect{w}{\in}P\},\ A_{ij}{:=}\{\vect{w}\mid X_i{\to}\vect{w}X_j{\in}P\}$ とおく。このとき$L_i=\mathcal{L}(X_i,G),\ 1\le i \le n$は、同時帰納的に
$\vect{w}{\in}B_i \drarrow \vect{w}{\in}L_i,\quad \vect{w}{\in}A_{ij} \wedge \vect{v}{\in}L_j\drarrow \vect{wv}{\in}L_i$ で定義できるから、$B_i\subseteq L_i \wedge \bigcup_{j=1}^nA_{ij}L_j\subseteq L_i$ を満たす最小集合で、前節の議論より、連立方程式$X_i=\bigcup_{j=1}^n A_{ij}X_j \cup B_i$の最小解である。
　以上を踏まえて、文字列の単集合$\{\vect{w}\}$から$\cup,\ \cdot,\ ^*$で構成される表現を正規(正則)表現という。正確には($\Sigma$)の)正規表現は帰納的に、

$\vect{w}{\in}\Sigma^* \drarrow \{\vect{w}\}$は正規表現
$\alpha,\beta$が正規表現${}\drarrow \alpha\cup\beta,\alpha\beta,\alpha^*$も$\Sigma$上の正規表現

で定義される。

正則言語と正規表現
定理．$L$が正則言語${}\darrow{\rightarrow}{\leftarrow} L$は正規表現で表される
$\dlarrow$）$\{\vect{w}\}$は正則言語で、正則言語は$\cup,\ \cdot,\ ^*$で閉じているから明らか
$\drarrow$）正則文法から導かれる連立方程式の係数$A_{ij}, B_i$は文字列の単集合の和で表されるので、前節の議論から明らか。

問．3で割り切れる2進数の集合について

認識する有限オートマトンを求めよ　答
生成する正則文法を求めよ
正規表現を求めよ（文字列に対する$[\{,\}$は省略してよい）

　正規表現は本章で紹介するように、コンピュータによるテキスト処理に広く応用されているが、その際は、以下に示す多くの便宜的表記法が用いられる。また、正規表現は、文字列パターンの記述と捉えることができ、文字列$w$が正規表現$\alpha$が表す正則言語に属すとき、$w$は$\alpha$に合致するという。

基本

記法	説明
文字列	文字列$\vect{w}$は正則言語$\{\vect{w}\}$を表し、文字列$\vect{w}$と合致
連接	正規表現を続けて書けば、それらを続けた文字列と合致
\|	和言語(または)。どちらかのパターンと合致すれば合致。
*	直前の文字(文字列)集合の0回以上の繰り返しと合致

例．正則言語$(\{0\}\cup\{1\})^*\{01\}$は (0|1)*01 と表わされる。

繰返し

記法	説明	使用例
+	1回以上の繰り返し	12+ → 12、122、・・・と合致 12+＝122*
?	0,1回の繰り返し	12? → 1、12 と合致 12?＝1\|12
{n}	n回繰り返し	(ab){3} → abababに合致
{n, }	n回以上繰り返し	a{3,} →aaa、aaaa、…に合致
{m,n}	m～n回繰り返し	a{3,5} →aaa、aaaa、aaaaaに合致

合致する文字列は、通常はパターンに適合する最長の文字列(最長合致)であるが、*や+の直後に"?"を付けると最短合致となる。
　　12+ →1222222222 に対し10桁目の1222222222までと合致
　　12+? →1222222222 に対し2桁目の12までと合致

文字の集合：1文字指定する

記法	説明	使用例
.	改行を除く任意の1文字	windows.. windowsの後に2文字続く列
[ ]	[ ] 内の文字のどれか	[ab]＝a\|b
-	文字の区間。[ ] 内で用いる	[a-z]＝a\|b\|・・・\|z 英小文字全て [０-９]＝０\|１\|・・・\|９全角数字 [0-9A-Z] 英大文字か数字
^	否定。[ ] 内で用いる	[^a-z] 英小文字以外全て

特殊な意味を持つ表現

記法	説明	使用例
^	行頭	^abc →行頭にある abc と合致
$	行末	abc$ →行末にある abc と合致

記法	説明
\w	アルファベット、数字、下線
\d	数字
\s	空白(スペース、タブ、改行)
\b	単語の区切り
\n	改行
\r	リターン(復帰)
\t	タブ

記法	説明
\W	アルファベット、数字、下線以外
\D	数字以外。[^0-9] と同じ
\S	空白文字以外
\B	単語の区切り以外

正規表現の応用

正規表現による検索
　正規表現による検索機能の応用例を紹介しよう。ファイル中からパターンに一致する箇所やパターンを含む行を取り出す grep が有名だが、SKELLでは学習用データベースから合致するパターンを含む英文とその頻度を表示する帰納【Examples】があり、生きた英語を学習できる。(Skellには英語学習に特化した更に有用な多くの機能がある)
　さらに、データベースと正規表現をうまく組み合わせる事により、文書・文献の特徴を抽出し、例えば著者の異同や時代の推定、思想と文体との関係等を分析することも可能になる。その意味で、正規表現検索は文書の処理・解析のための重要なツールになっている。

実験．SKELL

Search Word欄に色々な正規表現を入れて【Examples】を探してみよう
「take an appointment」と「make an appointment」の出現頻度を比べよ

※ SKELLでは、動詞の活用形を自動的に含めたり、正規表現で\sが使えず実際の空白で表す等若干異なる。

問．正規表現 (for|in|on|to|with) [a-z]+ing (for|in|of|on|to|with) は何を意味するか考え、SKELLで試してみよ。

正規表現による検索と置換
　正規表現の検索機能に加えて、パターンに合致した文字列を別の文字列に置換する機能を紹介しよう。正規表現の置換は単なる文字列の置換に留まらず、指定パターンに合致した文字列を利用して置換文字列を指定できる。具体的には、$\$n$で、正規表現の$n$番目の括弧対で括られた部分に合致した文字列を表す。
　次ページのアプリ(Java Scriptで実装)で検索文字列や置換文字列を指定して[検索]、[置換]を押すと結果が下の欄に表示される。検索欄には正規表現を、置換欄には$n(nは番号)を含む文字列を指定する。

問．1～5の正規表現を求め検索・置換せよ。

3桁の数字
3000未満の非負整数
aで始まりaで終わる6文字以下の英小文字列
全角数字０～９で始まり句点。で終わる行
英字の姓と名を入れ替えよ
行頭の空白を削除せよ

LEX:検索＋アクション
前節の検索＋置換から進んで、検索文字列に対し実行するアクションを指定っできる仕組みを紹介しよう。字句解析プログラム生成ツールであるLexでは、正規表現で指定された文字列ｚに対する一般的な処理が記述でき、その応用領域は、コンパイラの(字句解析部)の作成、自然言語処理や文書整形まで幅広い。
　Lexの規則は　正規表現アクション(合致文字列に対する処理);
の形をしており、合致する正規表現がない文字列はそのまま出力される。

用途例１．テキスト処理（単独で）
　[ ]+$ ; 行の末尾の空白列を消去する(空列に置き換える)するLex規則

用途例２．字句解析プログラム生成系（第5章のyaccと組み合わせて）
プログラム中の予約語、名前、数、演算記号等を切り分け分類するLex規則群


正規表現	アクション
else	return(ELSE);
[A-Za-z][A-Za-z0-9]*	{見つけた名前を記号表に登録;return(ID);}
[+-]?(0\|[1-9][0-9]*)	{表す整数値を定数表に登録;return(NUM);}
>=	return(GE);
=	return(EQ);
・・・	・・・

この機能を組み込んだプログラミング言語としてAWKが知られている。

論理式と正則言語

本節では、論理式で正則言語を記述することを考えよう。基本の述語を「文字列$\vect{w}\;({\in}\Sigma^*)$の$x$番目の文字は$a$である」としこれを$\vect{w}(x,a)$と表す(文字は0番目から始める)。主に考慮すべき点は、

$\vect{w}(x,a):\mathbb{N}{\times}\Sigma{\to}\{\top,\bot\}$とするのが自然^❶だが、$\vect{w}$は有限長である事
論理式はDFAの動作を記述できる能力がある事
非正則言語が記述できないようにする事

1.記号$\square\not\in\Sigma$を使って$\vect{w}\square^*$の要素を互いに同一視し、必要なら文字列をいくらでも長くできるようにする。$\vect{w}(x,\square) \leftrightarrows \bigwedge_{a\in\Sigma}\neg\vect{w}(x,a)$とする。
2.DFA$M=(Q,\Sigma,\delta,q_0,F)$に対し、以下が成立つ。($\vect{q}$は$M$の状態列) $\vect{w}\in\mathcal{L}(M) \leftrightarrows \exists\vect{q}\forall x \left((x{=}0{\to}\vect{q}(x,q_0))\wedge \left(\bigvee_{(p,a,q)\in \delta}(\vect{q}(x,p){\wedge}\vect{w}(x,a){\wedge}\vect{q}(x{+}1,q))\\ \vee \bigvee_{q \in F} (\vect{q}(x,q){\wedge}\vect{w}(x,\square){\wedge}\vect{q}(x{+}1,\square) %\vee \vect{q}(x,\square){\wedge}\vect{w}(x,\square) )\right)\right)$ 3.変数$x,y$に対し和($+$)や定数倍を許すと表現力は正則言語を超える。 $\exists n\;\vect{w}{=}a^nb^n \leftrightarrows \exists y\forall x\left(0{\le}x{\lt}y{\to}\vect{w}(x,a)\wedge y{\le}x{\lt}2y{\to}\vect{w}(x,b))\wedge 2y{\le}x{\to}\vect{w}(x,\square)\right)$

❶ このテキストの範囲を超えるが、$\Sigma$上長さ無限の$\omega$文字列$\vect{w}:\mathbb{N}{\to}\Sigma$から成る$\omega$正則言語が研究されている。

　以上の考察を踏まえて、論理体系$\mathfrak{R}$で使える記号と論理式を次で定める。

定数$k\in\mathbb{N}$と、変数$x,y$、述語$\vect{v}$、文字$a$に対し、$x{=}k,\ x{=}y{+}k,\ x\lt y,\ \vect{v}(x,a)$は論理式である。
$\varphi,\psi$が$\mathfrak{R}$の論理式ならば、$\varphi{\vee}\psi,\neg\varphi,\exists x\,\varphi, \exists\vect{v}\,\varphi$は論理式である。

$\exists x\,\varphi, \exists\vect{v}\,\varphi$において$x, \vect{v}$は束縛されているといい、束縛されていない変数・述語は自由であるという。

　以下、略記 $\vect{v}(t,a):\equiv\exists x\ x{=}t{\wedge}\vect{v}(x,a)\ (t{=}k または t{=}y{+}k),$ $\varphi{\to}\psi:\equiv \neg\varphi{\vee}\psi,$ $\varphi{\wedge}\psi:\equiv \neg(\neg\varphi{\vee}\neg\psi),$ $\forall x\varphi:\equiv \neg\exists x\ \neg\varphi,$ $\forall\vect{v}\,\varphi:\equiv \neg\exists\vect{v}\,\neg\varphi$を用いる。
　論理体系$\mathfrak{R}$の変数$x_1,\dots,x_m$と述語$\vect{v}_1,\dots,\vect{v}_n$を自由に持つ論理式に対する解釈(言語)を定めるために、$\vect{2}:=\{0,1\}$とし、アルファベット $\Gamma:=\{\langle d_1,\dots,d_m,a_1,\dots,a_n,\rangle\mid d_i{\in}\vect{2}, 1{\le}i{\le}m,\ a_j{\in}\Sigma_j{\dot\cup}\{\square\},1{\le}j{\le}n\}$ とおく。$\Gamma$の第$i$成分を取出す射影$\pi_i:\langle c_1,\dots,c_{m+n}\rangle \mapsto c_i$は準同型写像$\pi_i:\Gamma^*{\to}\pi_i(\Gamma)^*{=} \begin{cases} \vect{2}^* & 1{\le}i{\le}m\\ (\Sigma_{i-m}{\cup}\{\square\})^* & m{+}1{\le}i{\le}m{+}n \end{cases}$を定める。第$i,j$成分を取出す射影$\pi_{i,j}:\langle c_1,\dots,c_{m+n}\rangle\mapsto \langle c_i,c_j\rangle \equiv {c_i\atop c_j}$ や第$i$成分を取り除く射影$\pi_{\bar i}:\langle c_1,\dots,c_{m+n}\rangle \mapsto \langle c_1,\dots,c_{i-1},c_{i+1},\dots, c_{m+n}\rangle$についても同様とする。
　正則言語は集合和と集合差、準同型写像とその逆像、で閉じているから$\mathcal{R}$の論理式の解釈が、正則言語で与えられる。実際、正則言語 $\mathcal{U}(\Gamma):=\{\vect{\alpha} \mid 1{\le}i{\le}m {\drarrow} \pi_i(\vect{\alpha}){\in}0^*10^*,\ m{+}1{\le}i{\le}m{+}n {\drarrow} \pi_i(\vect{\alpha}){\in}\Sigma_{i-m}^*\square^+\}$ を解釈世界と見做し、論理式に対する解釈(正則言語)を以下で定義できる。
　　$\mathcal{L}(\Gamma;x_i{=}k):=\left\{\vect{\alpha}{\in}\mathcal{U}(\Gamma) \left| \pi_{i}(\vect{\alpha}){\in}0^k10^*\right.\right\},\\ \mathcal{L}(\Gamma;x_i{=}x_j):=\left\{\vect{\alpha}{\in}\mathcal{U}(\Gamma) \left| \pi_{i,j}(\vect{\alpha}){\in}\left({0\atop 0}\right)^*{1\atop 1}\left({0\atop 0}\right)^*\right.\right\},\\ \mathcal{L}(\Gamma;x_j{=}x_i{+}k):=\left\{\vect{\alpha}{\in}\mathcal{U}(\Gamma) \left| \pi_{i,j}(\vect{\alpha}){\in}\left({0\atop 0}\right)^*{1\atop 0}\left({0\atop 0}\right)^{k-1}{0\atop 1}\left({0\atop 0}\right)^*\right.\right\},\ k{\ge}1\\ \mathcal{L}(\Gamma;x_i{\lt}x_j):=\left\{\vect{\alpha}{\in}\mathcal{U}(\Gamma) \left| \pi_{i,j}(\vect{\alpha}){\in}\left({0\atop 0}\right)^*{1\atop 0}\left({0\atop 0}\right)^*{0\atop 1}\left({0\atop 0}\right)^*\right.\right\},\\ \mathcal{L}(\Gamma;\vect{v}_j(x_i,a)):=\left\{\vect{\alpha}{\in}\mathcal{U}(\Gamma) \left| \pi_{i,m+j}(\vect{\alpha}){\in}\left({0\atop\Sigma_j}\right)^*{1\atop a}\left({0\atop\Sigma_j}\right)^* \left({0\atop\square}\right)^+\right.\right\}$
　　　　（$\vect{v}_j{\in}\Sigma_j \square^+,\ {0\atop\Sigma_j}:=\{{0\atop a}\mid a{\in}\Sigma_j\}$とする。）
　$\mathfrak{R}$の論理式$\varphi,\ \psi$に対し、
　　$\mathcal{L}(\Gamma;\varphi \vee \psi):=\mathcal{L}(\Gamma;\varphi)\cup \mathcal{L}(\Gamma;\psi),\ \mathcal{L}(\Gamma;\neg \varphi):=\mathcal{U}(\Gamma)-\mathcal{L}(\Gamma;\varphi)$
　　$\mathcal{L}(\pi_{\bar i}(\Gamma);\exists x_i\varphi):=\pi_{\bar i}(\mathcal{L}(\Gamma;\varphi)),\ \mathcal{L}(\pi_\overline{m+j}(\Gamma);\exists \vect{v}_j\varphi):=\pi_\overline{m+j}(\mathcal{L}(\Gamma;\varphi))$

　以上の議論により、自由な述語$\vect{v}$を持つ$\mathfrak{R}$の論理式$\varphi(\vect{v})$が定める言語 $\mathcal{L}(\varphi(\vect{v})):=\{\vect{w}\in\Sigma^*\mid \vect{w}\square^*\cap \mathcal{L}(\Sigma;\varphi(\vect{v}))\ne \emptyset\}$は正則言語であり、逆も成立つ。
注2．本来$\mathcal{L}(\Sigma{\cup}\square;\varphi(\vect{v}))$と書くべきであるが、$\square$は省略する。

　自由変数のない論理式を命題という。前節の議論により、次の定理が成立つ。
定理．論理体系$\mathfrak{R}$の命題の真偽は判定可能である。

注3．$\vect{w}{\in}\vect{2}^*$は$\mathbb{N}$の有限集合$\{x\mid \vect{w}(x,1)\}$と見做せるから、論理体系$\mathfrak{R}$の(文字列)述語を$\mathbb{N}$の有限集合とした論理体系は真偽が判定可能である。さらに注1に従って、述語を$\mathbb{N}$の部分集合とした論理体系も、真偽が判定可能であることが示せる。

　$\mathfrak{R}$における$述語$と$\forall x$の取扱い(意味)を見るために、次の例1,2.を考えよう。

例１．$\forall x_1\,\vect{w}(x_1,\square) \equiv\neg\exists x_1\,\neg\vect{w}(x_1,\square)$に対し、 $\mathcal{L}({\vect{2}\atop\Sigma};\neg\vect{w}(x_1,\square))=\left({0\atop\Sigma}\right)^*\left({1\atop\Sigma}\right) \left({0\atop\Sigma}\right)^*\left({0\atop\square}\right)^+$ $\mathcal{L}(\Sigma;\exists x_1\ \neg\vect{w}(x_1,\square)) =\Sigma^+\square^+$ $\mathcal{L}(\forall x_1\,\vect{w}(x_1,\square))=\mathcal{L}(\Sigma;\neg\exists x_1\ \neg\vect{w}(x_1,\square)) =\Sigma^*\square^+-\Sigma^+\square^+=\{\varepsilon\}\square^+$

例２．$\forall x_1\exists x_2\ x_1{\lt}x_2\wedge\vect{w}(x_2,a)\equiv\neg\exists x_1\,\neg(\exists x_2\ x_1{\lt}x_2\wedge\vect{w}(x_2,a))$に対し、 $\mathcal{L}\left({{\vect{2}\atop\vect{2}}\atop\Sigma};x_1{\lt}x_2 \wedge \vect{w}(x_2,a)\right)= \left({{0\atop 0}\atop\Sigma}\right)^*{{1\atop 0}\atop\Sigma}\left({{0\atop 0}\atop\Sigma}\right)^*{{0\atop 1}\atop a}\left({{0\atop 0}\atop\Sigma}\right)^*\left({{0\atop 0}\atop\square}\right)^+$ $\mathcal{L}({\vect{2}\atop\Sigma};\exists x_2\ x_1{\lt}x_2 \wedge \vect{w}(x_2,a))= \left({0\atop\Sigma}\right)^*{1\atop\Sigma}\left({0\atop\Sigma}\right)^*{0\atop a}\left({0\atop \Sigma}\right)^*\left({0\atop\square}\right)^+$ $\mathcal{L}({\vect{2}\atop\Sigma};\neg(\exists x_2\ x_1{\lt}x_2 \wedge \vect{w}(x_2,a))) =\left(\varepsilon \cup\left({0\atop\Sigma}\right)^*{1\atop\Sigma}\left({0\atop \Sigma{-}a}\right)^*\right)\left({0\atop\square}\right)^+$ $\mathcal{L}(\Sigma;\exists x_1\ \neg(\exists x_2\ x_1{\lt}x_2 \wedge \vect{w}(x_2,a))) =(\varepsilon \cup\Sigma^+(\Sigma{-}a)^*)\square^+=\Sigma^*\square^+$ $\mathcal{L}(\forall x_1\exists x_2\ x_1{\lt}x_2\wedge\vect{w}(x_2,a))=\mathcal{L}(\Sigma;\neg\exists x_1\ \neg(\exists x_2\ x_1{\lt}x_2 \wedge \vect{w}(x_2,a))) =\emptyset$

例３．図で与えられるDFA$M~(Q,\Sigma,\delta,p.\{p\})$が認識する言語は論理式

$\exists\vect{u}\forall x\psi(x,\vect{u},\vect{v}),\\ \psi(x,\vect{u},\vect{v}):\equiv (x{=}0{\to}\vect{u}(x,p))\wedge \left(\;\vect{u}(x,p){\wedge}\vect{v}(x,\square){\wedge}\vect{u}(x{+}1,\square)\\ %\wedge (\vect{u}(x,\square){\to}\vect{v}(x,\square)) \vee \vect{u}(x,p){\wedge}\vect{v}(x,a){\wedge}\vect{u}(x{+}1,p) \vee \vect{u}(x,p){\wedge}\vect{v}(x,b){\wedge}\vect{u}(x{+}1,q)\\ \vee \vect{u}(x,q){\wedge}\vect{v}(x,a){\wedge}\vect{u}(x{+}1,q) \vee \vect{u}(x,q){\wedge}\vect{v}(x,b){\wedge}\vect{u}(x{+}1,p)\;\right)$ で表せ、$\mathcal{L}\left({Q\atop\Sigma};\forall x\,\psi(x,\vect{u},\vect{v})\right) =\left({p\atop a}\cup {p\atop b}\left({q\atop a}\right)^*{q\atop b}\right)^* {p\atop \square}\left({\square\atop\square}\right)^+$より、
$\mathcal{L}\left(\Sigma;\exists\vect{u}\forall x\,\psi(x,\vect{u},\vect{v})\right) {=}\left({a}{\cup}{b}{a}^*{b}\right)^*\square\square^+,\ \mathcal{L}(\exists\vect{u}\forall x\psi(x,\vect{u},\vect{v})){=}\left({a}{\cup} {b}{a}^*{b}\right)^*{=}\mathcal{L}(M)$。
　実際、$\forall x$ に関する煩雑な議論を簡素化して解釈世界を考えれば $E_{Q\Sigma}:=\left({Q\atop\Sigma}\right)^*\left(\left({Q\atop\square}\right)^* {\cup} \left({\square\atop\Sigma}\right)^*\right)\left({\square\atop\square}\right)^+{=}\mathcal{U}({Q\atop\Sigma}),\ E_Q:=\left({Q\atop\square}\right)^*\left({\square\atop\square}\right)^+$として、
$\pi_{23}(\mathcal{L}\left({\vect{2}\atop{Q\atop\Sigma}};\psi(x,\vect{u},\vect{v})\right)) =\left(\color{red}{p\atop \Sigma}E_{Q\Sigma}{\cup}\color{red}{p\atop \square}E_Q\right) \cap \left(\;\left({Q\atop \Sigma}\right)^*\left({Q\atop\square}\right)^* \color{red}{{p\atop\square}{\square\atop\square}}\left({\square\atop\square}\right)^*\\ 　　\cup\left({Q\atop \Sigma}\right)^*\left(\left(\color{red}{{p\atop a}{p\atop\Sigma}}{\cup}\color{red}{{p\atop b}{q\atop\Sigma}}{\cup}\color{red}{{q\atop a}{q\atop\Sigma}}{\cup}\color{red}{{q\atop b}{p\atop\Sigma}}\right)E_{Q\Sigma} \cup\left(\color{red}{{p\atop a}{p\atop\square}}{\cup}\color{red}{{p\atop b}{q\atop\square}}{\cup}\color{red}{{q\atop a}{q\atop\square}}{\cup}\color{red}{{q\atop b}{p\atop\square}}\right) E_{Q}\right)\;\right)$
$\forall x\,\psi(x,\vect{u},\vect{v}){\equiv}\neg\exists x\,\neg\psi(x,\vect{u},\vect{v})$は、赤字の位置に赤字と異なる文字列(パターン)が存在しないという意味だから
$\mathcal{L}\left({Q\atop\Sigma};\forall x\,\psi(x,\vect{u},\vect{v})\right) =\left({p\atop \Sigma}E_{Q\Sigma}{\cup}{p\atop \square}E_Q\right)\\ 　　- \left({Q\atop \Sigma}\right)^*\left(\left({Q\atop\square}\right)^*{Q\atop\square}{Q\atop\square}{\cup}\left({Q\atop\square}{-}{p\atop\square}\right) {\cup}\left({\square\atop\Sigma}\right)^*\right)\left({\square\atop\square}\right)^+\\ 　　-\left({Q\atop \Sigma}\right)^*\left(\left({Q\atop\Sigma}{Q\atop\Sigma}{-}{p\atop a}{p\atop\Sigma}{-}{p\atop b}{q\atop\Sigma}{-}{q\atop a}{q\atop\Sigma}{-}{q\atop b}{p\atop\Sigma}\right)E_{Q\Sigma} \cup \left({Q\atop\Sigma}{Q\atop\square}{-}{p\atop a}{p\atop\square}{-}{p\atop b}{q\atop\square}{-}{q\atop a}{q\atop\square}{-}{q\atop b}{p\atop\square}\right)E_{Q}\right)\\ =\left({p\atop a}\cup {p\atop b}\left({q\atop a}\right)^*{q\atop b}\right)^* {p\atop \square}\left({\square\atop\square}\right)^+$

出力付き有限オートマトン

　有限オートマトンの遷移に出力を付けた機械をミーリ機械と呼ぶ。形式的にはミーリ機械$M=(Q,\Sigma,\Gamma,\delta,q_0)$の時点表示は (状態$\cdot$未読文字列$;$出力文字列)${}\in Q\Sigma^*;\Gamma^*$で、$(q,a;\alpha,p)\in \delta\subseteq Q{\times}\Sigma^?{\times}\Gamma^*{\times}Q \rlarrow (qa\vect{w};\beta)\vdash (p\vect{w};\beta\alpha)$が成立ち、$M$は入出力関係$\{(\vect{w},\alpha)\mid q_0\vect{w};\VDASH{}{*}q;\alpha\}$を計算する。即ち$(q,a;\alpha,p)$は状態$p$と入力$a$に対し$\alpha$を出力し$q$へ遷移することを表し$\circled{p}\labelarrow{a;\alpha}\circled{q}$のように図示する。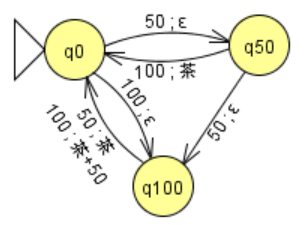

例．右図は、50円玉と100円玉のみを受け付ける150円のお茶(1種類)の簡単な自動販売機を表すミーリ機械である。状態名の$q$に続く数値はそれまでに投入された金額を表し、出力はお茶とおつりである。
　この例が示すように、ミーリ機械は、ある時点の出力が(初期状態から)それまでの入力列によって決まる機械で、入力列に関する情報があらかじめ定まった数の状態で表現(記憶)されるものをいう。即ち、ミーリ機械は一般的に、メモリが有限の(外部記憶を持たない)機械の数学的モデルと見做すことができる。

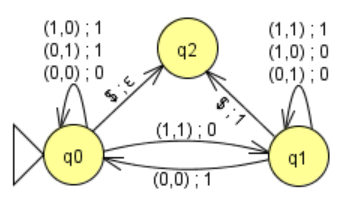
例．右図は2進和を(1桁目から)順に計算するミーリ機械で、$q_0\ (q_1)$ は繰上りが$0\ (1)$ の状態を表し、$a_n\cdots a_2a_1+b_n\cdots b_2b_1=c_{n+1}c_n\cdots c_2c_1$のとき、入力$(a_1,b_1)(a_2,b_2)\cdots(a_n,b_n)\$$に対し$c_1c_2\cdots c_nc_{n+1}$を出力する。
　一方、出力が遷移でなく状態に付随する有限オートマトンをムーア機械といい、ミーリ機械と計算能力が等しいことが知られているが、詳細は省略する。