論理関数とその応用第一部


論理関数とその応用
第一部















この教科書はBookletを利用して作成している。
本書の見方
ページをめくる
左(右)ページの左(右)端クリックまたはドラッグする
左(右)矢印キーを押す
１ページ分の移動
左右上端にある[Next]、[Previous]タブをクリックする
章の頭に移動
右上の【章の移動】タブをクリックし、現れた章を選ぶ
ページのジャンプ
右上のページ番号表示タブをクリックし、現れたページを選ぶ
画像の拡大およびリンク先への移動
画像やリンク先をクリックすれば、別ウィンドウ(タブ)で表示される

目　次

第一部
　０章　学習の指針
　１章　論理と集合
集合の記法
命題論理とその記法
１変数述語と集合
基本等式
基本不等式
双対原理
公式の証明
　２章　論理回路
AND、OR、NOT素子
論理式（回路）の設計
加算器
集積回路の原理

第二部
　３章　論理関数
論理関数の定義
排他的論理和に関する公式
標準形
標準形の求め方
論理式の簡単化
　４章　順序回路
順序回路とは
順序回路の能力
状態の符号化
　５章　論理関数族の理論
閉関数族
完全性


第０章　学習の指針

０．１節　学習の指針

　「論理関数と応用」では、$\{0,1\}$上の関数について、その基礎を、計算機科学への応用を含めて学んでゆく。コンピュータ回路への応用についても触れるが、回路の物理的な側面には立ち入らない。
　第一部の第１章では、本講義の基礎となる論理と集合の基本的な記法や公式・技法を学ぶ。第２章では、論理回路の基礎を紹介し、論理式と論理回路の関係を示す。
　第二部の第３章では、論理式を論理関数として捉え直し、標準形やその簡単化の問題を扱う。第４章では、論理回路に記憶素子を付け加えた順序回路について、取り扱う。さらに、第５章では、順序回路の数学的モデルである有限オートマトンの理論を、第６章では論理関数の完全性の問題と関連して論理関数族の理論を紹介する。

　授業では、折に触れて課題を提示するので、積極的に挑戦してもらいたい。


参考書
野﨑昭弘著「スイッチング理論」共立出版（１９７２）
南谷崇著「論理回路の基礎」サイエンス社（２００９）

第１章　準備：論理と集合

【この章のポイント】

この章では、集合と論理の基本的な記法および事項を学習する。

【この章の目標】学習後、以下のことが身についたかチェックしよう。

  1. 集合の基本的な記法を理解できる
  2. 論理の基本的な記法を理解できる
  3. 集合と論理の関係を理解している
  4. 双対原理を理解している
  5. ベン図が書ける
  6. 真理値表が使える


【この章の構成】

  1. 集合の記法
  2. 命題論理とその記法
  3. １変数述語と集合
  4. 基本等式
  5. 基本不等式
  6. 双対原理
  7. 公式の証明

１．１節　集合の記法

　集合はもの(要素)の集まりで、その表し方には、$\{2,3,5,7\}$ のように、$\{,\ \}$ の間に要素を列挙する外延的記法と、要素が集合に属する条件を記述する内包的記法がある。
  • 外延的記法では、列挙する要素の重複や並び順は無視されるので、$\{2,3,5,7\}=\{2,3,7,3,5\}$
  • 内包的記法では、例えば $\{x\;|\;x\ は10以下の素数\}$ の $x$ のように、要素を表す変数を利用する
集合 $A$ の要素の個数を $|A|$ で表す。例えば $|\{2,3,5,7\}|=4$ である。

以下、集合で使われる主な関係や演算を表す記号をまとめておこう。
$a{\color{blue}\in}A$要素 $a$ が集合 $A$ に属す（の要素である）
$A{\color{blue}\subseteq}B,\ B{\color{blue}\supseteq}A$集合 $A$ が集合 $B$ に含まれる
$A{\color{blue}=}B$$A$ と $B$ が等しい
$A{\color{blue}\subset}B,\ B{\color{blue}\supset}A$$A$ が $B$ に真に含まれる（含まれていてかつ等しくない）
$A{\color{blue}\cup}B:=\{x\;|\;x\in A\ または\ x\in B\}$$A$ と $B$ の和集合
$A{\color{blue}\cap}B:=\{x\;|\;x\in A\ かつ\ x\in B\}$$A$ と $B$ の積集合
$A{\color{blue}-}B:=\{x\;|\;x\in A\ かつ\ x\not\in B\}$$A$ から $B$ を引いた差集合
$A^{\color{blue}C}:=U-A$$A$ の補集合。$U$ は議論している世界の要素全体からなる全体集合
注．$:=$は「左辺を右辺で定義する」という意味

問．以下の問に答えよ
  1. 領域 $A\cap B$ を構成する領域の番号を示せ
  2. 領域 $A\cup B$ を構成する領域を番号で示せ
  3. 領域 $A-B$ を構成する領域の番号を示せ
  4. 領域 $A^C$ を構成する領域を番号で示せ

１．２節　命題論理とその記法

　真偽が定まっている文を命題という。命題から新たな命題を作り出す演算（操作）として、連言 $\wedge$（かつ）、選言 $\vee$（または）、否定 $\neg$（でない）などが知られており、命題 $P,\ Q$ に対し、命題$ P\wedge Q$ は「$P$ かつ $Q$」を、命題 $P\vee Q$ は「$P$ または $Q$」を、命題 $\neg P$ は「$P$ でない」を意味する命題である。したがって、その真偽を表にすると、次のようになる。

$P$$Q$連言 $P\wedge Q$選言 $P\vee Q$
偽偽偽偽
偽真偽真
真偽偽真
真真真真
$P$否定 $\neg P$
偽真
真偽



命題(変数)から $\wedge,\ \vee,\ \neg$ を使って構成される式を論理式と呼ぶ。

注．$偽=P\wedge \neg P,\ 真=P\vee \neg P$（次ページの表の補元則）だから、論理式には $真,偽$ を含めてもよい。また逆に、論理式中の $真,偽$ は、次ページの表のゼロ元・単位元の法則、補元則等を用いて消去できる。

１．３節　１変数述語と集合

集合の内包的記法では、$A=\{x\;|\;\mathcal{A}(x)\}（=\{x\;|\;\mathcal{A}(x) が成立つ\}）$という記法が用いられた。ここで、$\mathcal{A}(x)$ を $x$ に関する条件を表す1変数述語（命題関数）といい、$x$ に具体的に「もの」(全体集合の要素）を代入すると真偽が定まり命題になる。このとき
$x\in A \iff \mathcal{A}(x)（=真）$
が成り立つ。この観点からは、集合と1変数述語は同じものと見做せる。$A=\{x\;|\;\mathcal{A}(x)\},\ B=\{x\;|\;\mathcal{B}(x)\}$ のとき次が成り立つ。
$x\in A\cap B \iff \mathcal{A}(x)\wedge \mathcal{B}(x)（=真）\\ x\in A\cup B \iff \mathcal{A}(x)\vee \mathcal{B}(x)（=真）\\ x\in A^C \iff \neg \mathcal{A}(x)（=真）$
問．$A=\{x\;|\;\mathcal{A}(x)\},\ B=\{x\;|\;\mathcal{B}(x)\},\ C=\{x\;|\;\mathcal{C}(x)\}$ とする。以下の問に答えよ

領域番号$A\ B\ C$集合演算式論理式
$0$$0\ 0\ 0$$A^C\cap B^C\cap C^C$$\neg \mathcal{A}(x)\wedge \neg \mathcal{B}(x)\wedge \neg \mathcal{C}(x)$
$1$
$2$
$3$$0\ 1\ 1$$A^C\cap B\cap C$$\neg \mathcal{A}(x)\wedge \mathcal{B}(x)\wedge \mathcal{C}(x)$
$4$
$5$
$6$
$7$

１．左上図は、集合 $A,\ B,\ C$ のベン図である。$0$ から $7$ までの番号を付けた集合を表す集合演算式(や論理式)を表す右上の表の空欄を埋めよ。ここで、$A$ の欄には、対応する集合が $A$ に含まれない場合は $0$ を $A$ に含まれる場合は $1$ を入れ、$B$、$C$ の欄にも同様に記入せよ。

２．集合 $A,\ B,\ C$ で区分けされる集合はすべて、$0$ から $7$ までの番号づけられた集合の和集合で表されるから、$A,\ B,\ C$ から $\cap,\ \cup,\ ^C$（$\mathcal{A}(x),\ \mathcal{B}(x),\ \mathcal{C}(x)$ から $\wedge,\ \vee,\ \neg$）の組み合わせで得られる集合演算式（論理式）で表される。
１)$1,\ 3,\ 5$ の和集合を表す集合演算式（および論理式）を求めよ。
２)$1,\ 3,\ 5$ の和集合を表す集合演算式（および論理式）をできるだけ簡単な形で表せ。

３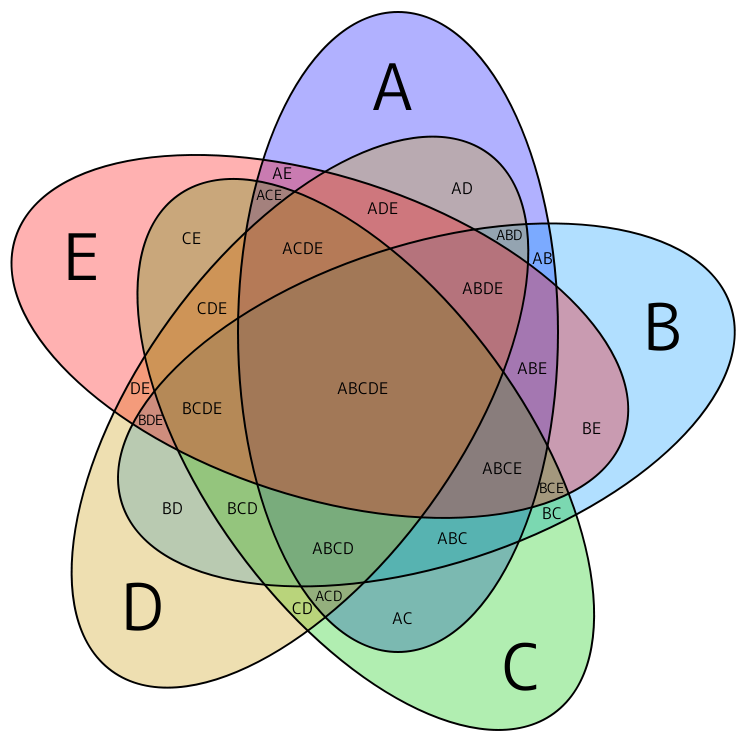． 画像 右図は、Branko Grunbaumが考案した楕円を用いた5集合ベン図である。全体集合がいくつの集合(領域)に分割されているか。(Wikipedia)

１．４節　基本等式

命題論理（集合）で成り立つ基本的な等式をあげておこう。

名称命題論理集合　$U$は全体集合
ベキ等則$P\wedge P=P\vee P=P$$A\cap A=A\cup A=A$
結合則$(P\wedge Q)\wedge R=P\wedge(Q\wedge R)$
$(P\vee Q)\vee R=P\vee(Q\vee R)$		 $(A\cap B)\cap C=A\cap(B\cap C)$
$(A\cup B)\cup C=A\cup(B\cup C)$
交換則$P\wedge Q=Q\wedge P,\ P\vee Q=Q\vee P$$A\cap B=B\cap A,\ A\cup B=B\cup A$
吸収則$(P\wedge Q)\vee P=(P\vee Q)\wedge P=P$ $(A\cap B)\cup A=(A\cup B)\cap A=A$
分配則$(P\wedge Q)\vee R=(P\vee R)\wedge(Q\vee R)$
$(P\vee Q)\wedge R=(P\wedge R)\vee(Q\wedge R)$		 $(A\cap B)\cup C=(A\cup B)\cap(B\cup C)$
$(A\cup B)\cap C=(A\cap C)\cup(B\cap C)$
二重否定則$\neg(\neg P)=P$$(A^C)^C=A$
補元則$P\wedge \neg P=偽,\ P\vee \neg P=真$$A\cap A^C=\emptyset,\ A\cup A^C=U$
ゼロ元$P\wedge 偽=偽,\ P\vee 真=真$$A\cap \emptyset=\emptyset,\ A\cup U=U$
単位元$P\wedge 真=P,\ P\vee 偽=P$$A\cap U=A,\ A\cup \emptyset=A$
ド・モルガン
の定理		$\neg(P\wedge Q)=\neg P \vee \neg Q$
$\neg(P\vee Q)=\neg P \wedge \neg Q$		 $(A\cap B)^C=A^C\cup B^C$
$(A\cup B)^C=A^C\cap B^C$

１．５節　基本不等式

命題論理で、$偽<真$ とおくと、$P\wedge Q=\min(P,Q),\ P\vee Q=\max(P,Q)$ が成立つ。

名称命題論理集合
$偽\leqq P\leqq 真$$\emptyset\subseteq A\subseteq U$
$P\wedge Q \leqq P\leqq P\vee Q$ $A\cap B\subseteq A\subseteq A\cup B$
$P\leqq Q \Leftrightarrow \neg Q\leqq \neg P$$A\subseteq B \Leftrightarrow B^C \subseteq A^C$
$P\leqq Q \Leftrightarrow P\wedge Q=P\Leftrightarrow P\vee Q=Q$ $A\subseteq B\Leftrightarrow A\cap B=A\Leftrightarrow A\cup B=B$
$P\leqq Q \Leftrightarrow \neg P\vee Q=真\Leftrightarrow P\wedge \neg Q=偽$ $A\subseteq B\Leftrightarrow A^C\cup B=U\Leftrightarrow A\cap B^C=\emptyset$
$P\leqq R,Q\leqq S\Rightarrow$
$P\wedge Q\leqq R\wedge S,P\vee Q\leqq R\vee S$		 $A\subseteq C,B\subseteq D\Rightarrow$
$A\cap B\subseteq C\cap D,A\cup B\subseteq C\cup D$
$P\not\leqq Q\Leftrightarrow P>Q\Leftrightarrow P=真,\ Q=偽$

ただし、不等式の表の最後の公式は、値が$真$、$偽$の２通りしかないことに基づいており、対応する集合の公式はない。

１．６節　双対原理

　真理値表において$真$と$偽$を交換すると、$\wedge$ の表は $\vee$ の表に、$\vee$ の表は $\wedge$ の表に、$\neg$ の表は $\neg$ 自身に、なる。このことから、命題論理の等式において $\wedge$ と $\vee$、$真$と$偽$を交換した等式もまた成り立つ。基本等式の表において、このことが成立していることを確認してみよう。
　論理式 $\alpha$ に対し、$\wedge$ と $\vee$、$真$と$偽$を交換してえられる式 $\alpha^*$ を $\alpha$ の双対式という。上で述べたことから $\alpha=\beta$ ならば $\alpha^*=\beta^*$ が成り立つ。さらに、$真$と$偽$を交換すれば、不等式の方向は逆になるから、$\alpha\leqq \beta$ ならば $\beta^*\leqq \alpha^*$ である(基本不等式の表で確認せよ)。これらを双対原理という。
　双対原理は、述語と集合の関係から、集合の等式や不等式についても成り立つ。

問．次の命題論理式・集合演算式の双対形を求めよ
  1. $(P\vee Q)\wedge R$
  2. $(A\cap B)\cup A=A$
  3. $P\leqq P\vee Q$

１．７節　公式の証明

論理式や集合演算の等式や不等式を証明を与えずに列挙したが、それらの証明には、次のような道具を利用すると便利である。以下、具体的に例を挙げて、説明しよう。

（１）真理値表による証明

命題論理式に関する証明には、真理値表という、式中の変数の真・偽に応じた論理式の真・偽の表が利用できる。

$P$$Q$$P\wedge Q$$\neg(P\wedge Q)$$\neg P$$\neg Q$$\neg P\vee \neg Q$
$0$偽偽偽真真真真
$1$偽真偽真真偽真
$2$真偽偽真偽真真
$3$真真真偽偽偽偽

ド・モルガンの定理 $\neg(P\wedge Q)=\neg P \vee \neg Q$
∵）右の真理値表より、$\neg(P\wedge Q)$ と $\neg P \vee \neg Q$ の列の値は一致するから、$\neg(P\wedge Q)=\neg P \vee \neg Q$ である。

$P$$Q$$R$$P\wedge Q$$(P\wedge Q)\vee R$$P \vee R$$Q \vee R$$(P \vee R)\wedge(Q\vee R)$
$0$偽偽偽偽偽偽偽偽
$1$偽偽真偽真真真真
$2$偽真偽偽偽偽真偽
$3$偽真真偽真真真真
$4$真偽偽偽偽真偽偽
$5$真偽真偽真真真真
$6$真真偽真真真真真
$7$真真真真真真真真

分配則 $(P\wedge Q)\vee R=$
$(P\vee R)\wedge(Q\vee R)$
∵）右の真理値表より、$(P\wedge Q)\vee R$ と $(P\vee R)\wedge(Q\vee R)$ の列は一致するから、 $(P\wedge Q)\vee R=$
$(P\vee R)\wedge(Q\vee R)$ である。
$P$$Q$$P\wedge Q$$P\wedge Q\leqq P$
$0$偽偽偽真
$1$偽真偽真
$2$真偽偽真
$3$真真真真

不等式に関する公式 $P\wedge Q\leqq P$
∵）右の真理値表でどの行においても $(P\wedge Qの値)\leqq(Pの値)$ が成立つ。

$P$$Q$$P\leqq Q$$P\wedge Q$$P\wedge Q=P$$P\vee Q$$P\vee Q=Q$
$0$偽偽真偽真偽真
$1$偽真真偽真真真
$2$真偽偽偽偽真偽
$3$真真真真真真真

$P\leqq Q \Leftrightarrow P\wedge Q=P\Leftrightarrow P\vee Q=Q$
∵）右の真理値表で $P\leqq Q,\ P\wedge Q=P,\ P\vee Q=Q$ が成り立つ行は、どれも $0,\ 1,\ 3$ 行で、これらの列の値は一致している。

問．以下の式を、真理値表を作成して証明せよ。
  1. $(P\wedge Q)\vee P=(P\vee Q)\wedge P=P$
  2. $P\leqq Q \Leftrightarrow \neg Q\leqq \neg P$
  3. $P\not\leqq Q\Leftrightarrow P>Q\Leftrightarrow P=真,Q=偽$

（２）ベン図による証明

　集合に関する公式の証明には以下のようなベン図を使うと便利である。


ド・モルガンの定理 $(A\cap B)^C=A^C \cup B^C$
∵）右のベン図で、$A\cap B$ が表す領域は $3$ だから、$(A\cap B)^C$ は $0,\ 1,\ 2$ を合わせた領域を表す。一方、$A^C$ は $0,\ 1$ を合わせた領域を表し、$B^C$ は $0,\ 2\ $を合わせた領域を表すから、$A^C \cup B^C$ は $0,\ 1,\ 2$ を合わせた領域を表し、$(A\cap B)^C$ が表す領域と一致する。

分配則 $(A\cap B)\cup C=(A\cup C)\cap (B\cup C)$
∵）右のベン図で、上と同様の議論を行うと、$(A\cap B)\cup C$ と $(A\cup C)\cap (B\cup C)$ が表す領域は、ともに $1,\ 3,\ 5,\ 7,\ 6$ を合わせた領域である。

不等式に関する公式 $A\cap B\subseteq A$
∵）$A\cap B$ の領域は $3$ だから、あきらかに（領域 $2,\ 3$ から構成される）$A$ に含まれる。

$A\subseteq B \Leftrightarrow A\cap B=A\Leftrightarrow A\cup B=B$
∵）$A\subseteq B,\ A\cap B=A,\ A\cup B=B$ のどれも、右上のベン図で $2$ の領域がないことを意味し、ベン図は右図のようになる。よってこれらの条件は同値である。

問．以下の式を、ベン図を用いて証明せよ。
  1. $(A\cap B)\cup A=(A\cup B)\cap A=A$
  2. $A\subseteq B \Leftrightarrow B^C\subseteq A^C$
  3. $A\subseteq B\Leftrightarrow A^C\cup B=U\Leftrightarrow A\cap B^C=\emptyset$
　１．１．３に述べた観点からすれば、真理値表による論理式の証明とベン図による集合の式の証明は、実質的に同等である。
　実際、$A=\{x\;|\;\mathcal{A}(x)\},\ B=\{x\;|\;\mathcal{B}(x)\}$ なら、例えば
$(A\cap B)^C=\{x\;|\;\neg(\mathcal{A}(x)\wedge \mathcal{B}(x))\},\ A^C \cup B^C=\{x\;|\;\neg \mathcal{A}(x)\vee \neg \mathcal{B}(x)\}$ であるから、$(A\cap B)^C=A^C \cup B^C \iff すべての\;x\;に対して\ \neg(\mathcal{A}(x)\wedge \mathcal{B}(x))=\neg \mathcal{A}(x)\vee \neg \mathcal{B}(x)\\ \iff \neg(P \wedge Q)=\neg P \vee \neg Q$
である。また、例えば
$A\cap B\subseteq B \iff すべての\;x\;に対して\mathcal{A}(x)\wedge\mathcal{B}(x)\leqq \mathcal{B}(x)\iff P\wedge Q \leqq Q$

である。

（３）推論（演繹）による証明

　集合の公式の多くは、（２）の最後に議論したことから、命題論理の公式に帰着され、それは論理的推論（演繹）によって証明できる。以下論理値に順序 $偽\lt 真$ を仮定すると $P \vee Q=\max(P,Q),\ P\wedge Q=\min(P,Q)$ となることも利用し、論理公式を証明してみよう。
　ベキ等則 $P\wedge P=\min(P,P)=P,\ P\vee P=\max(P,P)=P$、
　結合則 $(P\wedge Q)\wedge R=\min(P,Q,R)=P\wedge(Q\wedge R),\\ (P\vee Q)\vee R=\max(P,Q,R)=P\vee(Q\vee R)$、
　交換則 $P\wedge Q=\min(P,Q)=Q\wedge P,\ P\vee Q=\max(P,Q)=Q\vee P$、
　吸収則 $P\wedge Q\leqq P\leqq P\vee Q$ より、$(P\wedge Q)\vee P=(P\vee Q)\wedge P=P$
がいえる。また、$偽\leqq P\leqq 真$ であることに注意すれば、ゼロ元と単位元の法則が導かれる。
　分配則の証明：$R=真$ならば、$(P\wedge Q)\vee R=真=(P\vee R)\wedge(Q\vee R)$。$R=偽$ならば、$(P\wedge Q)\vee R=P\wedge Q=(P\vee R)\wedge(Q\vee R)$。よって、$(P\wedge Q)\vee R=(P\vee R)\wedge(Q\vee R)$。

問．以下の式を演繹的に証明せよ。
  1. 集合の分配法則 $(A\cap B)\cup C=(A\cup C)\cap (B\cup C)$
  2. $A\subseteq C,\ B\subseteq D\Longrightarrow A\cap B\subseteq C\cap D$

第２章　論理回路

【この章のポイント】

　コンピュータが $0,\ 1$ で動いている。CPU（頭脳部）での演算は、加算でも他の演算でも、結局のところ与えられた複数の32（あるいは64）桁の $0,\ 1$ 入力列から32（あるいは64）桁の $0,\ 1$ 出力列を求めることに他ならない。
　本章で扱う論理回路や第４章で扱う順序回路は、コンピュータの頭脳部を構成する電子回路で、$0, 1$ の入力列に対し $0, 1$ 列を出力する。この章では、論理回路の設計の基本を学び、論理回路が AND, OR, NOT という3種類の素子からすべて構成できることを、回路シミュレータ―も使ってみてゆこう。
　では、論理回路は、これら3種類の素子を多量にかつ複雑に配置しつないでいるのだろうか。実はこれらの素子は(ひいては論理回路も)、原理的にはただ1種類の素子から組み立てられる。これを歴史的には、リレー、真空管、トランジスタを使って、実現されてきた。

【この章の目標】 学習後、以下のことが身についたかチェックしよう。

  1. AND、OR、NOT素子の働きを理解する
  2. 簡単な論理式（回路）の設計ができる
  3. 加算器の仕組みを理解する
  4. 集積回路の原理を理解する
  5. 回路シミュレータで簡単な回路を実現できる

【この章の構成】

  1. AND、OR、NOT素子
  2. 論理式（回路）の設計
  3. 加算器
  4. 集積回路の原理

２．１節　AND、OR、NOT 素子

　真を$1$、偽を$0$で表すと、前節で議論した論理演算は、左下の表になるが、AND($\wedge$), OR($\vee$), NOT($\neg$)の論理素子は、$0,\ 1$ の入力に対し、左下の出力表（真理値表）を持つ。
　このことを、右下の論理回路シミュレータで試してみよう。シミュレータでは、電源(DC)につながった入力ボタン($x$、$y$)をクリックすると、そのON($1$)/OFF($0$)に応じて回路の出力LEDが点($1$)滅($0$)する。
　（回路シミュレータは Kazuhiko Arase 氏による SimcirJS を利用している。参考ページ）

$x$$\neg x$
$0$$1$
$1$$0$
$x\ y$$x\wedge y$$x\vee y$
$0\ 0$$0$$0$
$0\ 1$$0$$1$
$1\ 0$$0$$1$
$1\ 1$$1$$1$
{"width":400, "height":400, "showToolbox":true, "toolbox":[ {"type":"NOT"},{"type":"AND"},{"type":"OR"}, {"type":"DC"},{"type":"LED"},{"type":"Toggle","label":"x"},{"type":"Toggle","label":"y"} ], "devices":[ {"type":"DC","id":"dev0","x":8,"y":16,"label":"DC"}, {"type":"LED","id":"dev1","x":160,"y":16,"label":"LED"}, {"type":"Toggle","label":"x","id":"dev2","x":56,"y":16,"state":{"on":false}}, {"type":"DC","id":"dev3","x":8,"y":80,"label":"DC"}, {"type":"Toggle","label":"x","id":"dev4","x":56,"y":80,"state":{"on":false}}, {"type":"LED","id":"dev5","x":160,"y":80,"label":"LED"}, {"type":"NOT","id":"dev6","x":112,"y":80,"label":"NOT"}, {"type":"Toggle","label":"x","id":"dev7","x":56,"y":136,"state":{"on":false}}, {"type":"Toggle","label":"y","id":"dev8","x":56,"y":192,"state":{"on":false}}, {"type":"AND","id":"dev9","x":120,"y":160,"label":"AND"}, {"type":"LED","id":"dev10","x":168,"y":160,"label":"LED"}, {"type":"DC","id":"dev11","x":8,"y":160,"label":"DC"} ], "connectors":[ {"from":"dev1.in0","to":"dev2.out0"}, {"from":"dev2.in0","to":"dev0.out0"}, {"from":"dev4.in0","to":"dev3.out0"}, {"from":"dev5.in0","to":"dev6.out0"}, {"from":"dev6.in0","to":"dev4.out0"}, {"from":"dev7.in0","to":"dev11.out0"}, {"from":"dev8.in0","to":"dev11.out0"}, {"from":"dev9.in0","to":"dev7.out0"}, {"from":"dev9.in1","to":"dev8.out0"}, {"from":"dev10.in0","to":"dev9.out0"} ] }

２．２節．論理式(回路)の設計

　論理回路を実現する原理を見てゆこう。この章のポイントでも述べたように、論理回路の働きは、複数の桁の $0,\ 1$ 入力から、複数の桁の $0,\ 1$ 出力を計算することなので、$0,\ 1$ の入出力関係を定める真理値表で与えられる。
　与えられた真理値表を持つ関数 $F$ を計算する回路を作る手順を考えよう。最初に、入出力ともに1ビットで2変数の場合を考えるが、ビット数や変数が増えても同様である。

２変数の例

$x\ y$$F(x,y)$その行だけ$1$で他は$0$の
真理値を持つ論理式
$0\ 0$$0$$\neg x \wedge \neg y$
$0\ 1$$1$$\neg x \wedge y$
$1\ 0$$1$$x\wedge \neg y$
$1\ 1$$0$$x \wedge y$
$F(x,y)=(\neg x \wedge y)\vee(x\wedge \neg y)$
与えられた真理値表を持つ論理式は次の手順で求められる。
  1. 真理値表の各行に対し、その行でだけ $1$ で他はすべて $0$ の真理値表を持つ論理式を求める。そのために、$x=0$ を意味する(と真偽が一致する)論理式が $\neg x$ であり、$x=1$ を意味する論理式が $x$ であることに注目する。したがって、求める論理式を得るには、入力値が $0$ の変数には$\neg$（NOT）を付けた上で、すべての変数を$\wedge$（AND）で結べばよい。
  2. 与えられた真理値表を持つ論理式を得るには、その値が $1$ である行について、上で求めた論理式を $\vee$（OR）で結べばよい。

実習．論理式の真理値表
　右の欄に論理式を入力して 評価 ボタンを押すと真理値表が表示される。論理記号は &(∧), |(∨), !(￢) を用い、例えば $(\neg x \wedge y)\vee(x\wedge \neg y)$ は !x&y|x&!y と表せる。
　適当な論理式を入力して確かめてみよ。


{"width":330, "height":130, "showToolbox":false, "toolbox":[{"type":"NOT"},{"type":"AND"},{"type":"OR"},{"type":"DC"},{"type":"LED"},{"type":"Toggle"}], "devices":[ {"type":"DC","id":"dev0","x":16,"y":48,"label":"DC"}, {"type":"Toggle","id":"dev1","x":64,"y":16,"label":"x","state":{"on":false}}, {"type":"Toggle","id":"dev2","x":64,"y":72,"label":"y","state":{"on":false}}, {"type":"NOT","id":"dev3","x":128,"y":8,"label":"NOT"}, {"type":"AND","id":"dev4","x":184,"y":24,"label":"AND"}, {"type":"AND","id":"dev5","x":184,"y":72,"label":"AND"}, {"type":"OR","id":"dev6","x":240,"y":48,"label":"OR"}, {"type":"LED","id":"dev7","x":288,"y":48,"label":"F(x,y)"}, {"type":"NOT","id":"dev8","x":128,"y":80,"label":"NOT"} ], "connectors":[ {"from":"dev1.in0","to":"dev0.out0"}, {"from":"dev2.in0","to":"dev0.out0"}, {"from":"dev3.in0","to":"dev1.out0"}, {"from":"dev4.in0","to":"dev3.out0"}, {"from":"dev4.in1","to":"dev2.out0"}, {"from":"dev5.in0","to":"dev1.out0"}, {"from":"dev5.in1","to":"dev8.out0"}, {"from":"dev6.in0","to":"dev4.out0"}, {"from":"dev6.in1","to":"dev5.out0"}, {"from":"dev7.in0","to":"dev6.out0"}, {"from":"dev8.in0","to":"dev2.out0"} ] }
詳しい説明は省略するが、与えられた論理式から、論理回路を構成することは難しくない。例えば論理式 $F(x,y)=(\neg x\wedge y)\vee (x\wedge \neg y)$ を実現する論理回路は右図のようになる。このように、コンピュータの演算回路は AND(∧)、OR(∨)、NOT(￢) の素子があれば組み立てられることがわかる。
$A\ B$$A+B$ の
上の桁$C$		$A+B$ の
下の桁$S$		その行だけ1
の論理式
$0\ \ 0$$0$$0$$\neg A \wedge \neg B$
$0\ \ 1$$0$$1$$\neg A \wedge B$
$1\ \ 0$$0$$1$$A \wedge \neg B$
$1\ \ 1$$1$$0$$A \wedge B$
論理式$C=A\wedge B$$S=(\neg A \wedge B)\vee(A\wedge \neg B)$

２．３節．加算器

　1ビットの加算を行なう半加算器を考えよう。加算の結果は、桁上がりを考慮して2ビットになるので、上下の桁の回路をそれぞれ構成する。右の表からわかるように、下の桁 $S$ の回路は、上で作成した例に他ならず、上の桁 $C$ は、ANDそのものである。これをもとに回路図を描くと下図のようになる。
{"width":500, "height":200, "showToolbox":true, "toolbox":[{"type":"NOT"},{"type":"AND"},{"type":"OR"},{"type":"DC"},{"type":"LED"},{"type":"Toggle"}], "devices":[ {"type":"OR","id":"dev0","x":264,"y":88,"label":"OR"}, {"type":"LED","id":"dev1","x":320,"y":8,"label":"C"}, {"type":"DC","id":"dev2","x":16,"y":72,"label":"DC"}, {"type":"Toggle","id":"dev3","x":80,"y":56,"label":"A","state":{"on":false}}, {"type":"AND","id":"dev4","x":144,"y":8,"label":"AND"}, {"type":"AND","id":"dev5","x":208,"y":64,"label":"AND"}, {"type":"NOT","id":"dev6","x":160,"y":56,"label":"NOT"}, {"type":"NOT","id":"dev7","x":160,"y":120,"label":"NOT"}, {"type":"AND","id":"dev8","x":208,"y":112,"label":"AND"}, {"type":"LED","id":"dev9","x":320,"y":88,"label":"S"}, {"type":"Toggle","id":"dev10","x":80,"y":120,"label":"B","state":{"on":false}} ], "connectors":[ {"from":"dev0.in0","to":"dev5.out0"}, {"from":"dev0.in1","to":"dev8.out0"}, {"from":"dev1.in0","to":"dev4.out0"}, {"from":"dev3.in0","to":"dev2.out0"}, {"from":"dev4.in0","to":"dev3.out0"}, {"from":"dev4.in1","to":"dev10.out0"}, {"from":"dev5.in0","to":"dev6.out0"}, {"from":"dev5.in1","to":"dev10.out0"}, {"from":"dev6.in0","to":"dev3.out0"}, {"from":"dev7.in0","to":"dev10.out0"}, {"from":"dev8.in0","to":"dev3.out0"}, {"from":"dev8.in1","to":"dev7.out0"}, {"from":"dev9.in0","to":"dev0.out0"}, {"from":"dev10.in0","to":"dev2.out0"} ] }
問．全加算器(桁上がり分も含めた加算回路)を実現する論理式
$C_{in}\ A\ B$$C_{in}+A+B$
上の桁$C_{out}$		$C_{in}+A+B$
下の桁$S$		その行だけ1の論理式
$0\ \ 0\ \ 0$$0$$0$$\neg C_{in} \wedge \neg A \wedge \neg B$
$0\ \ 0\ \ 1$$0$$1$$\neg C_{in} \wedge \neg A \wedge B$
$0\ \ 1\ \ 0$$0$$1$$\neg C_{in} \wedge A \wedge \neg B$
$0\ \ 1\ \ 1$$1$$0$$\neg C_{in} \wedge A \wedge B$
$1\ \ 0\ \ 0$$0$$1$$C_{in} \wedge \neg A \wedge \neg B$
$1\ \ 0\ \ 1$$1$$0$$C_{in} \wedge \neg A \wedge B$
$1\ \ 1\ \ 0$$1$$0$$C_{in} \wedge A \wedge \neg B$
$1\ \ 1\ \ 1$$1$$1$$C_{in} \wedge A \wedge B$
$C_{out}=$
$S=$
　右表は桁上がり $C_{in}$ の項も含めた全加算器の真理値表である。上の桁$C_{out}$と下の桁$S$を表す論理式をそれぞれ求めよ。
問．加算回路の実現
　全加算器は、問で得られた論理式からも構成できるが、$C_{in}+A+B=C_{in}+(A+B)$ なので、半加算器(HalfAdder)2個(とOR素子)を使っても構成できる。また、全加算器を(桁数)個並べれば、加算回路が実現できる。下の論理回路シミュレータで、
  1. 全加算器(Full Adder)を実現せよ
  2. 全加算器を使った４ビット加算器 $A_3A_2A_1A_0+B_3B_2B_1B_0=(C_{out})S_3S_2S_1S_0$ を実現せよ
{"width":600, "height":500, "showToolbox":true, "toolbox":[{"type":"HalfAdder"},{"type":"FullAdder"},{"type":"OR"},{"type":"4bitAdder"},{"type":"NOT"},{"type":"AND"},{"type":"DC"},{"type":"LED"},{"type":"Toggle"}], "devices":[ {"type":"DC","id":"dev0","x":0,"y":64,"label":"DC"}, {"type":"Toggle","id":"dev1","x":56,"y":0,"label":"Cin","state":{"on":false}}, {"type":"Toggle","id":"dev2","x":56,"y":64,"label":"A","state":{"on":false}}, {"type":"Toggle","id":"dev3","x":56,"y":120,"label":"B","state":{"on":false}}, {"type":"LED","id":"dev4","x":384,"y":24,"label":"S"}, {"type":"LED","id":"dev5","x":384,"y":88,"label":"Cout"}, {"type":"Toggle","id":"dev6","x":56,"y":192,"label":"A0","state":{"on":false}}, {"type":"Toggle","id":"dev7","x":56,"y":248,"label":"A1","state":{"on":false}}, {"type":"Toggle","id":"dev8","x":56,"y":304,"label":"A2","state":{"on":false}}, {"type":"Toggle","id":"dev9","x":56,"y":360,"label":"A3","state":{"on":false}}, {"type":"Toggle","id":"dev10","x":104,"y":224,"label":"B0","state":{"on":false}}, {"type":"Toggle","id":"dev11","x":104,"y":272,"label":"B1","state":{"on":false}}, {"type":"Toggle","id":"dev12","x":104,"y":336,"label":"B2","state":{"on":false}}, {"type":"Toggle","id":"dev13","x":104,"y":392,"label":"B3","state":{"on":false}}, {"type":"DC","id":"dev14","x":0,"y":280,"label":"DC"}, {"type":"LED","id":"dev15","x":320,"y":192,"label":"S0"}, {"type":"LED","id":"dev16","x":320,"y":248,"label":"S1"}, {"type":"LED","id":"dev17","x":320,"y":296,"label":"S2"}, {"type":"LED","id":"dev18","x":320,"y":352,"label":"S3"}, {"type":"LED","id":"dev19","x":320,"y":408,"label":"Cout"} ], "connectors":[ {"from":"dev1.in0","to":"dev0.out0"}, {"from":"dev2.in0","to":"dev0.out0"}, {"from":"dev3.in0","to":"dev0.out0"}, {"from":"dev6.in0","to":"dev14.out0"}, {"from":"dev7.in0","to":"dev14.out0"}, {"from":"dev8.in0","to":"dev14.out0"}, {"from":"dev9.in0","to":"dev14.out0"}, {"from":"dev10.in0","to":"dev14.out0"}, {"from":"dev11.in0","to":"dev14.out0"}, {"from":"dev12.in0","to":"dev14.out0"}, {"from":"dev13.in0","to":"dev14.out0"} ] }

２．４節．集積回路の原理

　すべての論理回路は $\wedge,\ \vee,\ \neg$ の3種類の素子から組み立てられる。CPUでは、これら3種類の素子を多量にかつ複雑に配置してつないでいるのだろうか。実はこれらの素子は、１種類のスイッチ素子から組み立てることができる。
　CPUでは、$0,\ 1$ は電流のON($1$)とOFF($0$)で表される。そこで、一方の電流の ON, OFF によって、もう一方の電流の ON, OFF を制御するスイッチがあれば、任意の論理回路が構成できることを見てゆこう。歴史的には、このようなスイッチにリレースイッチ、真空管、トランジスタ(半導体)などが使われてきた。

問７．６．AND、OR、NOT素子の設計：シミュレータを使って1～３を確かめ４に答えよ。
  1. スイッチ素子は、$X$ に電圧がかかる（$X=1$）と $Y$ と $Z$ が遮断され、$X=0$ のとき $Y$ と $Z$ がつながって電流が流れる
  2. $Y$ に電圧をかける（$Y＝1$）と、$X＝1$ のとき $Z=0$ で $X＝0$ のとき $Z=1$ だから、NOT の働きをする
  3. スイッチ素子を直列につないで右の $\neg$ につなぐと、$\neg(\neg X\wedge \neg Y)=X\vee Y$ なので OR ができる
  4. スイッチ素子を使って AND 素子を構成せよ
    ヒント：スイッチ素子の働きは $\neg X\wedge Y$ なので、$X$ 端子に $\neg X$ をつなげばよい。

{"width":620, "height":320, "showToolbox":true, "toolbox":[{"type":"DC"},{"type":"LED"},{"type":"Toggle"},{"type":"Switch"},{"type":"NOT"},{"type":"AND"},{"type":"OR"}], "devices":[ {"type":"DC","id":"dev0","x":0,"y":32,"label":"DC"}, {"type":"Toggle","id":"dev1","x":48,"y":0,"label":"X","state":{"on":false}}, {"type":"Switch","id":"dev2","x":112,"y":32,"label":"Switch"}, {"type":"Toggle","id":"dev3","x":48,"y":56,"label":"Y","state":{"on":false}}, {"type":"LED","id":"dev4","x":200,"y":32,"label":"LED"}, {"type":"DC","id":"dev5","x":256,"y":32,"label":"DC"}, {"type":"Switch","id":"dev6","x":368,"y":32,"label":"Switch"}, {"type":"Toggle","id":"dev7","x":312,"y":0,"label":"X","state":{"on":false}}, {"type":"LED","id":"dev8","x":456,"y":32,"label":"￢X"}, {"type":"Toggle","id":"dev9","x":48,"y":104,"label":"X","state":{"on":false}}, {"type":"Switch","id":"dev10","x":288,"y":176,"label":"Switch"}, {"type":"LED","id":"dev11","x":368,"y":176,"label":"X∨Y"}, {"type":"Toggle","id":"dev12","x":120,"y":104,"label":"Y","state":{"on":false}}, {"type":"Switch","id":"dev13","x":112,"y":152,"label":"Switch"}, {"type":"Switch","id":"dev14","x":200,"y":152,"label":"Switch"}, {"type":"DC","id":"dev15","x":0,"y":184,"label":"DC"}, {"type":"Toggle","id":"dev16","x":56,"y":216,"label":"X","state":{"on":false}}, {"type":"DC","id":"dev17","x":0,"y":248,"label":"DC"}, {"type":"LED","id":"dev18","x":304,"y":256,"label":"X∧Y"}, {"type":"Toggle","id":"dev19","x":56,"y":272,"label":"Y","state":{"on":false}} ], "connectors":[ {"from":"dev1.in0","to":"dev0.out0"}, {"from":"dev2.in0","to":"dev1.out0"}, {"from":"dev2.in1","to":"dev3.out0"}, {"from":"dev3.in0","to":"dev0.out0"}, {"from":"dev4.in0","to":"dev2.out0"}, {"from":"dev6.in0","to":"dev7.out0"}, {"from":"dev6.in1","to":"dev5.out0"}, {"from":"dev7.in0","to":"dev5.out0"}, {"from":"dev8.in0","to":"dev6.out0"}, {"from":"dev9.in0","to":"dev15.out0"}, {"from":"dev10.in0","to":"dev14.out0"}, {"from":"dev10.in1","to":"dev15.out0"}, {"from":"dev11.in0","to":"dev10.out0"}, {"from":"dev12.in0","to":"dev15.out0"}, {"from":"dev13.in0","to":"dev9.out0"}, {"from":"dev13.in1","to":"dev15.out0"}, {"from":"dev14.in0","to":"dev12.out0"}, {"from":"dev14.in1","to":"dev13.out0"}, {"from":"dev16.in0","to":"dev17.out0"}, {"from":"dev19.in0","to":"dev17.out0"} ] }
　このように、スイッチ素子のつなぎ方だけを変えることで、$\wedge,\ \vee,\ \neg$ 素子が実現でき、ひいては任意の演算回路が実現できる。したがってきわめて単純化して言えば、スイッチ素子を格子状に並べておいて、その間の配線を工夫すれば演算回路(CPU)が実現できる。半導体を使って一枚の基板上に、スイッチ素子を配線とともに直接作りこもうというのが集積回路のアイディアである。集積回路は格子間隔を細かくすればするほど小さくする（集積度を上げる）ことができる。

コラム．ティンカートイ コンピュータ
Tinkertoy Computer 　電子(電気)部品でなくとも、一方の ON/OFF で他方の ON/OFF が制御できればコンピュータを作れる。ティンカートイ(tinkertoy、木組みのおもちゃ)で、三目並べをするコンピュータをどうやって作るかに関する Dewdneyの記事 (SCIENTIFIC AMERICAN October 1989)を見よ。
SimcirJS のデモ：参考ページ）

{ "width":600, "height":600, "showToolbox":true, "toolbox":[ {"type":"In"}, {"type":"Out"}, {"type":"Joint"}, {"type":"DC"}, {"type":"LED"}, {"type":"PushOff"}, {"type":"PushOn"}, {"type":"Toggle"}, {"type":"BUF"}, {"type":"NOT"}, {"type":"AND"}, {"type":"NAND"}, {"type":"OR"}, {"type":"NOR"}, {"type":"EOR"}, {"type":"ENOR"}, {"type":"OSC"}, {"type":"7seg"}, {"type":"16seg"}, {"type":"4bit7seg"}, {"type":"RotaryEncoder"}, {"type":"BusIn"}, {"type":"BusOut"}, {"type":"RS-FF"}, {"type":"JK-FF"}, {"type":"T-FF"}, {"type":"D-FF"}, {"type":"8bitCounter"}, {"type":"HalfAdder"}, {"type":"FullAdder"}, {"type":"4bitAdder"}, {"type":"2to4BinaryDecoder"}, {"type":"3to8BinaryDecoder"}, {"type":"4to16BinaryDecoder"}, {"type":"Transmitter"}, {"type":"DSO"} ], "devices":[ ], "connectors":[ ] }