グラフとは
多くの問題が定式化(表現)可能
頂点（○や□で表す）を辺で結んだもの。
有向グラフ：有向辺（→）
無向グラフ：無向辺（―）
必要に応じて、頂点や辺にラベル
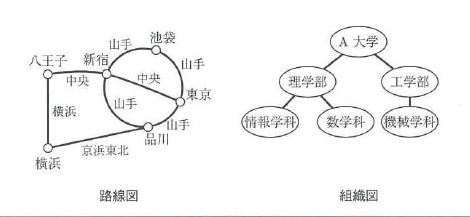
地下鉄路線図
放送大学組織図
ディズニーが描いた戦略図
グラフ理論の始まり
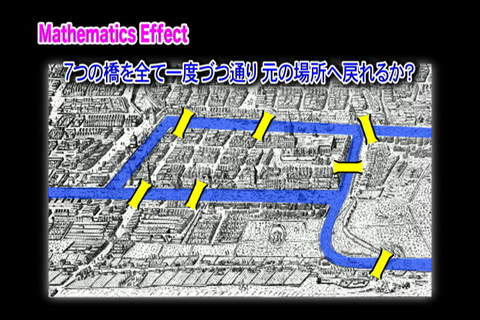
７つの橋を一度ずつ通る散歩道は？
オイラーは、グラフの一筆書きの問題に翻訳し、不可能であることを示した。
路：つながった辺の列
閉路：出発点に戻る路
オイラー路：すべての辺を1度ずつ通る路(一筆書き)
オイラー閉路：出発点に戻るオイラー路
パズル：ケーニヒスベルグの7つの橋を一度ずつ通る路はあるか。
同型なグラフ
同じグラフ：頂点の位置を適当に動かすと重なる（頂点の位置は無視）同型なグラフ：頂点の名前の付け替えで同じグラフと見なせる
パズル：図３.２ のG1とG2が同型であり、G3がそれらと同形でないことを示せ。
頂点探索アルゴリズム
定められた始点から到達可能な全頂点を一定の規則にしたがって訪問し処理する
頂点探索アルゴリズムの一般形
縁←{(始点,始点)}
縁が空でない間
辺$(u,v)$を縁から取り出す
$v$が未訪問なら
$v$を訪問し処理を行う
$v$の各辺$(v,w)$を縁に加える
縁からの辺取り出し方による分類
深さ優先探索：後に追加された辺を先に（LIFO）
幅優先探索 ：先に追加された辺を先に（FIFO）
最良優先探索：順位の高い辺を先に
深さ優先探索
始点から到達可能な全頂点を深さ優先で訪問し処理する縁をスタック(プッシュとポップ)で実現
プッシュ：列の後尾に追加
ポップ：列の後尾から取出し
深さ優先探索アルゴリズム
縁←[(始点,始点)]
縁が空でない間
辺$(u,v)$を縁からポップ
$v$が未訪問なら
$v$を訪問し処理を行う
$v$の各辺$(v,w)$を縁にプッシュ
幅優先探索
始点から到達可能な全頂点を幅優先（近いもの順）で訪問し処理する
縁をキュー（プッシュとシフト）で実現
プッシュ：列の後尾に追加
シフト：列の先頭から取出し
幅優先探索アルゴリズム
縁←[(始点,始点)]
縁が空でない間
辺$(u,v)$を縁からシフト
$v$が未訪問なら
$v$を訪問し処理を行う
$v$の各辺$(v,w)$を縁にプッシュ
最良（順位）優先探索
始点から到達可能な全頂点を優先順に訪問し処理する縁を順位キュー（プッシュと最良取出し）で実現
プッシュ：列に追加
最良取出し：列中の最良要素を取出し
最良優先探索アルゴリズム
縁←{(始点,始点,順位1)}
縁が空でない間
辺$(u,v,順位)$を縁から最良取出し
$v$が未訪問なら
$v$を訪問し処理を行う
$v$の各辺$(v,w,順位)$を縁にプッシュ
辺長優先探索：プラムのアルゴリズム
始点から到達可能な全頂点に至る重み最小の辺集合（最小全域木）を求めるプラムのアルゴリズム
縁←{(始点,始点,0)}；木←空
縁が空でない間
辺$(u,v,長さd)$を縁から$d$で最良取出し
$v$が未訪問なら
$v$を訪問済みにし辺$(u,v)$を木に追加
$v$の各辺$(v,w,長さ)$を縁にプッシュ
縁に対する操作（最良取出し、プッシュ）を効率的に実現するデータ構造
2分探索木
ヒープ
最短距離探索：ダイクストラのアルゴリズム
始点からの最短距離・経路を求めるダイクストラのアルゴリズム
縁←{(始点,始点,距離$0$)}；路←空
縁が空でない間
辺$(u,v,d)$を縁から距離$d$優先取出し
$v$が未訪問なら
$v$の距離を$d$(訪問済み)とし
$(u,v)$を路に追加
$v$の各辺$(v,w,l)$に対し
縁に$(v,w,d+l)$をプッシュ
縁に対する操作（最良取出し、プッシュ）を効率的に実現するデータ構造
2分探索木
ヒープ