フラクタルは自己相似図形と呼ばれ、図形の一部を拡大すると、再び同様の図形が現れるものをいいます。簡単な数式から美しいフラクタル画像が生成されます。今回は、p5.js という描画用言語を利用して、フラクタルの世界を探検します。
1.p5.js の利用
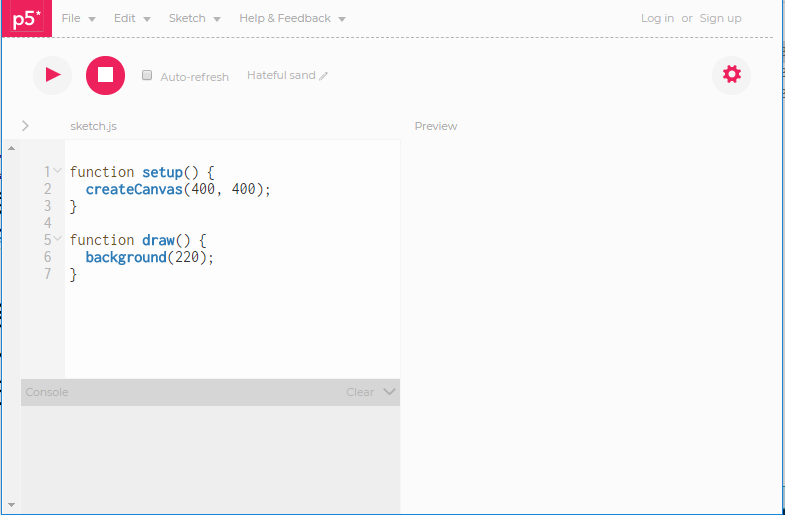
p5.js のウェブエディタ(https://alpha.editor.p5js.org/)にアクセスして利用します。(右図)
- 図左のエディタ欄にプログラムを入力し(▶)で実行すると、結果が右の Preview 欄に表示されます
- draw()関数はデフォルトで毎秒60回実行され、(■)で停止します
- プロジェクト名は、最初自動的につきますがクリックして変更できます
- ユーザ登録しなくても使えますが、プログラムの保存(読込)ができないので、以下の手順で登録を行います
利用登録【Sign Up】
- 利用に際し、次の情報をあらかじめ決めておきます
| User Name | ニックネームでかまいません |
| Email | Emailアドレス |
| Password | 忘れないものを |
- ウェブエディタ画面右上の Sign up をクリックすると、右の画面になります
- 1.の情報を入力(Confirm Password欄には確認のためパスワードを再入力)し Sign Up をクリックします
- 現れた画面の右上に Hello ユーザ名! と表示されればO.K.です
再利用【Log In】
- ウェブエディタ画面右上の Log In をクリックすると、右の画面になります
- 利用登録時に入力した情報、「Emailアドレス又は User Name」と「パスワード」を入力し Log In をクリックします
- 現れた画面の右上に Hello ユーザ名! と表示されればO.K.です
2.最初の p5.js プログラム
リサジュー図形はフラクタルではありませんが、p5.js の簡単な入門を兼ねて、作成します。
このプログラム
は $(\cos(nt),\,\sin(mt+d))$($0\leqq t\leqq 360^\circ$)で媒介変数表示されるリサジュー図形を描きます。プログラムを自分のp5.jsウェブエディタにコピーし、パラメータ $n,\,m,\,d$ の値を変えながら実行させてみましょう。
アニメーション版
はdraw()関数を利用して、描画過程をアニメーション表示します。
【補足】自分でプログラミングしてみようという方へ(p5.jsレファレンス)
- createCanvas($width,height$) は、左上が$\;(0,0)\;$で右下が$\;(width,height)\;$の描画面を生成します
- プログラムは、左上が$\;(-1,1)\;$で右下が$\;(1,-1)\;$の領域内の点($x,y$)を描画面の点$\;(width/2*(1+x),height/2*(1-y))\;$にマッピングしています
- point($x,y$) は、位置$\;(x,y)\;$に指定された色と太さの点を表示します
- 三角関数 sin(),cos() に与える値はラジアン(弧度法)なので、radians() で変換しています
- for (var t=0; t<360; t+=360/maxt) ・・・;
t の値を 0°から360°まで、360/maxt°ずつ増やしながら、・・・を繰り返します
このプログラムは、子供のころよく遊んだスピログラフ®を描きます。パラメータを色々変えて楽しんでください。
3.マンデルブロ集合
マンデルブロ集合は、フラクタルの概念を提唱したマンデルブロが定義しました。点($x,y$)を
$(x,y)\mapsto (x^2-y^2+c_x,2xy+c_y)$ の計算を繰返して
発散する(原点から2以上離れる)までの計算回数(発散速度)
で色付けします。このとき定数部を$(c_x,c_y)=(x,y)$(出発点)とするのがマンデルブロ集合で、想像もできない程複雑で美しいフラクタル画像が現れます。
例えば $(0.5,0.5)\mapsto(0.5,1)\mapsto(-0.25,1.5)\mapsto(-1.6875,-0.25)\mapsto(3.285,1.344)$ ですから、($0.5,0.5$) から出発した点は $4$回で発散します。右の全体図で黒い領域は発散速度$\;0\;$で、外側に赤紫の高発散速度領域が広がっています。緑や赤い点で彩られた境界領域が複雑な振舞をする(少しずれると発散速度が著しく異なる)領域で、宝物がたくさん隠れています。
p5.jsプログラムで描画領域の中心($x_0,y_0$)とサイズ$\;s$、最大計算回数 $maxIt$、色調 $R,G,B$ を変えて、宝物をみつけましょう。
拡大縮小のアニメーションプログラムは、このプログラムを編集可能にしたものです。 mandel.setUniform('p', [-0.74364388703, 0.13182590421]); で設定される中心座標を変えて、探索してみましょう。
また、このサイトには、美しい画像が得られるパラメータ値やマンデルブロ集合の詳しい情報があり、【マンデルブロ集合描画スクリプト】はとてもよくできています。
【注】$(x,y)\mapsto(x^2-y^2+c_x,2xy+c_y)$ は、複素数計算の $x+yi\to(x+yi)^2+(c_x+c_yi)\;$を意味します。
パラメータ例
全体図:x0=0, y0=0, s=2, maxIt=50,
例1:x0=-0.74364388703, y0=0.13182590421, s=0.005, maxIt=1000,
例2:x0=-1.1929755697967157, y0=-0.16206578744951963, s=0.002, maxIt=1000,
例3:x0=0.3335437395630575, y0=0.42517525749876034, s=0.00002, maxIt=1000,
ジュリア集合は、マンデルブロ集合と同じ計算式ですが、定数部$(c_x,c_y)$を定点とし、同じく複雑で美しい画像が得られます。
このブログラムで、定数部や描画領域をいろいろ変えて楽しんでみましょう。
スクラッチなどの経験がある方にはお馴染みの概念で、描画領域中で亀(Turtle)を歩かせ線画を描きます。p5.jsに亀を追加したプログラムで遊んでみます。
亀 t は、
- var t=new Turtle($x,y,d$); 位置($x,y$)に向き$\;d\;$で誕生し
- 自分の位置(t.x,t.y)、向き t.dir、色 t.color、太さ t.weight を知っていて
- $p\;$歩く:t.walk($p$)、$p\;$飛ぶ:t.jump($p$)、$d^\circ$回る:t.turn($d$) ことができ
- 位置:t.setPos($x,y$)、向き:t.setDir($d$)、色:t.color=、太さ:t.weight= の直接設定もできます。
以下の例も、亀の誕生位置・角度(Turtle($x,y,d$))を調整しながら、試してみましょう。
四角形:for (var i=0; i<4; i++) {t.walk(100); t.turn(90);}
星形:for (var i=0; i<5; i++) {t.walk(100); t.turn(144);}
Lindenmayer により提唱されたシステムで、開始文字列と書換え規則の(全体)適用により成長する文字列を記述します。
例.開始文字列$\;A$、規則 $A\to B,\ B\to BA$ に対する導出(空白は分かり易さのために入れました)は
$A\Rightarrow B\Rightarrow BA\Rightarrow BA\,B\Rightarrow BA\,B\,BA\Rightarrow BA\,B\,BA\,BA\,B\Rightarrow \cdots$
となります。
【補足】文法との違いは、規則を列全体に一斉適用することです。このシステムは、$A\to B\;$を成熟、$B\to BA\;$を細胞分裂(生殖)と解釈すると、一番簡単な細胞(生物)集合の成長モデルになっています。第$\;n\;$ステップで導出される文字列を$\;S(n)\;$とおくと、$S(n+2)=S(n+1)S(n)\;$で、その長さ $|S(n)|\;$はフィボナッチ数列になっています(確認してみて下さい)。自然界にフィボナッチ数列がよく出現する理由かもしれません。
L-システムは、文字(の一部)をタートルへの指令と解釈することにより、様々な線画を記述できます。Kevin Roast教授のサイトでは多くの実例を楽しめますし、日本語の解説サイトもあります。Prusinkiewicz と Lindenmayer の著書The Algorithmic Beauty of Plantsは現在フリーで入手でき図版を眺めるだけでも楽しいです。
p5.jsプログラムでは文字を次のように解釈しています。L-システム(開始文字列と規則)と反復回数$\;n$、タートルの開始位置と向き、$step,\ angle$ を適当に設定して楽しんでください。
| 文字 | タートル t への指令 | 備考 |
| F | t.walk($step$) | $step\;$歩く |
| f | t.jump($step$) | $step\;$飛ぶ |
| +,- | t.turn($\pm angle$) | $\pm angle^\circ\;$左回転(反時計回り) |
| 1,2,….9 | t.weight=1,2,….9 | 太さ指定 |
| b,g,y,l | t.color='brown','green','yellowgreen','lightgreen' | 色指定。Roast教授のC0~C3 |
| [ | stack.push(Object.assign({},t)) | t(のコピー)をスタックに退避 |
| ] | t=stack.pop() | 直前の'['で退避した t を取出し、描画再開 |
| その他 | 無し | 上記以外は書換え規則用の文字 |
【補足】
- 反復回数$\;n\;$を$\;0\;$から順に増やすと成長の様子が観察できますが、増えるにつれ計算時間は異常に長くなります。$n\;$は慎重に増やして下さい
- 関数 setup() 中の描画文をコメントアウトし(//を文頭に付け)て、関数 draw() 中の描画文のコメントアウト(//)を外すと描画過程が見られます
- スタックは配列で、最後尾からのみ出し(pop)入れ(push)します。最後に入れたデータが最初に取出されるので、後入れ先出し方式と呼ばれ、計算機科学の様々な場面で使われる重要な概念です
例.星形のパラメータ
step=100, angle=144, //'F'の歩数と右'-',左'+'の回転角
L_str='b2X', n=5, //開始文字列と反復回数
Rules={'X':'F+X'},
t=new Turtle(300,300,36), //亀の出発位置と向き
例.ドラゴンカーブのパラメータ
step=4, angle=90, //'F'の歩数と右'-',左'+'の回転角
L_str='FX', n=12, //開始文字列と反復回数
Rules={'X':'X+YF+',
'Y':'-FX-Y'},
t=new Turtle(300,200,90),//亀の出発位置と向き