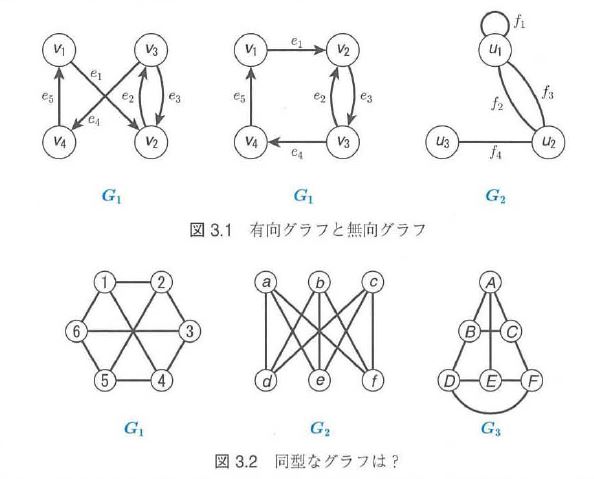
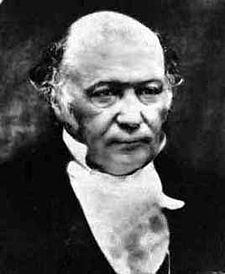グラフとは
頂点（○や□で表す）を辺で結んだもの。
有向グラフ：有向辺（→）
無向グラフ：無向辺（―）
必要に応じて、頂点や辺にラベル
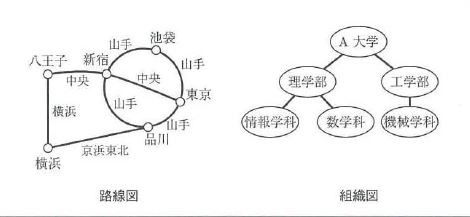
地下鉄路線図
ディズニーが描いた戦略図
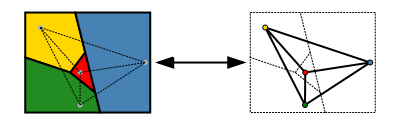
同型なグラフ
同じグラフ：頂点の位置を適当に動かすと重なる（頂点の位置は無視）
同型なグラフ：頂点の名前の付け替えで同じグラフと見なせる
パズル：$G_1$と$G_2$が同型であり、$G_3$がそれらと同形でないことを示せ。
グラフ理論の始まり
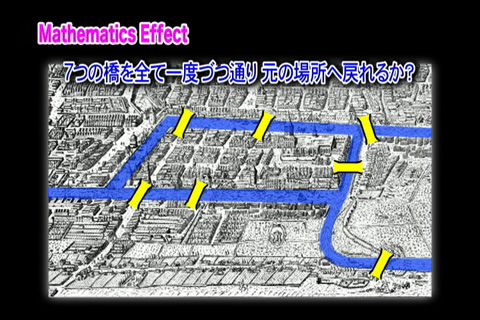
ケーニヒスベルグの橋の問題
オイラーは、グラフの一筆書きの問題に翻訳し、不可能であることを示した。
路：つながった辺の列
閉路：出発点に戻る路
オイラー路：すべての辺を1度ずつ通る路(一筆書き)
オイラー閉路：出発点に戻るオイラー路
パズル：ケーニヒスベルグの7つの橋を一度ずつ通る路はあるか。
オイラー路を持つ条件
頂点の次数：つながる辺の数
オイラー閉路がある$\iff$奇次数頂点の数が0
オイラー路がある⇔奇次数頂点の数が0または2
ケーニヒスベルグの橋のグラフは奇次数頂点の数が4
$\implies$オイラー路はない！
ハミルトン路：似て非なる問題
ハミルトンの世界一周パズル
ハミルトンは1857年に正12面体の各頂点を1度ずつ通る周遊路を求めるパズルを作成した。
ハミルトン(閉)路：
各頂点を1度ずつ通る(閉)路
パズル：右のグラフのハミルトン閉路を求めよ
ハミルトン路には、オイラー路のような簡明な判定法がなく、虱潰しの試行錯誤しかないと(信じられている)
どうしてそんなことが言えるのか？？
平面グラフ
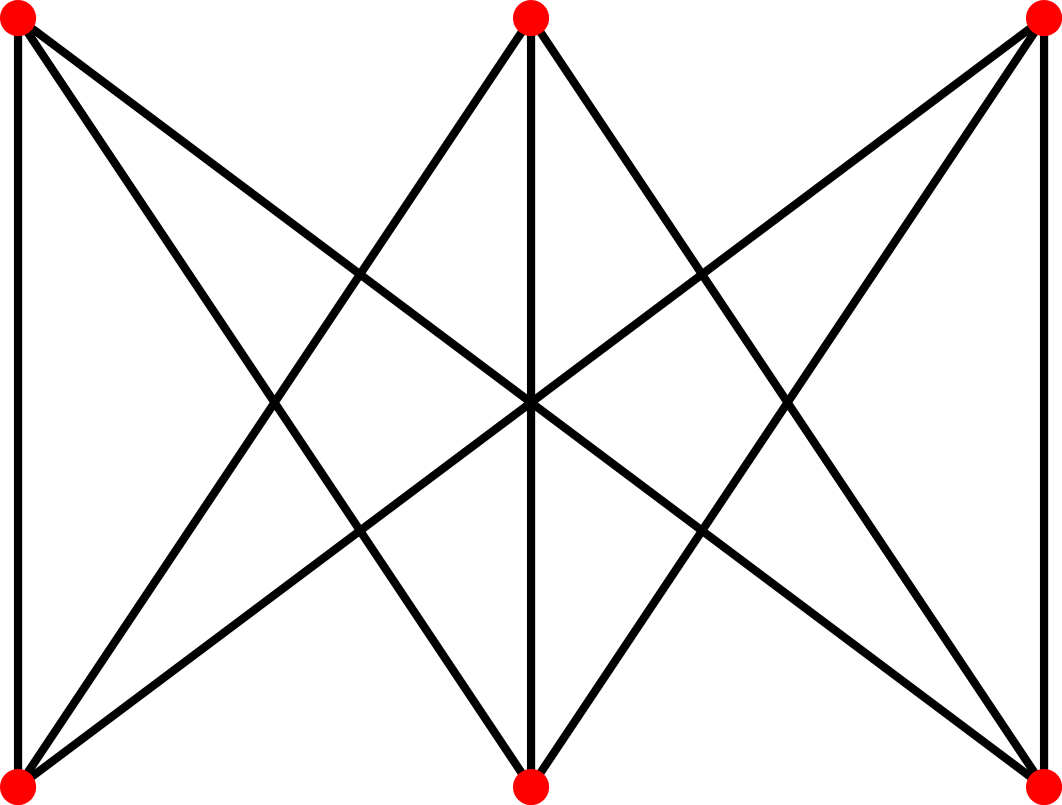
頂点や辺をうまく配置すれば、辺が交差しないグラフ$K_n$：頂点数$n$の完全グラフ(すべての頂点間に辺があるグラフ)
2部グラフ：頂点が2分割され、同一グループ内には辺がないグラフ
$K_{m,n}$:頂点数が$m$と$n$の2部グラフ
パズル：$K_4$と$K_{2,3}$を辺が交差しないように描け。
オイラーの公式
定理．平面上に辺が交差しないように描かれたグラフでは$領域数＋頂点数－辺の数=2$
略証．グラフに辺や頂点を追加しても、定理の式は保存される。
定理．$K_5$と$K_{3,3}$は平面グラフではない。
略証．$K_5$では、$頂点数=5$、$辺の数={}_5\mathrm{C}_2=10$、辺が交差しなければ$領域数={}_5\mathrm{C}_3=10$なので、定理より平面グラフではない。
$K_{3,3}$では、$頂点数=6$、$辺の数=3×3=9$、辺が交差しなければ定理より$領域数=2+9-6=5$。そのためには$5×4/2=10$本の辺が必要で、平面グラフではない。
パズル：2部平面グラフで5個の領域を構成するためには少なくとも10本の辺が必要であることを示せ。
クラトフスキーの定理
定理 グラフが平面グラフである必要十分条件は、$K_5$と$K_{3,3}$を同相な部分グラフとして持たないことである。ここで、二つのグラフが同相であるというのは、辺の途中に頂点を挿入する操作あるいはその逆操作で一方から他方(と同形なグラフ)に移ることをいう。
４色定理
平面グラフの塗分け問題：平面グラフ(地図)の各領域(各国)の塗り分ける問題。ただし辺(国境)を共有する領域(国)を同じ色で塗ってはいけない。
平面グラフの頂点彩色問題：隣あう頂点を異なる色で塗り分ける問題。
これらの問題は、領域⇔頂点、辺を共有⇔辺で結ぶ、ことによって互いに移りあう(双対な平面グラフ)。
「すべての平面グラフが４色塗分け(彩色)可能か」は長い間未解決であったが、1976年にアッペルとハーケンが4色で十分であることをコンピュータを駆使して証明した。当時は、手作業による検証が不可能なこの証明を疑問視する声もあった。
パズル：4色に塗り分けてみよう。
www.tamentaico.com/four/
３彩色問題
与えれたグラフが3彩色可能か否か判定する問題。ハミルトン(閉)路問題と同様に、虱潰しの試行錯誤よりうまい方法はないと信じられている。