有限オートマトン
辺にラベルの付いた有向グラフ
頂点⇒状態、 ラベルaがついた有向辺⇒(イベント)aによる遷移
開始状態(→)と、受理状態(◎、複数可)が指定される
ラベルには、空列$\varepsilon$も許す(イベントなしの遷移)
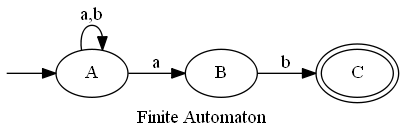
有限オートマトンは、開始状態から受理状態へ至る路の
ラベル列を受理する。
ラベル列の集合を認識(受理)する。
定理．有限オートマトンで認識される文字列集合は、正規集合である。
農夫パズル
オオカミ($W$)とヤギ($G$)を連れキャベツの籠($C$)を持った農夫($F$)が小舟で川を渡りたい。
- 小舟には農夫の他一匹(一籠)しか乗せられない
- 農夫がいないとオオカミはヤギを食べてしまう
- 農夫がいないとヤギはキャベツを食べてしまう
状態：両岸にいる(ある)ものの配置
遷移：農夫が小舟で運ぶもの $W, G, C$。なければ $F$
パズル．農法パズルの解を示せ。
決定性有限オートマトン
辺のラベルの集合を$\Sigma$とする。有限オートマトンは次の条件を満たすとき決定性であるという。
- 開始状態が1つ
- すべての状態とラベルの組に対して、遷移先の状態が1つ
決定性有限オートマトンでは、
開始状態から与えられたラベル列を持つ路は唯一つ(ある)
ラベル列は、到達先の状態が受理状態なら受理される
(非決定性)有限オートマトンでは、
開始状態から与えられたラベル列を持つ路は複数(または0個ある)
ラベル列は、到達可能な状態の中に受理状態があれば受理される
決定性有限オートマトンへの変換
定理．有限オートマトンで認識可能$\implies$決定性オートマトンでも認識可能略証．決定性オートマトンを次のように作る。
- ラベル列$w$で到達する状態は、もとの(非決定性)オートマトンで$w$で到達可能な状態の集合
- 開始状態はもとの開始状態から$\varepsilon$で到達可能な状態の集合
- 受理状態はもとの受理状態を含む集合
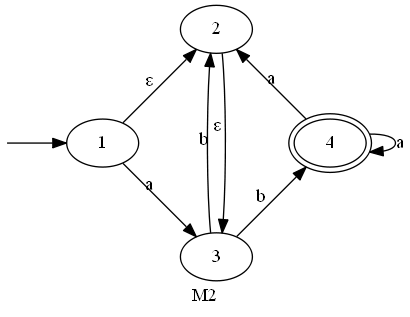
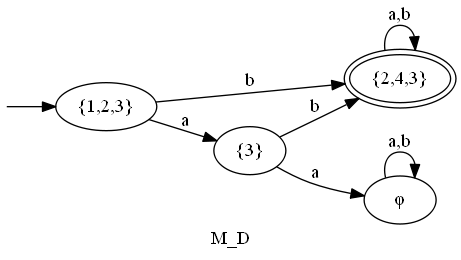
文字列集合の方程式
$A,B$を文字列集合とし、方程式 $X=AX\cup B$ を考えると$X=A^*B$は、(包含関係で最少の)解である。
$ε\not\in A$ ならば、$X=A^*B$ は唯一つの解である。
略証．$A(A^*B)\cup B=B\cup A(A^0\cup A^1\cup \cdots)B=(A^0\cup A^1\cup \cdots)B=A^*B$
有限オートマトンが認識する正規集合の求め方：
有限オートマトンの状態$q$に対し、$q$を開始状態とする有限オートマトンが受理する集合を$X_q$とおいて立てた方程式を解く。
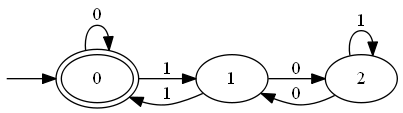(1) $X_0=0X_0\cup 1X_1\cup \varepsilon$(2) $X_1=1X_0\cup 0X_2$
(3) $X_2=1X_2\cup 0X_1$
(3)より$X_2=1^*0X_1$。(2)に代入して$X_1=1X_0\cup 01^*0X_1=(01^*0)^*1X_0$。
(1)に代入して$X_0=0X_0\cup 1(01^*0)^*1X_0\cup\varepsilon=(0∪1(01^*0)^*1)^*$。
正規集合⇒有限オートマトン
次の手順で有限オートマトンを構成する。- 与えられた文字列を受理する有限オートマトンを作る
- 2つの有限オートマトンから、それらが認識する文字列集合の連接を認識する有限オートマトンを作る
- 2つの有限オートマトンから、それらが認識する文字列集合の和集合を認識する有限オートマトンを作る
- 有限オートマトンから、それが認識する文字列集合の閉包を認識する有限オートマトンを作る
パズル：$(a\cup b^*c)^*c$を認識する有限オートマトンを示せ。
ヒント：有限オートマトンは開始状態と受理状態がそれぞれ1つで、開始状態への遷移と、受理状態からの遷移はないものを考えよう。
有限オートマトンと正規集合
定理．次の条件は同値$\implies$正規集合- 有限オートマトンで受理される
- 決定性有限オートマトンで受理される
- 正規表現で表される
定理．$A,B$が$\Sigma$上の正規集合ならば、$A\cup B, A\cap B, \Sigma^*-A$も正規集合である。
略証．$A\cup B$も正規集合なのは明らか。$A$を認識する決定性有限オートマトンの受理状態と非受理状態を入れ替えた決定性有限オートマトンは$\Sigma^*-A$を認識する（$\Sigma^*$は$\Sigma$上の文字列の全体を表す）。
パズル．文字列の集合$A$に対し、$A^R$を$A$の文字列を逆順にした文字列の集合とする。$A$が正規集合なら$A^R$も正規集合であることを示せ。
正規表現の記法
計算機システムで使われる正規表現の基本演算は次の３種類| 記法 | 説明 | ||||||||||||||||||||||||||
| 連接 | 正規表現を続けて書けば、それらを続けた文字列と合致 | ||||||||||||||||||||||||||
| | | 和(または)。どちらかのパターンと合致すれば合致。 | ||||||||||||||||||||||||||
| * | 直前の文字(文字列)の0回以上の繰り返しと合致 |
| 記法 | 説明 | 使用例 |
| + | 1回以上の繰り返し | 12+ → 12、122、・・・ と合致 12+＝122* |
| ? | 0,1回の繰り返し | 12? → 1、12 と合致 12?＝1|12 |
| {n} | n回繰り返し | (ab){3} → abababに合致 |
| {n, } | n回以上繰り返し | a{3,} →aaa、aaaa、…に合致 |
| {m,n} | m～n回繰り返し | a{3,5} →aaa、aaaa、aaaaaに合致 |
正規表現の記法
(３)文字の集合：1文字指定する| 記法 | 説明 | 使用例 |
| . | 改行文字を除く任意の1文字 | windows.. windowsの後に2文字続く文字列と合致 |
| [ ] | [ ] 内に並べた文字のどれか | [ab]＝a|b |
| - | 文字の区間。[ ] 内で用いる | [a-z]＝a|b|・・・|z a-zの小文字アルファベット全て [0-9]＝0|1|・・・|9 全角の数字 [0-9A-Z] 大文字のアルファベットか数字 |
| ^ | 否定。[ ] 内で用いる | [^a-z] 小文字のアルファベット以外全て |
12+ →1222222222 に対し10桁目の1222222222までと合致
12+? →1222222222 に対し2桁目の12までと合致
正規表現の記法
(４)特殊な意味を持つ文字| 記法 | 説明 | 使用例 |
| ^ | 行頭 | ^abc →行頭にある abc と合致 |
| $ | 行末 | abc$ →行末にある abc と合致 |
|
|
正規表現による検索と置換
正規表現において$n$番目の括弧対で括られた部分に合致した文字列は、$\$n$ で表せるので、置換に利用できる。右はJava Scriptで実装した正規表現による検索・置換機能である。検索文字列や置換文字列を指定して[検索]、[置換]を押すと結果が下の欄に表示される。
パズル．1～4の正規表現を求めて検索してみよう。
- 3桁の数字
- 3000未満の非負整数
- aで始まりaで終わる6文字以下の英小文字列
- 数字０～９で始まり句点。で終わる文
- 英字の姓と名を入れ替えてみよう
正規表現による英文分析
正規表現による検索を用いると、例えば英語の学習に役立つばかりでなく、文書・文献の特徴を数量的に抽出し、著者の異同や時代の推定、思想と文体との関係等を分析することも可能になる。その意味で、正規表現検索は文体の処理・解析のための重要なツールになっている。パズル．正規表現検索を用いた英文分析
- 秋田大学のSCORP検索では、正規表現検索を応用して、電子的に保存されている英文の解析を行うことができる。このページを表示させよう。
- Search Word欄に \s(for|in|on|to|with)\s[a-z]+ing\s(for|in|of|on|to|with)\s を入れてみよう。また、これが何を意味するか考えてみよう。
- 適当な動詞(過去、過去分詞、三単元を含む)の出現数を調べてみよう。