コンピュータの原理

５大機能と構成装置

コンピュータは、(記憶されている)プログラムの指示にしたがって、入力されたデータを記憶し、記憶したデータについて演算を行い、求める結果を出力する。また、これら一連の処理が正しく行われるように制御する。


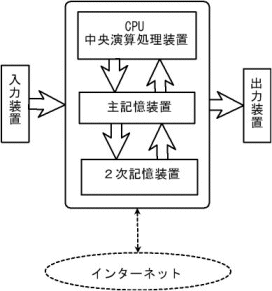
演算機能：CPU(演算装置)
制御機能：CPU(制御装置)
記憶機能：主記憶装置、補助記憶装置
入力機能：入力装置
出力機能：出力装置
(通信機能：通信装置)

入力装置と出力装置

入力装置：外部からデータを取り込む装置
　人間が理解しやすい数字・文字・画像・音声を
　コンピュータが理解できる0,1列に変換して主記憶装置に送る
 文字入力装置：キーボード
ポインティングデバイス：マウス、タッチパネル・スクリーン
音声入力装置：マイク
図形入力装置：イメージスキャナ、デジタル(ビデオ)カメラ、ディジタイザ
カード読み取り装置：磁気カード、ICカードなどの読み取り装置
パターン認識装置：OCR、OMR、バーコードリーダー

出力装置：処理結果を外部に取り出す装置
　主記憶内の処理結果(0,1列)を
　人間が理解しやすい数字・文字・画像・音声に変換して表示する
 デスプレイ：液晶ディスプレイ
音声出力装置：スピーカー
プリンタ：インクジェットプリンタ、レーザープリンタ
プロッタ：XYプロッタ

記憶装置とその使い分け

主記憶装置外部(補助)記憶装置
高速低速
高価⇔小容量安価⇔大容量
揮発性不揮発性
移・増設困難移・増設可能
SRAM、DRAMHDD,USBメモリ,CD,DVD,…

揮発性：電源OFFともに記憶内容が失われる

主記憶装置：高速・揮発性のため計算時の一時的格納に用いる
外部記憶装置：大容量・不揮発性のため長期的に保存に用いる

プログラムやデータは通常、外部記憶装置に保持され、
  1. 主記憶装置にロードされてから、
  2. 主記憶装置とCPUの間で処理・計算が行われ、
  3. 結果は再び、外部記憶装置にセーブされる

パズル．２種類の記憶装置の使い分けとその理由を考えよ。

主記憶装置

1バイトごとにアドレス(番地)　高速、高価(小容量)、揮発性

RAM(Random Access Memory)
：アドレス選択回路で場所を見つけ、読み書き回路で読み書き

ア
ド
レ
ス
選
択
回
路		 ⇒
番地内容
0000000000000000
0000000100010010
0000001000000110
　・
　・
　・		　・
　・
　・
⇒ 読
み
書
き
回
路

DRAM：低速・安価、主記憶用、SRAM：高速・高価、キャッシュメモリ用

外部記憶装置(HDD)

HDD：低速、安価(大容量)、不揮発性

　高速回転する磁気ディスク上のデータを、
　アクセスアームの先の磁気ヘッドで読み書き

ディスクは円周状のトラックに分かれ
トラックは放射状のセクタに分かれる

アクセス時間=シーク時間+サーチ時間+転送時間
　　シーク：ヘッドがトラック上に移動
　　サーチ：セクタがヘッド下に移動
　　転送：ヘッドによる読み書き

記憶装置の階層

アクセス時間容量
レジスタCPU1～10n秒～1KB
↓数倍↓約千倍
キャッシュメモリSRAM2～50n秒10K～4MB
↓約十倍↓約千倍
主記憶DRAM50～300n秒200M～2GB
↓数百倍↓数百倍
外部記憶HDD10～100m秒200G～1TB

キャッシュメモリ　
CPUと主記憶の間にあって、その速度差を埋める
主記憶にアクセス→塊をキャッシュメモリに格納
→以後キャッシュメモリにアクセス(なけれ主記憶にアクセス)
キャッシュメモリが満杯のときは、古いデータを主記憶に戻す
　FIFO：格納時期が最も古いデータを戻す
　LRU ：使用時期が最も古いデータを戻す

中央処理装置

コンピュータの頭脳：演算・制御を行う
CPU(コンピュータ)の基本動作サイクル
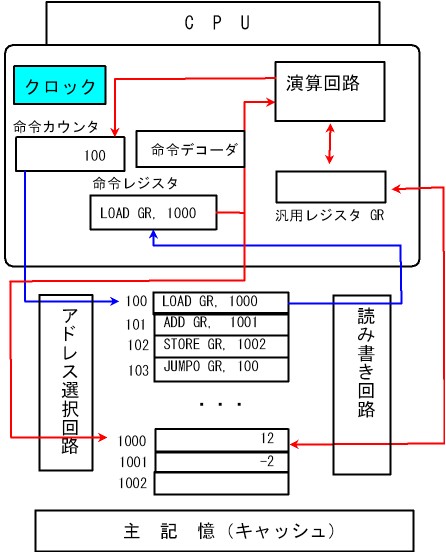
  1. プログラムカウンタの値(番地)を読み取る
  2. その番地にあるデータ(命令)を命令レジスタに移す
  3. プログラムカウンタの値を１(命令サイズ分)増やす
  4. 命令デコーダが命令レジスタ中の命令を解釈する
  5. 演算装置等が解釈された命令を実行する

CPU内の記憶領域（レジスタ)
　プログラムカウンタ：命令番地を格納
　命令レジスタ：命令を格納
　汎用レジスタ(GR)：
　　演算に用いるデータを格納(通常複数)

機械語とアセンブリ言語

機械語：命令を0,1の列で表現、CPUが直接実行できる
アセンブリ言語：人に分かりやすく機械語命令を文字で表現
　　機械語と原則１対１に対応、アセンブラが機械語に翻訳
命令の種類
  1. ロード命令
    LD GR $n$：$n$番地のデータをGR(汎用レジスタ)に移せ
  2. ストア命令
    ST GR $n$：GRのデータを$n$番地に移せ
  3. 演算命令
    ADD GR $n$：GRに$n$番地のデータを加えよ
    MUL GR $n$：GRに$n$番地のデータを掛けろ
    ・・・
  4. ジャンプ命令
    JP0 GR $m$：GRの値が$0$だったら$m$番地(の命令)に飛べ
    ・・・
  5. 入力命令、出力命令

数式→アセンブリ言語

$x$: 1200番地、$y$: 1201番地、$z$: 1202番地、$w$:1203番地とする。
以下の式を計算するアセンブリプログラムは、
$z＝x+y$
LD GR 1200, ADD GR 1201, ST GR 1202
　($x$ に　　$y$ を足して　　$z$ に代入)
$w＝x\times y+z$
LD GR 1200, MUL GR 1201, ADD GR 1202, ST GR 1203
　($x$　に　　$y$ を掛け　　　$z$を足して　　$w$ に代入)
$w＝z-x\times y$
LD GR 1200, MUL GR 1201, ST GR 1204
　($x$　に　　$y$ を掛け　　1204番地に格納し
LD GR 1202, SUB GR 1204, ST GR 1203
　$z$ から　　1204番地を引いて $w$ に代入)

数式→アセンブリ言語の問題

$x$: 1200番地、$y$: 1201番地、$z$: 1202番地、$w$: 1203番地とする

パズル．以下の数式をアセンブリ言語に変換せよ
１)$z＝x-y$
２)$w＝x+y\times z$
３)$w＝x\times (y+z)$

複雑な数式をアセンブリ言語で書くのは困難
→プログラム中で数式を使えるようにしたい
→FORTRAN(FORmula TRANslator)の開発

演算(電子)回路

xyx∧yx∨yx￢x
000001
010110
1001
1111
演算装置：汎用レジスタ＋演算回路
演算回路への入出力は0,1の列(32ビット)
⇒AND(∧)、OR(∨)、NOT(￢)素子(右表)の組み合わせで実現


半加算器(x＋y)の設計
xy x＋yその行だけ1の論理式
上桁下桁
0000￢x∧￢y
0101￢x∧y
1001x∧￢y
1110x∧y
論理式x∧y(￢x∧y)∨(x∧￢y)




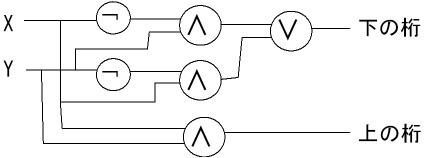
出力が1の行に対応する論理式を∨で結ぶ

論理式の真理値表
右の欄に変数 x, y, z, w を用いた論理式を入れて[評価]を押すと、その真理値表が得られる。ただし ∧は&、∨は|、￢は!で表す。

パズル．次の論理式の真理値表を求めよ
1) x∧y
2) ￢x∧y
3) x∧￢y
4) (￢x∧y)∨(x∧￢y)

加算回路

xyc x＋y＋cその行だけ1の論理式
上の桁下の桁
00000￢x∧￢y∧￢c
00101￢x∧￢y∧c
01001￢x∧y∧￢c
01110￢x∧y∧c
10001x∧￢y∧￢c
10110￢x∧￢y∧c
11010x∧y∧￢c
11111x∧y∧c
論理式
複数桁(32桁)の加算器は
1桁目は半加算器(x＋y)
以降は全加算器(x＋y＋c)
をつなげる 
      ０ １ ０ １　ｘ
 ＋）1１1１0０1１　ｙc
   １ ０ ０ １ ０

全加算器(x＋y＋c)の設計

下の桁＝(￢x∧￢y∧c)∨(￢x∧y∧￢c)∨(x∧￢y∧￢c)∨(x∧y∧c)
パズル．上の桁を表す論理式を求めよ

スィッチング素子

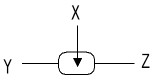xのon/offでy-z間が切断/接続
リレー、真空管、トランジスタ(半導体)で実現

スイッチング素子だけで任意の演算回路を組み立てられる
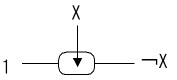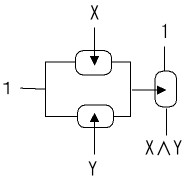￢回路∧回路パズル．∨回路を描け
∧、∨、￢の素子を作れればよい(右図)
スイッチング素子を格子状並べて、配線を工夫すれば任意の回路が作れる

集積回路
半導体基板の上に光学写真技術によって微細な素子や配線などの像を焼付け、その像を保護マスクとして半導体基板の溶融・上塗りを繰り返して、回路を作成する。
写真(回路図)を細かくできればできるほど、集積度があがる。

End Page

End Page